24.2.2 直线与圆的位置关系(第二课时)[上学期]
文档属性
| 名称 | 24.2.2 直线与圆的位置关系(第二课时)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 122.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-09-24 00:00:00 | ||
图片预览



文档简介
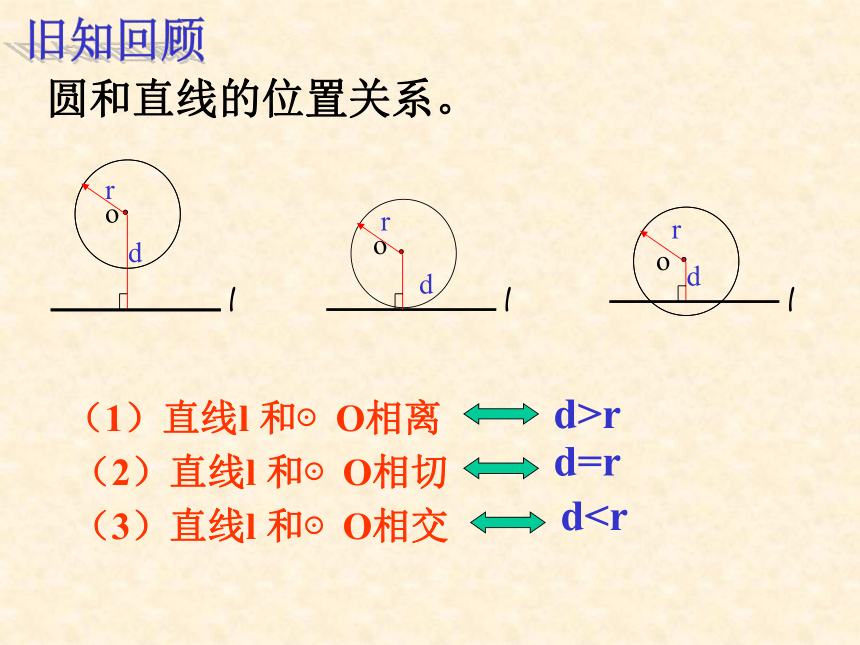
课件12张PPT。24.2.2 直线与圆的位置关系(2)(2)直线l 和⊙O相切圆和直线的位置关系。 (1)直线l 和⊙O相离(3)直线l 和⊙O相交d>rd=rd1.⊙O的半径为3 ,圆心O到直线l的距离为d,若直线l
与⊙O没有公共点,则d为( ):
A.d >3 B.d<3 C.d ≤3 D.d =3
2.圆心O到直线的距离等于⊙O的半径,则直线
和⊙O的位置 关系是( ):
A.相离 B.相交 C.相切 D.相切或相交
3.判断:若直线和圆相切,则该直线和圆一定有一个公共点.( )
4.等边三角形ABC的边长为2,则以A为圆心,半径为1.73的圆
与直线BC的位置关系是 ,以A为圆心,
为半径的圆与直线BC相切.AC√相离5、已知点A的坐标为(1,2),⊙A的半径为3.
(1)若要使⊙A与y轴相切,则要把⊙A向右平移几个单位?此时,⊙A与x轴、⊙A与点O分别有怎样的位置关系?若把⊙A向左平移呢?(2)若要使⊙A与x轴、y轴都相切,则圆心A应当移到 什么位置?请写出点A所有可能位置的坐标.
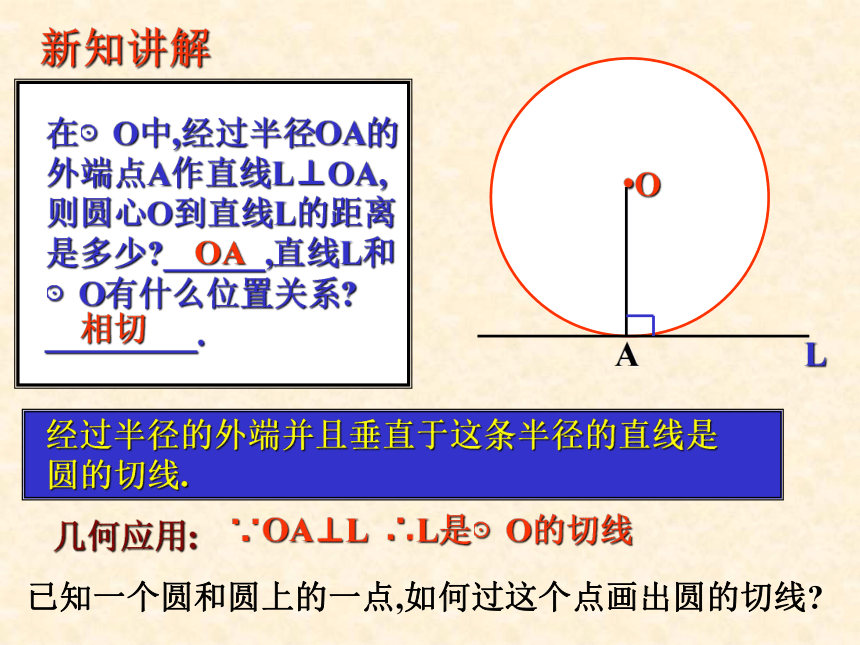
在⊙O中,经过半径OA的
外端点A作直线L⊥OA,
则圆心O到直线L的距离
是多少?______,直线L和
⊙O有什么位置关系?
_________.新知讲解.OAOA相切L经过半径的外端并且垂直于这条半径的直线是
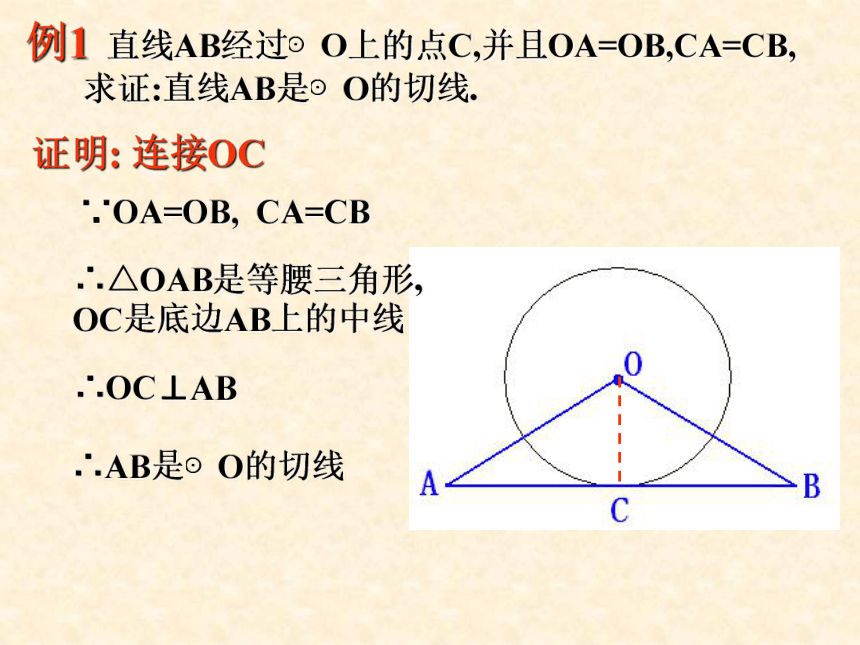
圆的切线.几何应用: ∵OA⊥L ∴L是⊙O的切线已知一个圆和圆上的一点,如何过这个点画出圆的切线?例1 直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
求证:直线AB是⊙O的切线.证明: 连接OC∵OA=OB, CA=CB∴△OAB是等腰三角形,
OC是底边AB上的中线
∴OC⊥AB∴AB是⊙O的切线练习1 如图,AB是⊙O的直径,点D在AB的延长线 上,BD=OB,点C在圆上,∠CAB=300.
求证:DC是⊙O的切线.方法引导
当已知直线与圆有公共点,要证明直线与圆相切时,可先连结圆心与公共点,再证明连线垂直于直线 ,这是证明切线的一种方法.2.AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E
作⊙O的切线交AC于点D,试判断△AED的形状,并
说明理由.3.在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,以D为
圆心,DB长为半径作⊙D.试说明:AC是⊙D的切线.FE1、定义法:和圆有且只有一个公共点的直线是圆的切线。
2、数量法(d=r):和圆心距离等于半径的直线是圆的切线。
3、判定定理:经过半径外端且垂直于这条半径的直线是圆的切线。证明直线与圆相切有如下三种途径:即:若直线与圆的一个公共点已指明,则连接这点和圆心,说明直线垂直于经过这点的半径;若直线与圆的公共点未指明,则过圆心作直线的垂线段,然后说明这条线段的长等于圆的半径..OAL思考将上页思考中的问题
反过来,如果L是⊙O
的切线,切点为A,那么
半径OA与直线L是不
是一定垂直呢?一定垂直切线的性质定理:圆的切线垂直于过切点的半径练习 P103. 1. 21、切线和圆只有一个公共点。2、切线和圆心的距离等于半径。3、切线垂直于过切点的半径。4、经过圆心垂直于切线的直线必过切点。5、经过切点垂直于切线的直线必过圆心。切线的性质:切线的性质3、4、5可归纳为:已知直线满足a、过圆心,b、过切点,c、垂直于切线中任意两个,便得到第三个结论。
与⊙O没有公共点,则d为( ):
A.d >3 B.d<3 C.d ≤3 D.d =3
2.圆心O到直线的距离等于⊙O的半径,则直线
和⊙O的位置 关系是( ):
A.相离 B.相交 C.相切 D.相切或相交
3.判断:若直线和圆相切,则该直线和圆一定有一个公共点.( )
4.等边三角形ABC的边长为2,则以A为圆心,半径为1.73的圆
与直线BC的位置关系是 ,以A为圆心,
为半径的圆与直线BC相切.AC√相离5、已知点A的坐标为(1,2),⊙A的半径为3.
(1)若要使⊙A与y轴相切,则要把⊙A向右平移几个单位?此时,⊙A与x轴、⊙A与点O分别有怎样的位置关系?若把⊙A向左平移呢?(2)若要使⊙A与x轴、y轴都相切,则圆心A应当移到 什么位置?请写出点A所有可能位置的坐标.
在⊙O中,经过半径OA的
外端点A作直线L⊥OA,
则圆心O到直线L的距离
是多少?______,直线L和
⊙O有什么位置关系?
_________.新知讲解.OAOA相切L经过半径的外端并且垂直于这条半径的直线是
圆的切线.几何应用: ∵OA⊥L ∴L是⊙O的切线已知一个圆和圆上的一点,如何过这个点画出圆的切线?例1 直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
求证:直线AB是⊙O的切线.证明: 连接OC∵OA=OB, CA=CB∴△OAB是等腰三角形,
OC是底边AB上的中线
∴OC⊥AB∴AB是⊙O的切线练习1 如图,AB是⊙O的直径,点D在AB的延长线 上,BD=OB,点C在圆上,∠CAB=300.
求证:DC是⊙O的切线.方法引导
当已知直线与圆有公共点,要证明直线与圆相切时,可先连结圆心与公共点,再证明连线垂直于直线 ,这是证明切线的一种方法.2.AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E
作⊙O的切线交AC于点D,试判断△AED的形状,并
说明理由.3.在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,以D为
圆心,DB长为半径作⊙D.试说明:AC是⊙D的切线.FE1、定义法:和圆有且只有一个公共点的直线是圆的切线。
2、数量法(d=r):和圆心距离等于半径的直线是圆的切线。
3、判定定理:经过半径外端且垂直于这条半径的直线是圆的切线。证明直线与圆相切有如下三种途径:即:若直线与圆的一个公共点已指明,则连接这点和圆心,说明直线垂直于经过这点的半径;若直线与圆的公共点未指明,则过圆心作直线的垂线段,然后说明这条线段的长等于圆的半径..OAL思考将上页思考中的问题
反过来,如果L是⊙O
的切线,切点为A,那么
半径OA与直线L是不
是一定垂直呢?一定垂直切线的性质定理:圆的切线垂直于过切点的半径练习 P103. 1. 21、切线和圆只有一个公共点。2、切线和圆心的距离等于半径。3、切线垂直于过切点的半径。4、经过圆心垂直于切线的直线必过切点。5、经过切点垂直于切线的直线必过圆心。切线的性质:切线的性质3、4、5可归纳为:已知直线满足a、过圆心,b、过切点,c、垂直于切线中任意两个,便得到第三个结论。
同课章节目录
