24.1.4圆周角[上学期]
文档属性
| 名称 | 24.1.4圆周角[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 420.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-09-13 20:20:00 | ||
图片预览

文档简介
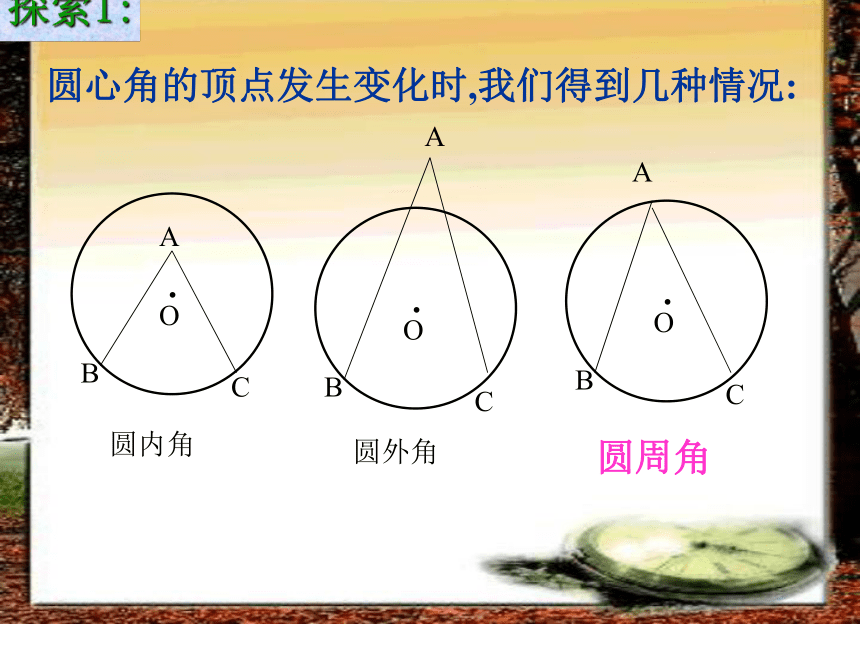
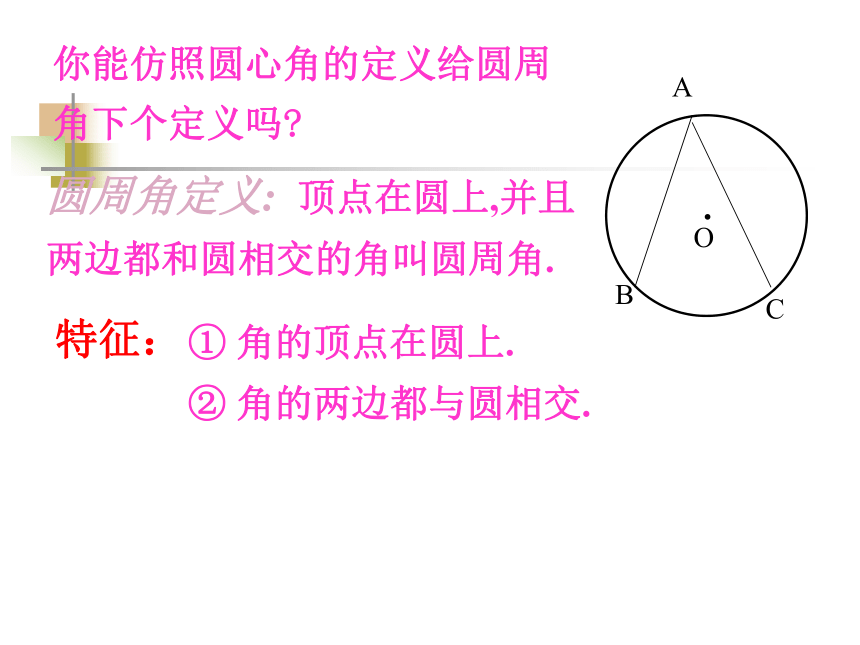
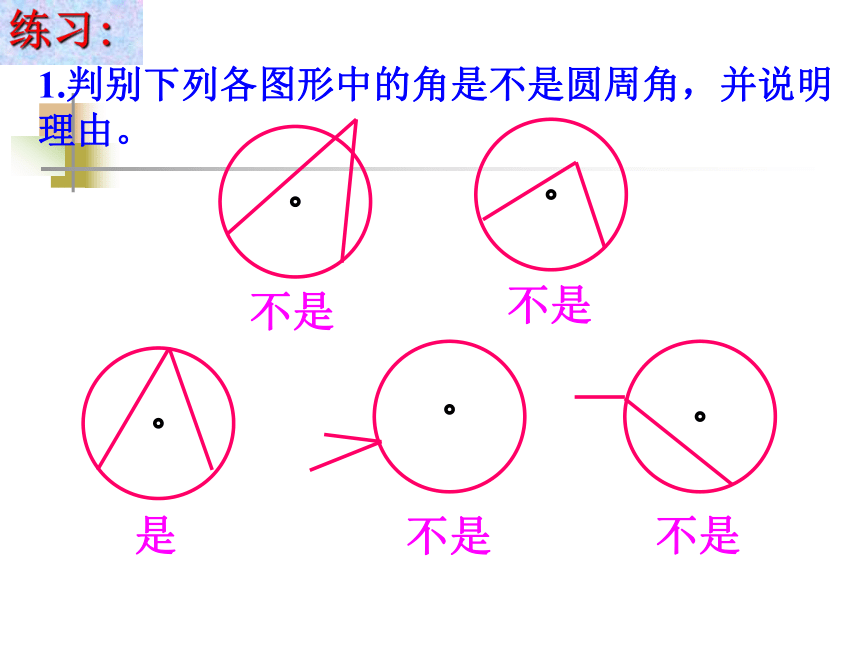
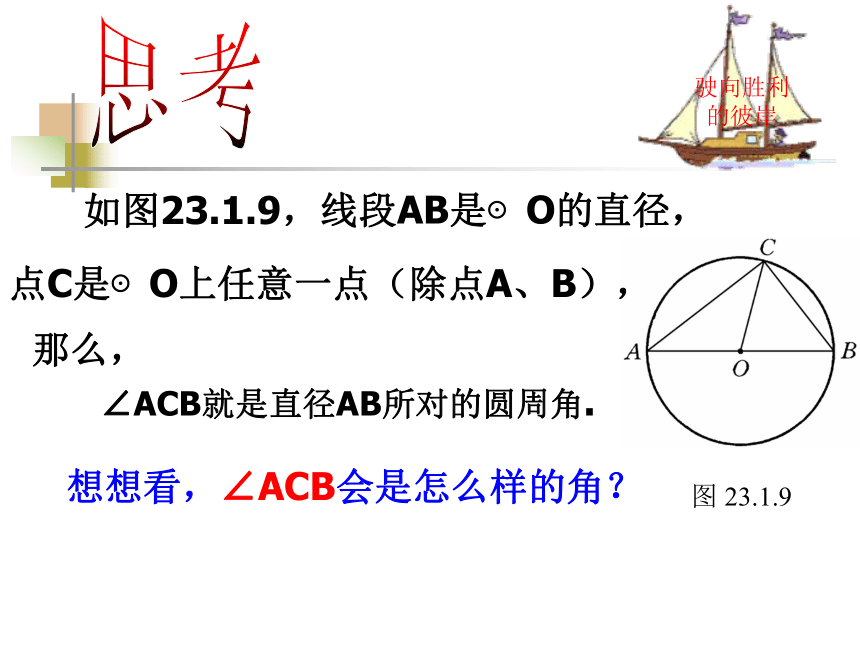
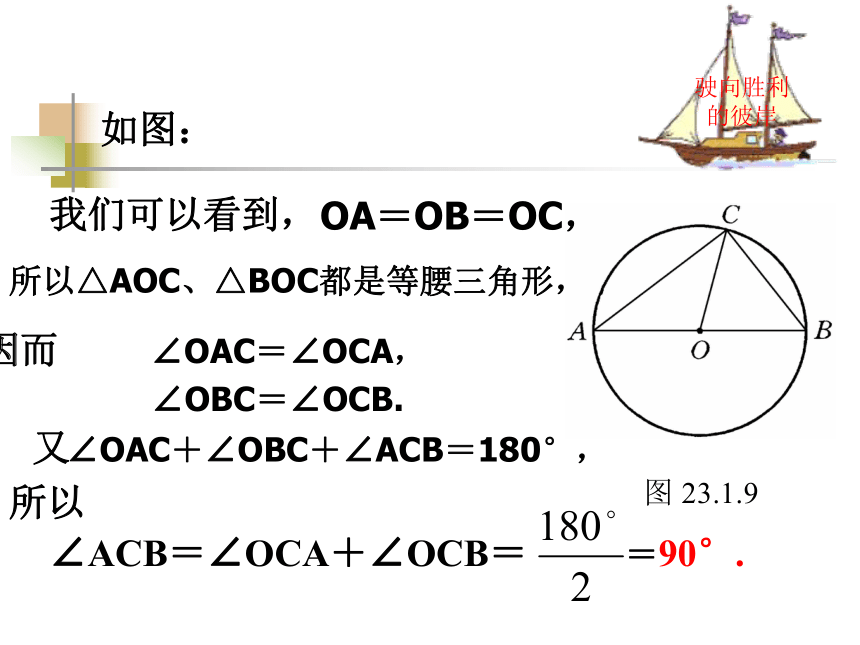
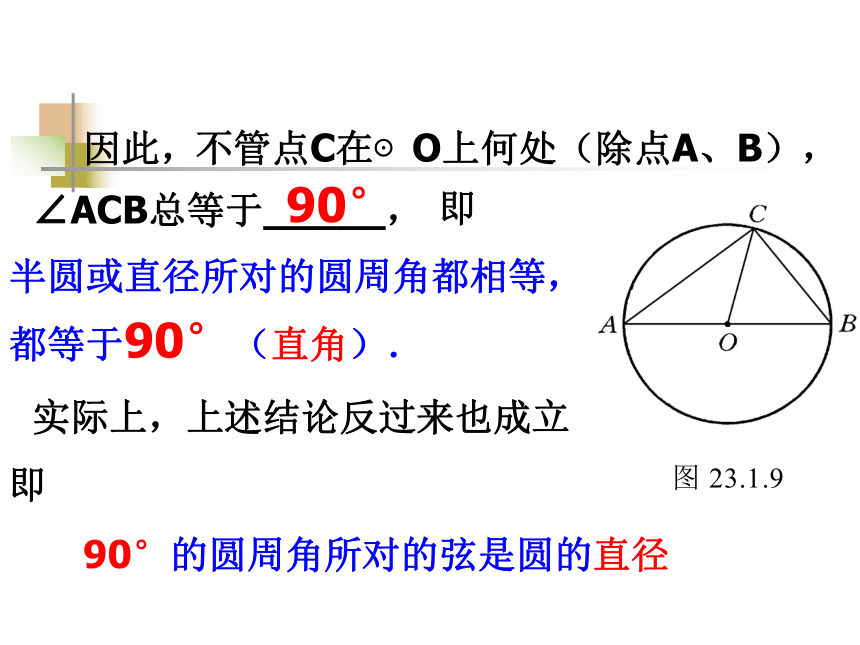
课件19张PPT。一. 复习引入:1.圆心角的定义?在同圆(或等圆)中,如果圆心角、弧、弦有一组量相等,那么它们所对应的其余两个量都分别相等。答:顶点在圆心的角叫圆心角2.上节课我们学习了一个反映圆心角、弧、弦三个量之间关系的一个结论,这个结论是什么?圆心角的顶点发生变化时,我们得到几种情况:A.OBCAA圆内角圆外角圆周角探索1:你能仿照圆心角的定义给圆周角下个定义吗?圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角.特征:1.判别下列各图形中的角是不是圆周角,并说明理由。不是不是是不是不是练习:驶向胜利的彼岸思考如图23.1.9, 线段AB是⊙O的直径, 点C是⊙O上任意一点(除点A、B), 那么, ∠ACB就是直径AB所对的圆周角. 想想看,∠ACB会是怎么样的角? 驶向胜利的彼岸我们可以看到, OA=OB=OC, 所以△AOC、△BOC都是等腰三角形, 因而∠OAC=∠OCA, ∠OBC=∠OCB.又 ∠OAC+∠OBC+∠ACB=180°,所以 ∠ACB=∠OCA+∠OCB==90°. 如图:因此, 不管点C在⊙O上何处(除点A、B), ∠ACB总等于_____, 90° 即半圆或直径所对的圆周角都相等, 都等于90°(直角). 实际上,上述结论反过来也成立
即90°的圆周角所对的弦是圆的直径 那么对于一般的圆周角,又有什么规律呢? 如图23.1.10, ∠ACB、 ∠ADB都是弧AB所对的圆周角. ∠AOB是弧AB所对的圆心角. 这几个角有什么关系呢?
试一试(1) 分别量一量图23.1.10中弧AB所对的两个圆周角的度数,比较一下. 再变动点C在圆周上的位置,看看圆周角的度数有没有变化. 你发现其中有什么规律吗?
(2) 分别量出图23.1.10中弧AB所对的圆周角和圆心角的度数,比较一下,你发现了什么规律?
我们可以发现: 圆周角的度数没有变化. 并且 圆周角的度数恰好为同弧所对的圆心角的度数的一半.
由上述操作可以猜想: 在一个圆中,一条弧所对的任意一个圆周角的大小都等于该弧所对的圆心角的一半.
为了验证这个猜想, 如图23.1.11所示, 可将圆对折,使折痕经过圆心O和圆周角的顶点C,这时可能出现三种情况: (1) 折痕是圆周角的一条边, (2) 折痕在圆周角的内部, (3) 折痕在圆周角的外部. 我们来分析一下第一种情况: 如图23.1.11(1), 由于OA=OC,因此 ∠A=∠C,
而∠AOB是△OAC的外角, 所以∠C=∠AOB.对(2)、(3),有同样的结论.
由此,可以得出: 【一条弧所对的圆周角等于该弧所对的圆心角的一半】. 因此我们可以知道:【在同圆(或等圆)中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半; 相等的圆周角所对的弧相等】.
三、应用举例解 例2 如图23.1.12,AB是⊙O的直径,∠A=80°.求∠ABC的度数.因为AB是⊙O的直径,而直径所对的圆周角是直角,所以 ∠ABC=180°-∠A-∠ACB
=180°-80°-90°
=10° 驶向胜利的彼岸四、课堂练习试找出图中所有相等的圆周角.2.在圆中,一条弧所对的圆心角和圆周角分别为(2x+100)°和(5x-30)°,求这条弧所对的圆心角和圆周角的度数.
练习:130°1.AB、AC为⊙O的两条弦,延长CA到D,使 AD=AB,如果∠ADB=35° ,
求∠BOC的度数。∠BOC =140° ∠A=21° 五.课堂小结1. 【圆周角的定义】 顶点在圆上,两边都与圆相交,这样的角叫圆周角。 2. 【圆周角的性质】 (3)在同圆(或等圆)中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半; 相等的圆周角所对的弧相等;
(2)一条弧所对的圆周角等于该弧所对的圆心角的一半;(1)半圆或直径所对的圆周角都相等,都等于90°(直角). 90°的圆周角所对的弦是圆的直径 驶向胜利的彼岸六.作业再见!
即90°的圆周角所对的弦是圆的直径 那么对于一般的圆周角,又有什么规律呢? 如图23.1.10, ∠ACB、 ∠ADB都是弧AB所对的圆周角. ∠AOB是弧AB所对的圆心角. 这几个角有什么关系呢?
试一试(1) 分别量一量图23.1.10中弧AB所对的两个圆周角的度数,比较一下. 再变动点C在圆周上的位置,看看圆周角的度数有没有变化. 你发现其中有什么规律吗?
(2) 分别量出图23.1.10中弧AB所对的圆周角和圆心角的度数,比较一下,你发现了什么规律?
我们可以发现: 圆周角的度数没有变化. 并且 圆周角的度数恰好为同弧所对的圆心角的度数的一半.
由上述操作可以猜想: 在一个圆中,一条弧所对的任意一个圆周角的大小都等于该弧所对的圆心角的一半.
为了验证这个猜想, 如图23.1.11所示, 可将圆对折,使折痕经过圆心O和圆周角的顶点C,这时可能出现三种情况: (1) 折痕是圆周角的一条边, (2) 折痕在圆周角的内部, (3) 折痕在圆周角的外部. 我们来分析一下第一种情况: 如图23.1.11(1), 由于OA=OC,因此 ∠A=∠C,
而∠AOB是△OAC的外角, 所以∠C=∠AOB.对(2)、(3),有同样的结论.
由此,可以得出: 【一条弧所对的圆周角等于该弧所对的圆心角的一半】. 因此我们可以知道:【在同圆(或等圆)中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半; 相等的圆周角所对的弧相等】.
三、应用举例解 例2 如图23.1.12,AB是⊙O的直径,∠A=80°.求∠ABC的度数.因为AB是⊙O的直径,而直径所对的圆周角是直角,所以 ∠ABC=180°-∠A-∠ACB
=180°-80°-90°
=10° 驶向胜利的彼岸四、课堂练习试找出图中所有相等的圆周角.2.在圆中,一条弧所对的圆心角和圆周角分别为(2x+100)°和(5x-30)°,求这条弧所对的圆心角和圆周角的度数.
练习:130°1.AB、AC为⊙O的两条弦,延长CA到D,使 AD=AB,如果∠ADB=35° ,
求∠BOC的度数。∠BOC =140° ∠A=21° 五.课堂小结1. 【圆周角的定义】 顶点在圆上,两边都与圆相交,这样的角叫圆周角。 2. 【圆周角的性质】 (3)在同圆(或等圆)中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半; 相等的圆周角所对的弧相等;
(2)一条弧所对的圆周角等于该弧所对的圆心角的一半;(1)半圆或直径所对的圆周角都相等,都等于90°(直角). 90°的圆周角所对的弦是圆的直径 驶向胜利的彼岸六.作业再见!
同课章节目录
