2022-2023年人教版(2019)新教材高中物理必修2 第5章抛体运动第2节运动的合成与分解课件(共18张PPT)
文档属性
| 名称 | 2022-2023年人教版(2019)新教材高中物理必修2 第5章抛体运动第2节运动的合成与分解课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-11-08 21:50:20 | ||
图片预览




文档简介
(共18张PPT)
5.2 运动的合成与分解
第五章 抛体运动
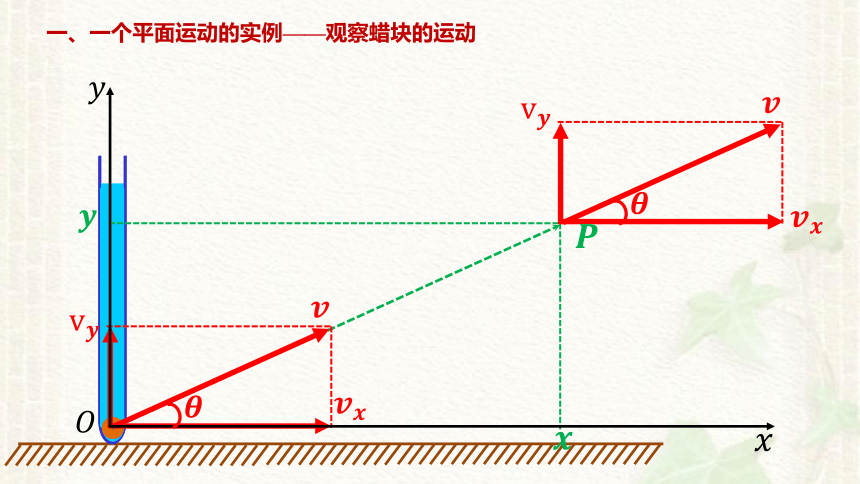
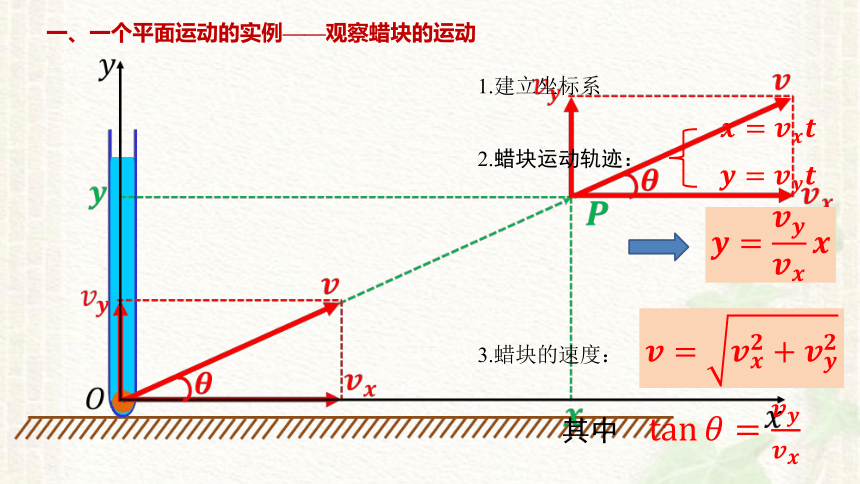
一、一个平面运动的实例——观察蜡块的运动
1.建立坐标系
2.蜡块运动轨迹:
3.蜡块的速度:
其中
一、一个平面运动的实例——观察蜡块的运动
1.合运动与分运动
(1)如果物体同时参与了几个运动,那么物体实际发生的运动就是合运动,参与的几个运动就是分运动.
(2)物体实际运动的位移、速度、加速度是它的合位移、合速度、合加速度,而分运动的位移、速度、加速度就是它的分位移、分速度、分加速度.
2.运动的合成与分解:
①由分运动求合运动的过程,叫作运动的合成;
②由合运动求分运动的过程,叫作运动的分解.
3.运动的合成与分解遵从矢量运算法则.
二、运动的合成与分解
4.合运动与分运动的四个特性
等时性 各分运动与合运动同时发生和结束,时间相同
等效性 各分运动的共同效果与合运动的效果相同
同体性 各分运动与合运动是同一物体的运动
独立性 各分运动之间互不相干,彼此独立,互不影响
二、运动的合成与分解
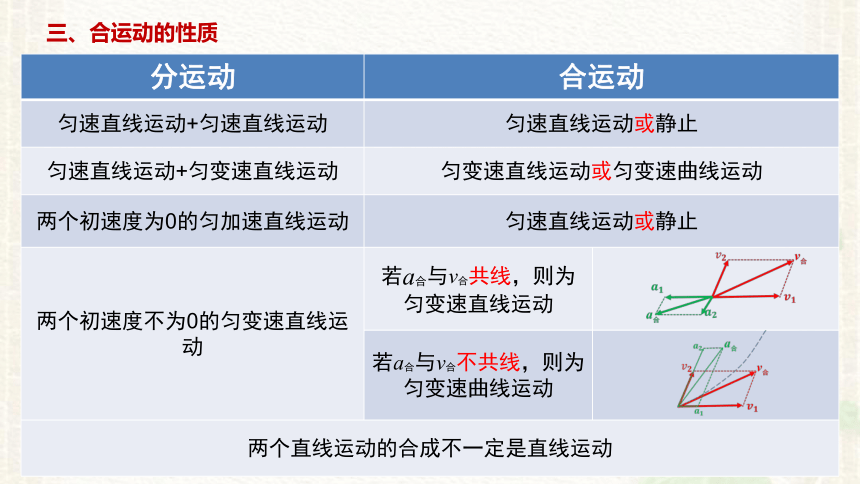
分运动 合运动
匀速直线运动+匀速直线运动 匀速直线运动或静止
匀速直线运动+匀变速直线运动 匀变速直线运动或匀变速曲线运动
两个初速度为0的匀加速直线运动 匀速直线运动或静止
两个初速度不为0的匀变速直线运动 若a合与v合共线,则为匀变速直线运动
若a合与v合不共线,则为匀变速曲线运动
两个直线运动的合成不一定是直线运动
三、合运动的性质
1.课堂上老师为了研究运动的合成与分解做了如下实验:在一端封闭、长约1m的玻璃管内注满清水,水中放一个蜡烛做的蜡块,将玻璃管的开口端用胶塞塞紧,然后将这个玻璃管倒置,在蜡块沿玻璃管上升的同时,将玻璃管水平向右移动。从某时刻开始计时,蜡块在玻璃管内每1s内上升的距离都是6cm,玻璃管向右匀加速平移,每1s内通过的水平位移依次是4cm、8cm、12cm、16cm。图乙中,y表示蜡块竖直方向的位移,x表示蜡块随玻璃管通过的水平位移,t=0时蜡块位于坐标原点:
(1)为了研究蜡块的实际运动,分别研究了蜡块在x、y方向上的运动,这运用了物理学中的______.
A.理想实验法 B 控制变量法 C.等效替代法 D.极限法
(2)根据题中数据及信息,在图乙中补上第2秒末的位置,并画出蜡块的运动轨迹___________;
(3)玻璃管向右平移的加速度a=___________m/s2.
(4)t=2s时蜡块的速度v=___________m/s.
四、随堂练习
解析:(1)类似验证力的平行四边形原则实验,本实验运用两个方向的分运动代替合运动,是等效替代法。
(2)初速度竖直向上,合外力向右,根据曲线运动轨迹特点,轨迹如图
(3)根据水平方向相等时间间隔位移差的性质,
(4)竖直方向上的分速度x=v0t+at2
将数值代入,x为第一段的位移,
即有0.04m=v0×1s+×0.04m/s2×(1s)2
解得v0=0.02 m/s
那么水平分速度vx= v0+at=0.1m/s
根据平行四边形定则得
四、随堂练习
2.雨滴由静止开始下落(不计空气阻力),遇到水平方向吹来的风,设风对雨滴持续作用,下列说法中正确的是( )
A.风速越大,雨滴下落时间将越长 B.风速越大,雨滴落地的瞬时速度越大
C.雨滴着地时的速度与风速无关 D.雨滴下落的时间与风速无关
解析:分运动和合运动具有等时性,在竖直方向上,仅受重力,做自由落体运动,高度不变,所以运动时间不变,即雨滴下落的时间与风速无关,故A错误,D正确;
雨滴落地时竖直方向的速度不变,风力越大,水平方向上的加速度越大,时间不变,则落地时水平方向上速度越大,根据平行四边形定则,落地的速度越大,故B正确,C错误。
故选BD
点睛:解决本题的关键将雨滴的运动分解为水平方向和竖直方向,知道两方向上的运动情况以及知道分运动和合运动具有等时性。
四、随堂练习
3.关于运动的合成,下列说法中正确的是:( )
A.两个分运动的时间一定与它们的合运动的时间相等
B.合运动的时间等于两个分运动的时间之和
C.合运动的速度一定比每一个分运动的速度大
D.只要两个分运动是直线运动,那么合运动也一定是直线运动
解析:分运动与合运动具有等时性,故A正确,B错误;
根据平行四边形定则,知合速度可能比分速度大,可能比分速度小,可能与分速度相等,故C错误;
两个分运动是直线运动,那么合运动也不一定是直线运动,比如:平抛运动,而两个匀速直线运动的合运动一定是匀速直线运动,故 D错误。
故选A。
四、随堂练习
4.有两个不共线的直线运动,初速度分别为v1和v2,加速度恒定,分别为a1和a2,关于合运动,下列说法正确的是( )
A.若v1=0,v2≠0,a1≠0,a2≠0,则合运动一定是匀变速曲线运动
B.若v1=0,v2=0,a1≠0,a2≠0,则合运动一定是匀变速直线运动
C.若v1≠0,v2≠0,a1=0,a2=0,则合运动一定是匀速直线运动
D.若v1≠0,v2≠0,a1≠0,a2≠0,则合运动一定是匀变速曲线运动
解析:
A.若v1=0,v2≠0,a1≠0,a2≠0,即合初速度与合加速度不在同一直线上,则合运动一定是匀变速曲线运动,故A正确;
B.若v1=0,v2=0,a1≠0,a2≠0,即合初速度为零,则合运动一定是沿与合加速度方向共线的匀变速直线运动,故B正确;
C.若v1≠0,v2≠0,a1=0,a2=0,即合加速度为零,则合运动一定是匀速直线运动,故C正确;
D.若v1≠0,v2≠0,a1≠0,a2≠0,当合初速度与合加速度在同一直线上时,合运动是匀变速直线运动,故D错误。故选ABC。
四、随堂练习
5.一质点在xOy平面内的运动轨迹如图所示,下列判断正确的是( )
A.质点沿x轴方向可能做匀速运动
B.质点沿y轴方向不可能做变速运动
C.若质点沿y轴方向始终匀速运动,则沿x轴方向可能先加速后减速
D.若质点沿y轴方向始终匀速运动,则沿x轴方向可能先减速后加速
解析:质点做曲线运动,合力指向曲线内侧,即加速度方向指向曲线内侧,不能只沿y轴方向,所以在x轴方向一定有分量,所以沿x轴不可能做匀速运动,y轴方向可能有加速度分量,y轴方向可能做变速运动,故AB错误;
质点在y轴做匀速直线,则加速度沿x轴方向,质点沿x轴先沿正方向运动再沿负方向运动,最终x轴方向位移为0,所以物体沿x轴方向不可能先加速后减速,可能先减速后加速,故C错误,D正确。
故选D。
四、随堂练习
6.物体在直角坐标系xOy所在平面内由O点开始运动,其沿坐标轴方向的两个分速度随时间变化的图像如图7所示,则对该物体运动过程的描述正确的是( )
A.物体在0~3 s做匀变速直线运动
B.物体在0~3 s做匀变速曲线运动
C.物体在3~4 s做变加速直线运动
D.物体在3~4 s做匀变速曲线运动
四、随堂练习
解析:物体在0~3 s内,由题意可知,
x方向做vx=4 m/s的匀速直线运动,
y方向做初速度为0、加速度ay=1 m/s2的匀加速直线运动,
合初速度v0=vx=4 m/s,合加速度a=ay=1 m/s2,
物体的合初速度与合加速度不在同一直线上,
所以物体的合运动为匀变速曲线运动,如图甲所示,A错误,B正确.
物体在3~4 s内,
x方向做初速度vx=4 m/s、加速度ax=-4 m/s2的匀减速直线运动,
y方向做初速度vy=3 m/s、加速度ay=-3 m/s2的匀减速直线运动,
合初速度大小v=5 m/s,合加速度大小a=5 m/s2,v、a方向恰好相反,
所以物体的合运动为匀减速直线运动,如图乙所示,C、D错误.
四、随堂练习
7.如图所示,玻璃生产线上,宽为d的成型玻璃以v1速度连续不断地在平直的轨道上前进,在切割工序处,金刚石切割刀以相对的速度v2切割玻璃,且每次割下的玻璃板都成规定尺寸的矩形,以下说法正确的是( )
A.切割一次的时间为
B.切割刀切割一次所走的距离为
C.速度v2的方向应由O指向c,且cosθ=
D.速度v2的方向应由O指向a,且v1与v2的合速度方向沿Ob
解析:因玻璃板以速度v1匀速前进,而刀具对其相对速度必须为垂直于v1方向才能割成矩形,故刀具对地速度方向方向沿Oc才有可能,且此时刀具有平行于v1方向上有v1大小的分速度,则v2cosθ=v1,切割一次用时.故选C.
四、随堂练习
8.在杂技表演中,猴子沿竖直杆向上做初速度为0、加速度为a的匀加速运动,同时人顶着直杆以速度v0水平匀速前进,经过时间t,猴子沿杆向上移动的高度为h,人顶杆沿水平地面移动的距离为x,如图所示.关于猴子的运动情况,下列说法中正确的是( )
A.相对地面的运动轨迹为直线
B.相对地面做匀变速曲线运动
C.T时刻猴子相对地面的速度大小为v0+at
D.t时间内猴子相对地面的位移大小为2
解析:A.猴子在水平方向上做匀速直线运动,竖直方向上做初速度为0的匀加速直线运动,猴子相对地面的运动轨迹为曲线,A错误;
B.因为猴子受到的合外力恒定(加速度恒定),所以相对地面猴子做的是匀变速曲线运动,B正确;
C.t时刻猴子对地的水平速度为v0,竖直速度为at,因此合速度大小为v=,C错误
D.t时间内猴子对地的位移大小为s=,D错误。故选B。
四、随堂练习
9.如图所示,一块橡皮用细线悬挂于O点,用钉子靠着线的左侧,沿与水平方向成30°角的斜面向右以速度v匀速运动,运动中始终保持悬线竖直,下列说法正确的是( )
A.橡皮的速度大小为
B.橡皮的速度大小为
C.橡皮的速度与水平方向成30°角
D.橡皮的速度与水平方向成60°角
解析:橡皮参与了平行于斜面方向的匀速直线运动和竖直方向上的匀速直线运动,两个分速度大小相等,都为v,根据平行四边形定则知:,合速度的方向与水平方向的夹角为,故BD正确,AC错误.
点睛:橡皮参与了平行于斜面方向的匀速直线运动和竖直方向上的匀速直线运动,根据平行四边形定则确定合速度的大小和方向.
四、随堂练习
10.如图所示,细线一端固定在天花板上的O点,另一端穿过一张CD光盘的中央圆孔后拴着一个橡胶球。橡胶球静止时,竖直悬线刚好挨着水平桌面的边沿。现将CD光盘按在桌面上,并沿桌面边缘以速度v匀速移动,移动过程中,CD光盘中央小孔始终紧挨桌面边线。当悬线与竖直方向的夹角为45°时( )
A.小球的竖直分速度大小为v
B.小球的竖直分速度大小为v
C.小球的速度大小为v
D.小球的速度大小为v
解析:小球始终在光盘的正下方,所以小球水平方向的速度为
小球距离桌面越来越近,所以在竖直方向的速度等于CD盘下方绳子变短的速度。当悬线与竖直方向的夹角为45°时,绳子变短的速度为所以小球的速度大小为
故选BD。
四、随堂练习
5.2 运动的合成与分解
第五章 抛体运动
一、一个平面运动的实例——观察蜡块的运动
1.建立坐标系
2.蜡块运动轨迹:
3.蜡块的速度:
其中
一、一个平面运动的实例——观察蜡块的运动
1.合运动与分运动
(1)如果物体同时参与了几个运动,那么物体实际发生的运动就是合运动,参与的几个运动就是分运动.
(2)物体实际运动的位移、速度、加速度是它的合位移、合速度、合加速度,而分运动的位移、速度、加速度就是它的分位移、分速度、分加速度.
2.运动的合成与分解:
①由分运动求合运动的过程,叫作运动的合成;
②由合运动求分运动的过程,叫作运动的分解.
3.运动的合成与分解遵从矢量运算法则.
二、运动的合成与分解
4.合运动与分运动的四个特性
等时性 各分运动与合运动同时发生和结束,时间相同
等效性 各分运动的共同效果与合运动的效果相同
同体性 各分运动与合运动是同一物体的运动
独立性 各分运动之间互不相干,彼此独立,互不影响
二、运动的合成与分解
分运动 合运动
匀速直线运动+匀速直线运动 匀速直线运动或静止
匀速直线运动+匀变速直线运动 匀变速直线运动或匀变速曲线运动
两个初速度为0的匀加速直线运动 匀速直线运动或静止
两个初速度不为0的匀变速直线运动 若a合与v合共线,则为匀变速直线运动
若a合与v合不共线,则为匀变速曲线运动
两个直线运动的合成不一定是直线运动
三、合运动的性质
1.课堂上老师为了研究运动的合成与分解做了如下实验:在一端封闭、长约1m的玻璃管内注满清水,水中放一个蜡烛做的蜡块,将玻璃管的开口端用胶塞塞紧,然后将这个玻璃管倒置,在蜡块沿玻璃管上升的同时,将玻璃管水平向右移动。从某时刻开始计时,蜡块在玻璃管内每1s内上升的距离都是6cm,玻璃管向右匀加速平移,每1s内通过的水平位移依次是4cm、8cm、12cm、16cm。图乙中,y表示蜡块竖直方向的位移,x表示蜡块随玻璃管通过的水平位移,t=0时蜡块位于坐标原点:
(1)为了研究蜡块的实际运动,分别研究了蜡块在x、y方向上的运动,这运用了物理学中的______.
A.理想实验法 B 控制变量法 C.等效替代法 D.极限法
(2)根据题中数据及信息,在图乙中补上第2秒末的位置,并画出蜡块的运动轨迹___________;
(3)玻璃管向右平移的加速度a=___________m/s2.
(4)t=2s时蜡块的速度v=___________m/s.
四、随堂练习
解析:(1)类似验证力的平行四边形原则实验,本实验运用两个方向的分运动代替合运动,是等效替代法。
(2)初速度竖直向上,合外力向右,根据曲线运动轨迹特点,轨迹如图
(3)根据水平方向相等时间间隔位移差的性质,
(4)竖直方向上的分速度x=v0t+at2
将数值代入,x为第一段的位移,
即有0.04m=v0×1s+×0.04m/s2×(1s)2
解得v0=0.02 m/s
那么水平分速度vx= v0+at=0.1m/s
根据平行四边形定则得
四、随堂练习
2.雨滴由静止开始下落(不计空气阻力),遇到水平方向吹来的风,设风对雨滴持续作用,下列说法中正确的是( )
A.风速越大,雨滴下落时间将越长 B.风速越大,雨滴落地的瞬时速度越大
C.雨滴着地时的速度与风速无关 D.雨滴下落的时间与风速无关
解析:分运动和合运动具有等时性,在竖直方向上,仅受重力,做自由落体运动,高度不变,所以运动时间不变,即雨滴下落的时间与风速无关,故A错误,D正确;
雨滴落地时竖直方向的速度不变,风力越大,水平方向上的加速度越大,时间不变,则落地时水平方向上速度越大,根据平行四边形定则,落地的速度越大,故B正确,C错误。
故选BD
点睛:解决本题的关键将雨滴的运动分解为水平方向和竖直方向,知道两方向上的运动情况以及知道分运动和合运动具有等时性。
四、随堂练习
3.关于运动的合成,下列说法中正确的是:( )
A.两个分运动的时间一定与它们的合运动的时间相等
B.合运动的时间等于两个分运动的时间之和
C.合运动的速度一定比每一个分运动的速度大
D.只要两个分运动是直线运动,那么合运动也一定是直线运动
解析:分运动与合运动具有等时性,故A正确,B错误;
根据平行四边形定则,知合速度可能比分速度大,可能比分速度小,可能与分速度相等,故C错误;
两个分运动是直线运动,那么合运动也不一定是直线运动,比如:平抛运动,而两个匀速直线运动的合运动一定是匀速直线运动,故 D错误。
故选A。
四、随堂练习
4.有两个不共线的直线运动,初速度分别为v1和v2,加速度恒定,分别为a1和a2,关于合运动,下列说法正确的是( )
A.若v1=0,v2≠0,a1≠0,a2≠0,则合运动一定是匀变速曲线运动
B.若v1=0,v2=0,a1≠0,a2≠0,则合运动一定是匀变速直线运动
C.若v1≠0,v2≠0,a1=0,a2=0,则合运动一定是匀速直线运动
D.若v1≠0,v2≠0,a1≠0,a2≠0,则合运动一定是匀变速曲线运动
解析:
A.若v1=0,v2≠0,a1≠0,a2≠0,即合初速度与合加速度不在同一直线上,则合运动一定是匀变速曲线运动,故A正确;
B.若v1=0,v2=0,a1≠0,a2≠0,即合初速度为零,则合运动一定是沿与合加速度方向共线的匀变速直线运动,故B正确;
C.若v1≠0,v2≠0,a1=0,a2=0,即合加速度为零,则合运动一定是匀速直线运动,故C正确;
D.若v1≠0,v2≠0,a1≠0,a2≠0,当合初速度与合加速度在同一直线上时,合运动是匀变速直线运动,故D错误。故选ABC。
四、随堂练习
5.一质点在xOy平面内的运动轨迹如图所示,下列判断正确的是( )
A.质点沿x轴方向可能做匀速运动
B.质点沿y轴方向不可能做变速运动
C.若质点沿y轴方向始终匀速运动,则沿x轴方向可能先加速后减速
D.若质点沿y轴方向始终匀速运动,则沿x轴方向可能先减速后加速
解析:质点做曲线运动,合力指向曲线内侧,即加速度方向指向曲线内侧,不能只沿y轴方向,所以在x轴方向一定有分量,所以沿x轴不可能做匀速运动,y轴方向可能有加速度分量,y轴方向可能做变速运动,故AB错误;
质点在y轴做匀速直线,则加速度沿x轴方向,质点沿x轴先沿正方向运动再沿负方向运动,最终x轴方向位移为0,所以物体沿x轴方向不可能先加速后减速,可能先减速后加速,故C错误,D正确。
故选D。
四、随堂练习
6.物体在直角坐标系xOy所在平面内由O点开始运动,其沿坐标轴方向的两个分速度随时间变化的图像如图7所示,则对该物体运动过程的描述正确的是( )
A.物体在0~3 s做匀变速直线运动
B.物体在0~3 s做匀变速曲线运动
C.物体在3~4 s做变加速直线运动
D.物体在3~4 s做匀变速曲线运动
四、随堂练习
解析:物体在0~3 s内,由题意可知,
x方向做vx=4 m/s的匀速直线运动,
y方向做初速度为0、加速度ay=1 m/s2的匀加速直线运动,
合初速度v0=vx=4 m/s,合加速度a=ay=1 m/s2,
物体的合初速度与合加速度不在同一直线上,
所以物体的合运动为匀变速曲线运动,如图甲所示,A错误,B正确.
物体在3~4 s内,
x方向做初速度vx=4 m/s、加速度ax=-4 m/s2的匀减速直线运动,
y方向做初速度vy=3 m/s、加速度ay=-3 m/s2的匀减速直线运动,
合初速度大小v=5 m/s,合加速度大小a=5 m/s2,v、a方向恰好相反,
所以物体的合运动为匀减速直线运动,如图乙所示,C、D错误.
四、随堂练习
7.如图所示,玻璃生产线上,宽为d的成型玻璃以v1速度连续不断地在平直的轨道上前进,在切割工序处,金刚石切割刀以相对的速度v2切割玻璃,且每次割下的玻璃板都成规定尺寸的矩形,以下说法正确的是( )
A.切割一次的时间为
B.切割刀切割一次所走的距离为
C.速度v2的方向应由O指向c,且cosθ=
D.速度v2的方向应由O指向a,且v1与v2的合速度方向沿Ob
解析:因玻璃板以速度v1匀速前进,而刀具对其相对速度必须为垂直于v1方向才能割成矩形,故刀具对地速度方向方向沿Oc才有可能,且此时刀具有平行于v1方向上有v1大小的分速度,则v2cosθ=v1,切割一次用时.故选C.
四、随堂练习
8.在杂技表演中,猴子沿竖直杆向上做初速度为0、加速度为a的匀加速运动,同时人顶着直杆以速度v0水平匀速前进,经过时间t,猴子沿杆向上移动的高度为h,人顶杆沿水平地面移动的距离为x,如图所示.关于猴子的运动情况,下列说法中正确的是( )
A.相对地面的运动轨迹为直线
B.相对地面做匀变速曲线运动
C.T时刻猴子相对地面的速度大小为v0+at
D.t时间内猴子相对地面的位移大小为2
解析:A.猴子在水平方向上做匀速直线运动,竖直方向上做初速度为0的匀加速直线运动,猴子相对地面的运动轨迹为曲线,A错误;
B.因为猴子受到的合外力恒定(加速度恒定),所以相对地面猴子做的是匀变速曲线运动,B正确;
C.t时刻猴子对地的水平速度为v0,竖直速度为at,因此合速度大小为v=,C错误
D.t时间内猴子对地的位移大小为s=,D错误。故选B。
四、随堂练习
9.如图所示,一块橡皮用细线悬挂于O点,用钉子靠着线的左侧,沿与水平方向成30°角的斜面向右以速度v匀速运动,运动中始终保持悬线竖直,下列说法正确的是( )
A.橡皮的速度大小为
B.橡皮的速度大小为
C.橡皮的速度与水平方向成30°角
D.橡皮的速度与水平方向成60°角
解析:橡皮参与了平行于斜面方向的匀速直线运动和竖直方向上的匀速直线运动,两个分速度大小相等,都为v,根据平行四边形定则知:,合速度的方向与水平方向的夹角为,故BD正确,AC错误.
点睛:橡皮参与了平行于斜面方向的匀速直线运动和竖直方向上的匀速直线运动,根据平行四边形定则确定合速度的大小和方向.
四、随堂练习
10.如图所示,细线一端固定在天花板上的O点,另一端穿过一张CD光盘的中央圆孔后拴着一个橡胶球。橡胶球静止时,竖直悬线刚好挨着水平桌面的边沿。现将CD光盘按在桌面上,并沿桌面边缘以速度v匀速移动,移动过程中,CD光盘中央小孔始终紧挨桌面边线。当悬线与竖直方向的夹角为45°时( )
A.小球的竖直分速度大小为v
B.小球的竖直分速度大小为v
C.小球的速度大小为v
D.小球的速度大小为v
解析:小球始终在光盘的正下方,所以小球水平方向的速度为
小球距离桌面越来越近,所以在竖直方向的速度等于CD盘下方绳子变短的速度。当悬线与竖直方向的夹角为45°时,绳子变短的速度为所以小球的速度大小为
故选BD。
四、随堂练习
