沪科版九年级上册22.4 图形的位似变换 课件(共34张PPT)
文档属性
| 名称 | 沪科版九年级上册22.4 图形的位似变换 课件(共34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-09 07:55:05 | ||
图片预览











文档简介
(共34张PPT)
22.4 图形的位似变换
第二十二章 相似形
逐点
学练
本节小结
作业提升
学习目标
本节要点
1
学习流程
2
位似图形的定义
位似图形的性质
位似图形的画法
平面直角坐标系中图形的位似变换
知识点
位似图形的定义
感悟新知
1
1. 位似图形与位似变换
一般地,如果一个图形上的点 A1, B1,…, P1 和另一个图形上的点 A, B,…, P 分别对应,并且满足下面两点:
(1)直线 AA1, BB1,…, PP1 都经过同一点 O;
(2) = =…=OP1OP =k.
感悟新知
那么,这两个图形叫做位似图形,点 O 叫做位似中心 . 这两个图形之间的变换叫做位似变换 .
注意: 两个位似图形的位似中心有且只有一个 .
感悟新知
2. 位似与相似的关系
(1)相似仅要求两个图形形状完全相同,而位似是在相似的基础上要求对应顶点的连线相交于一点;
(2)如果两个图形是位似图形,那么这两个图形必是相似图形,但是相似的两个图形不一定是位似图形,因此 , 位似是相似的特殊情况 .
感悟新知
特别提醒:
位似中心可能位于两个位似图形的同侧, 也可能位 于两个位似图形之间, 还可能位于两个位似图形的内部 或边上或 某一个顶点处 . 常见位似图形 的构成如图 22.4-1所示 .
感悟新知
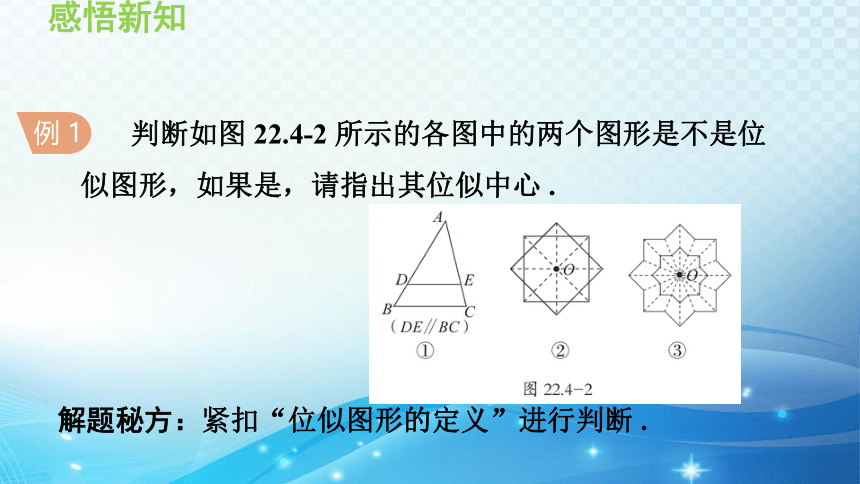
例 1
判断如图 22.4-2 所示的各图中的两个图形是不是位
似图形,如果是,请指出其位似中心 .
解题秘方:紧扣“位似图形的定义”进行判断 .
感悟新知
方法提醒
判断两个图形是否为位似图形的方法:
首先看这两个图形是否相似;
然后看每组对应顶点的连线是否交于一点.
感悟新知
解: ①是位似图形,位似中心为点 A;
②不是位似图形;
③是位似图形,位似中心为点 O.
感悟新知
知识点
位似图形的性质
2
位似图形具有的性质
(1)位似图形每组对应顶点的连线必过位似中心;
(2)位似图形任意一组对应点到位似中心的距离之比等于相似比;
(3)位似图形的对应线段平行(或在一条直线上),且对应线段之比相等;
感悟新知
(4)两个图形位似,则两个图形必相似,其周长比等于相似比,面积比等于相似比的平方 .
感悟新知
特别提醒:
1. 位似图形是相似图形,所以它具有相似图形的一切特征 .
2. 位似与平移、轴对称、旋转一样,是图形的变换方式,但位似可以改变图形的位置和大小,即位似是图形的相似变换 .
感悟新知
例2
找出如图 22.4-3 所示的位似图形的位似中心 .
感悟新知
解题秘方:紧扣“位似图形每组对应顶点的连线必过位似中心”进行查找 .
方法提醒
确定位似图形的位似中心时,要认真观察图形,寻找对应顶点,然后经过每组对应顶点作直线,它们的交点即为位似中心 .
注意:实际作图时,只需作出两组对应顶点的连线即可 .
感悟新知
解:如图 22.4-4,点 P1, P2, P3 即为所求的位似中心 .
感悟新知
知识点
位似图形的画法
3
画位似图形的步骤
(1)确定位似中心(位似中心可以在图形外部,也可以在图形内部,还可以在图形的边上或某一个顶点处) ;
(2)分别连接位似中心和能代表原图的关键点,并延长;
(3)根据相似比,确定所画位似图形的关键点的位置;
感悟新知
(4)顺次连接所作各点,得到放大或缩小的图形 .
注意: 画位似图形时,要弄清相似比,即分清是已知图形与新图形的相似比,还是新图形与已知图形的相似比 .
感悟新知
例 3
[ 开放题 ] 如图 22.4-5,已知四边形 ABCD,将四边形 ABCD 放大,使放大后的图形与原图形是位似图形,且放大后的图形与原图形对应线段的比为 2 ∶ 1.
解题秘方:紧扣“位似图形的定义和性质”,按画位似图形的步骤作图 .
感悟新知
解: 根据位似中心的不同位置情况进行作图(画法不唯一) .
画法一 位似中心在四边形的顶点上,如图 22.4-6,以点 A 为位似中心,四边形 AB1C1D1 就是所求作的图形 .
画法二 位似中心在四边形的边上,如图 22.4-7,以 AD边上一点为位似中心,四边形 A1B1C1D1 就是所求作的图形 .
感悟新知
另解
位似中心在四边形内部,如图 22.4-8,以四边形 ABCD 内部一点为 位 似 中 心, 四 边 形A1B1C1D1 就 是 所 求 作 的图形 .
位似中心在四边形外部,如图 22.4-9,以四边形 ABCD 外部一点为 位 似 中 心, 四 边 形A1B1C1D1 就 是 所 求 作 的图形 .
感悟新知
知识点
平面直角坐标系中图形的位似变换
4
1. 位似变换时对应点的坐标变化规律
在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为 k,那么位似图形对应点的坐标的比等于 k或 -k.
注意: 这里的相似比指的是新图形与原图形的对应边的比 .
感悟新知
2. 位似变换与平移、轴对称、旋转三种变换的联系和区别
(1)位似、平移、轴对称、旋转都是图形变换的基本形式,它们的本质区别在于:平移、轴对称、旋转三种图形变换是全等变换,而位似变换是相似变换 .
(2)在直角坐标系中,把一个图形进行平移、轴对称、旋转或位似变换,其对应点的坐标都有各自的变化规律:
感悟新知
① 平移变换是横坐标或纵坐标加上(或减去)平移的距离;
②在轴对称变换中,以 x 轴为对称轴,则对应点的横坐标相等,纵坐标互为相反数;以 y 轴为对称轴,则纵坐标相等,横坐标互为相反数;
③在旋转变换中,一个图形绕原点旋转 180°,则旋转前后两个图形对应点的横坐标与纵坐标都分别互为相反数;
感悟新知
④在位似变换中,当以原点为位似中心时,变换后与变换前两个图形对应点的横坐标之比的绝对值、纵坐标之比的绝对值都等于变换后的图形与变换前的图形的相似比 .
感悟新知
特别提醒
在平面直角坐标系中,以原点为位似中心时,使位似图形与原图形的相似比为k,那么:
当位似图形与原图形在原点的同侧时,原图形上的点(x,y)对应的位似图形上的点的坐标为(kx,ky);
感悟新知
当位似图形与原图形在原点的两侧时,原图形上的点(x,y)对应的位似图形上的点的坐标为(-kx,-ky).
当 k>1 时,图形扩大为原来的 k 倍;
当 0感悟新知
例4
[ 模拟·山东) 在如图 22.4-10 的方格纸中,△ OAB的 顶 点 坐 标 分 别 为 O(0,0), A(-2, -1), B(- 1,-3),△ O1A1B1 是△ OAB 以点 P 为位似中心的位似图形.
感悟新知
解题秘方:根据位似中心是对应点所在直线的交点确定位似中心的坐标,再利用位似变换时对应点的坐标变化规律求对应点的坐标 .
感悟新知
解:位似中心 P 的位置如图 22.4-11 所示,
P(-5,-1), B1(3, -5);
(1)在图中标出位似中心 P 的位置,并写出点 P 及点 B
的对应点 B1 的坐标;
感悟新知
解:△ OA2B2 如图 22.4-11 所示, B2( -2, -6);
(2)以原点O为位似中心, 在位似中心的同侧画出△ OAB 的一个位似 △ OA2B2, 使它与△ OAB 的相似比为2 ∶ 1,并写出点 B 的对应点 B2 的坐标;
感悟新知
解:点 M2(2a,2b).
(3) △ OAB 的内部一点 M 的坐标为(a, b),写出 M在△ OA2B2 中的对应点 M2 的坐标.
感悟新知
特别提醒
以原点为位似中心的位似图形的坐标变化一定要注意坐标符号的变化,简单地说,若两个图形在原点同侧,则坐标符号不变;若两个图形在原点异侧,则坐标符号相反 .
本节小结
图形的位似变换
位似
图形
坐标规律
画法
定义
性质
请完成教材课后习题
作业提升
22.4 图形的位似变换
第二十二章 相似形
逐点
学练
本节小结
作业提升
学习目标
本节要点
1
学习流程
2
位似图形的定义
位似图形的性质
位似图形的画法
平面直角坐标系中图形的位似变换
知识点
位似图形的定义
感悟新知
1
1. 位似图形与位似变换
一般地,如果一个图形上的点 A1, B1,…, P1 和另一个图形上的点 A, B,…, P 分别对应,并且满足下面两点:
(1)直线 AA1, BB1,…, PP1 都经过同一点 O;
(2) = =…=OP1OP =k.
感悟新知
那么,这两个图形叫做位似图形,点 O 叫做位似中心 . 这两个图形之间的变换叫做位似变换 .
注意: 两个位似图形的位似中心有且只有一个 .
感悟新知
2. 位似与相似的关系
(1)相似仅要求两个图形形状完全相同,而位似是在相似的基础上要求对应顶点的连线相交于一点;
(2)如果两个图形是位似图形,那么这两个图形必是相似图形,但是相似的两个图形不一定是位似图形,因此 , 位似是相似的特殊情况 .
感悟新知
特别提醒:
位似中心可能位于两个位似图形的同侧, 也可能位 于两个位似图形之间, 还可能位于两个位似图形的内部 或边上或 某一个顶点处 . 常见位似图形 的构成如图 22.4-1所示 .
感悟新知
例 1
判断如图 22.4-2 所示的各图中的两个图形是不是位
似图形,如果是,请指出其位似中心 .
解题秘方:紧扣“位似图形的定义”进行判断 .
感悟新知
方法提醒
判断两个图形是否为位似图形的方法:
首先看这两个图形是否相似;
然后看每组对应顶点的连线是否交于一点.
感悟新知
解: ①是位似图形,位似中心为点 A;
②不是位似图形;
③是位似图形,位似中心为点 O.
感悟新知
知识点
位似图形的性质
2
位似图形具有的性质
(1)位似图形每组对应顶点的连线必过位似中心;
(2)位似图形任意一组对应点到位似中心的距离之比等于相似比;
(3)位似图形的对应线段平行(或在一条直线上),且对应线段之比相等;
感悟新知
(4)两个图形位似,则两个图形必相似,其周长比等于相似比,面积比等于相似比的平方 .
感悟新知
特别提醒:
1. 位似图形是相似图形,所以它具有相似图形的一切特征 .
2. 位似与平移、轴对称、旋转一样,是图形的变换方式,但位似可以改变图形的位置和大小,即位似是图形的相似变换 .
感悟新知
例2
找出如图 22.4-3 所示的位似图形的位似中心 .
感悟新知
解题秘方:紧扣“位似图形每组对应顶点的连线必过位似中心”进行查找 .
方法提醒
确定位似图形的位似中心时,要认真观察图形,寻找对应顶点,然后经过每组对应顶点作直线,它们的交点即为位似中心 .
注意:实际作图时,只需作出两组对应顶点的连线即可 .
感悟新知
解:如图 22.4-4,点 P1, P2, P3 即为所求的位似中心 .
感悟新知
知识点
位似图形的画法
3
画位似图形的步骤
(1)确定位似中心(位似中心可以在图形外部,也可以在图形内部,还可以在图形的边上或某一个顶点处) ;
(2)分别连接位似中心和能代表原图的关键点,并延长;
(3)根据相似比,确定所画位似图形的关键点的位置;
感悟新知
(4)顺次连接所作各点,得到放大或缩小的图形 .
注意: 画位似图形时,要弄清相似比,即分清是已知图形与新图形的相似比,还是新图形与已知图形的相似比 .
感悟新知
例 3
[ 开放题 ] 如图 22.4-5,已知四边形 ABCD,将四边形 ABCD 放大,使放大后的图形与原图形是位似图形,且放大后的图形与原图形对应线段的比为 2 ∶ 1.
解题秘方:紧扣“位似图形的定义和性质”,按画位似图形的步骤作图 .
感悟新知
解: 根据位似中心的不同位置情况进行作图(画法不唯一) .
画法一 位似中心在四边形的顶点上,如图 22.4-6,以点 A 为位似中心,四边形 AB1C1D1 就是所求作的图形 .
画法二 位似中心在四边形的边上,如图 22.4-7,以 AD边上一点为位似中心,四边形 A1B1C1D1 就是所求作的图形 .
感悟新知
另解
位似中心在四边形内部,如图 22.4-8,以四边形 ABCD 内部一点为 位 似 中 心, 四 边 形A1B1C1D1 就 是 所 求 作 的图形 .
位似中心在四边形外部,如图 22.4-9,以四边形 ABCD 外部一点为 位 似 中 心, 四 边 形A1B1C1D1 就 是 所 求 作 的图形 .
感悟新知
知识点
平面直角坐标系中图形的位似变换
4
1. 位似变换时对应点的坐标变化规律
在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为 k,那么位似图形对应点的坐标的比等于 k或 -k.
注意: 这里的相似比指的是新图形与原图形的对应边的比 .
感悟新知
2. 位似变换与平移、轴对称、旋转三种变换的联系和区别
(1)位似、平移、轴对称、旋转都是图形变换的基本形式,它们的本质区别在于:平移、轴对称、旋转三种图形变换是全等变换,而位似变换是相似变换 .
(2)在直角坐标系中,把一个图形进行平移、轴对称、旋转或位似变换,其对应点的坐标都有各自的变化规律:
感悟新知
① 平移变换是横坐标或纵坐标加上(或减去)平移的距离;
②在轴对称变换中,以 x 轴为对称轴,则对应点的横坐标相等,纵坐标互为相反数;以 y 轴为对称轴,则纵坐标相等,横坐标互为相反数;
③在旋转变换中,一个图形绕原点旋转 180°,则旋转前后两个图形对应点的横坐标与纵坐标都分别互为相反数;
感悟新知
④在位似变换中,当以原点为位似中心时,变换后与变换前两个图形对应点的横坐标之比的绝对值、纵坐标之比的绝对值都等于变换后的图形与变换前的图形的相似比 .
感悟新知
特别提醒
在平面直角坐标系中,以原点为位似中心时,使位似图形与原图形的相似比为k,那么:
当位似图形与原图形在原点的同侧时,原图形上的点(x,y)对应的位似图形上的点的坐标为(kx,ky);
感悟新知
当位似图形与原图形在原点的两侧时,原图形上的点(x,y)对应的位似图形上的点的坐标为(-kx,-ky).
当 k>1 时,图形扩大为原来的 k 倍;
当 0
例4
[ 模拟·山东) 在如图 22.4-10 的方格纸中,△ OAB的 顶 点 坐 标 分 别 为 O(0,0), A(-2, -1), B(- 1,-3),△ O1A1B1 是△ OAB 以点 P 为位似中心的位似图形.
感悟新知
解题秘方:根据位似中心是对应点所在直线的交点确定位似中心的坐标,再利用位似变换时对应点的坐标变化规律求对应点的坐标 .
感悟新知
解:位似中心 P 的位置如图 22.4-11 所示,
P(-5,-1), B1(3, -5);
(1)在图中标出位似中心 P 的位置,并写出点 P 及点 B
的对应点 B1 的坐标;
感悟新知
解:△ OA2B2 如图 22.4-11 所示, B2( -2, -6);
(2)以原点O为位似中心, 在位似中心的同侧画出△ OAB 的一个位似 △ OA2B2, 使它与△ OAB 的相似比为2 ∶ 1,并写出点 B 的对应点 B2 的坐标;
感悟新知
解:点 M2(2a,2b).
(3) △ OAB 的内部一点 M 的坐标为(a, b),写出 M在△ OA2B2 中的对应点 M2 的坐标.
感悟新知
特别提醒
以原点为位似中心的位似图形的坐标变化一定要注意坐标符号的变化,简单地说,若两个图形在原点同侧,则坐标符号不变;若两个图形在原点异侧,则坐标符号相反 .
本节小结
图形的位似变换
位似
图形
坐标规律
画法
定义
性质
请完成教材课后习题
作业提升
