2006年中考数学试题分类汇编及解析----圆[下学期]
文档属性
| 名称 | 2006年中考数学试题分类汇编及解析----圆[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 143.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-10 14:42:00 | ||
图片预览


文档简介
1、(2006浙江嘉兴)如图,已知△ABC,,.O是AB的中点,⊙O与AC相切于点D、与BC相切于点E.设⊙O 交OB于F,连DF并延长交CB的延长线于G.
(1)与是否相等?为什么?
(2)求由DG、GE和弧ED所围成图形的面积(阴影部分).
[解析] (1) (…1分)
连OD,∵(⊙O的半径),∴ (…2分)
∵⊙O与AC相切于点D,∴
又∵,即,∴,
∴
又∵,∴
(2)连OE,则ODCE为正方形且边长为3
∵
∴
从而
∴阴影部分的面积
=△DCG的面积-(正方形ODCE的面积-扇形ODE的面积) =
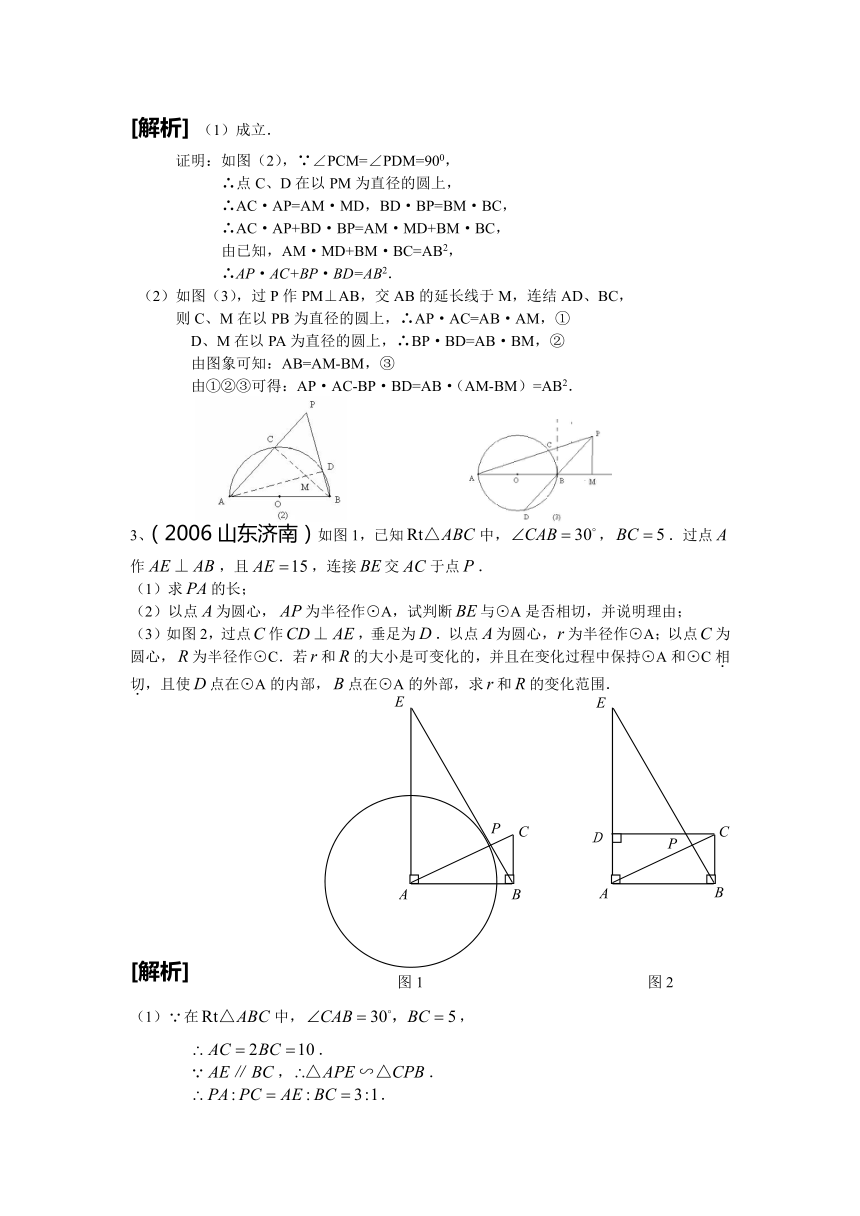
2、(2006山东日照)阅读下面的材料:
如图(1),在以AB为直径的半圆O内有一点P,AP、BP的延长线分别交半圆O于点C、D.求证:AP·AC+BP·BD=AB2.
证明:连结AD、BC,过P作PM⊥AB,则∠ADB=∠AMP=90o,
∴点D、M在以AP为直径的圆上;同理:M、C在以BP为直径的圆上.
由割线定理得: AP·AC=AM·AB,BP·BD=BM·BA,
所以,AP·AC+BP·BD=AM·AB+BM·AB=AB·(AM+BM)=AB2.
当点P在半圆周上时,也有AP·AC+BP·BD=AP2+BP2=AB2成立,那么:
(1)如图(2)当点P在半圆周外时,结论AP·AC+BP·BD=AB2是否成立?为什么?
(2)如图(3)当点P在切线BE外侧时,你能得到什么结论?将你得到的结论写出来.
[解析] (1)成立.
证明:如图(2),∵∠PCM=∠PDM=900,
∴点C、D在以PM为直径的圆上,
∴AC·AP=AM·MD,BD·BP=BM·BC,
∴AC·AP+BD·BP=AM·MD+BM·BC,
由已知,AM·MD+BM·BC=AB2,
∴AP·AC+BP·BD=AB2.
(2)如图(3),过P作PM⊥AB,交AB的延长线于M,连结AD、BC,
则C、M在以PB为直径的圆上,∴AP·AC=AB·AM,①
D、M在以PA为直径的圆上,∴BP·BD=AB·BM,②
由图象可知:AB=AM-BM,③
由①②③可得:AP·AC-BP·BD=AB·(AM-BM)=AB2.
3、(2006山东济南)如图1,已知中,,.过点作,且,连接交于点.
(1)求的长;
(2)以点为圆心,为半径作⊙A,试判断与⊙A是否相切,并说明理由;
(3)如图2,过点作,垂足为.以点为圆心,为半径作⊙A;以点为圆心,为半径作⊙C.若和的大小是可变化的,并且在变化过程中保持⊙A和⊙C相切,且使点在⊙A的内部,点在⊙A的外部,求和的变化范围.
[解析]
(1)在中,,
.
,.
.
,.
(2)与⊙A相切.
在中,,,
,.
又, HYPERLINK "http://" EMBED Equation.DSMT4 ,
与⊙A相切.
(3)因为,所以的变化范围为.
当⊙A与⊙C外切时,,所以的变化范围为;
当⊙A与⊙C内切时,,所以的变化范围为.
4、(2006江苏盐城)如图,已知:C是以AB为直径的半圆O上一点,CH⊥AB于点H,直线AC与过B点的切线相交于点D,E为CH中点,连接AE并延长交BD于点F,直线CF交直线AB于点G.
(1)求证:点F是BD中点;
(2)求证:CG是⊙O的切线;
(3)若FB=FE=2,求⊙O的半径.
[解析]
(1)证明:∵CH⊥AB,DB⊥AB,∴△AEH∽AFB,△ACE∽△ADF
∴,∵HE=EC,∴BF=FD′
(2)方法一:连接CB、OC,
∵AB是直径,∴∠ACB=90°∵F是BD中点,
∴∠BCF=∠CBF=90°-∠CBA=∠CAB=∠ACO
∴∠OCF=90°,∴CG是⊙O的切线
方法二:可证明△OCF≌△OBF(参照方法一标准得分)
(3)解:由FC=FB=FE得:∠FCE=∠FEC
可证得:FA=FG,且AB=BG
由切割线定理得:(2+FG)2=BG×AG=2BG2
在Rt△BGF中,由勾股定理得:BG2=FG2-BF2
由、得:FG2-4FG-12=0
解之得:FG1=6,FG2=-2(舍去)
∴AB=BG=
∴⊙O半径为2
5、(2006山东烟台)如图,从⊙O外一点A作⊙O的切线AB、AC,切点分别为B、C,且⊙O直经BD=6,连结CD、AO。
(1)求证:CD∥AO;
(2)设CD=x,AO=y,求y与x之间的函数关系式,并写出自变量x的取值范围;
(3)若AO+CD=11,求AB的长。
[解析]
(1)连接BC交OA于E点
∵AB、AC是⊙O的切线,
∴AB=AC, ∠1=∠2
∴AE⊥BC
∴∠OEB=90O
∵BD是⊙O的直径
∴∠DCB=90O
∴∠DCB=∠OEB
∴CD∥AO
(2)∵CD∥AO
∴∠3=∠4
∵AB是⊙O的切线,DB是直径
∴∠DCB=∠ABO=90O
∴△BDC∽△AOB ∴=
∴=
∴y =
∴0(3)由已知和(2)知:
把x、y看作方程z2-11z+18=0的两根
解这个方程 得 z=2或z=9
∴
(舍去)
∴AB===6
6、(2006北京海淀)如图,已知⊙O的直径AB垂直于弦CD于E,连结AD、BD、OC、OD,且OD=5。
(1)若,求CD的长;
(2)若 ∠ADO:∠EDO=4:1,求扇形OAC(阴影部分)的面积(结果保留)。
[解析]
(1)因为AB是⊙O的直径,OD=5
所以∠ADB=90°,AB=10
在Rt△ABD中,
又,所以,所以
因为∠ADB=90°,AB⊥CD
所以
所以
所以
所以
(2)因为AB是⊙O的直径,AB⊥CD
所以
所以∠BAD=∠CDB,∠AOC=∠AOD
因为AO=DO,所以∠BAD=∠ADO
所以∠CDB=∠ADO
设∠ADO=4x,则∠CDB=4x
由∠ADO:∠EDO=4:1,则∠EDO=x
因为∠ADO+∠EDO+∠EDB=90°
所以
所以x=10°
所以∠AOD=180°-(∠OAD+∠ADO)=100°
所以∠AOC=∠AOD=100°
7、(2006湖北十堰)如图,为⊙O的直径,,交于,,.
(1)求证:,并求的长;
(2)延长到,使,连接,那么直线与相切吗?为什么?
[解析]
(1)证明:,,
,.
又,
.
.
.
.
(2)直线与⊙O相切.
理由如下:
连接.
为⊙O的直径,.
.
.
,..
直线与⊙O相切.
8、(2006河北)图1是某学校存放学生自行车的车棚的示意图(尺寸如图所示),车棚顶部是圆柱侧面的一部分,其展开图是矩形.图2是车棚顶部截面的示意图,所在圆的圆心为O.
车棚顶部是用一种帆布覆盖的,求覆盖棚顶的帆布的面积(不考虑接缝等因素,计算结果保留).
[解析] 连结OB,过点O作OE⊥AB,垂足为E,交于F,如图1.
由垂径定理,可知: E是AB中点,F是中点,
∴EF是弓形高 .
∴AE=2,EF=2.
设半径为R米,则OE=(R-2)米.
在Rt△AOE中,由勾股定理,得 R 2=.
解得 R =4.
∵sin∠AOE=, ∴ ∠AOE=60°,
∴∠AOB=120°. ∴ 的长为=.
∴帆布的面积为×60=160(平方米).
2006年中考数学试题分类汇编及解析----圆
A
B
C
P
E
E
A
B
C
P
D
图1
图2
A
F
C
E
B
O
D
O
B
A
·
图2
图1
A
B
2米
4米
·
图1
E
F
O
B
A
(1)与是否相等?为什么?
(2)求由DG、GE和弧ED所围成图形的面积(阴影部分).
[解析] (1) (…1分)
连OD,∵(⊙O的半径),∴ (…2分)
∵⊙O与AC相切于点D,∴
又∵,即,∴,
∴
又∵,∴
(2)连OE,则ODCE为正方形且边长为3
∵
∴
从而
∴阴影部分的面积
=△DCG的面积-(正方形ODCE的面积-扇形ODE的面积) =
2、(2006山东日照)阅读下面的材料:
如图(1),在以AB为直径的半圆O内有一点P,AP、BP的延长线分别交半圆O于点C、D.求证:AP·AC+BP·BD=AB2.
证明:连结AD、BC,过P作PM⊥AB,则∠ADB=∠AMP=90o,
∴点D、M在以AP为直径的圆上;同理:M、C在以BP为直径的圆上.
由割线定理得: AP·AC=AM·AB,BP·BD=BM·BA,
所以,AP·AC+BP·BD=AM·AB+BM·AB=AB·(AM+BM)=AB2.
当点P在半圆周上时,也有AP·AC+BP·BD=AP2+BP2=AB2成立,那么:
(1)如图(2)当点P在半圆周外时,结论AP·AC+BP·BD=AB2是否成立?为什么?
(2)如图(3)当点P在切线BE外侧时,你能得到什么结论?将你得到的结论写出来.
[解析] (1)成立.
证明:如图(2),∵∠PCM=∠PDM=900,
∴点C、D在以PM为直径的圆上,
∴AC·AP=AM·MD,BD·BP=BM·BC,
∴AC·AP+BD·BP=AM·MD+BM·BC,
由已知,AM·MD+BM·BC=AB2,
∴AP·AC+BP·BD=AB2.
(2)如图(3),过P作PM⊥AB,交AB的延长线于M,连结AD、BC,
则C、M在以PB为直径的圆上,∴AP·AC=AB·AM,①
D、M在以PA为直径的圆上,∴BP·BD=AB·BM,②
由图象可知:AB=AM-BM,③
由①②③可得:AP·AC-BP·BD=AB·(AM-BM)=AB2.
3、(2006山东济南)如图1,已知中,,.过点作,且,连接交于点.
(1)求的长;
(2)以点为圆心,为半径作⊙A,试判断与⊙A是否相切,并说明理由;
(3)如图2,过点作,垂足为.以点为圆心,为半径作⊙A;以点为圆心,为半径作⊙C.若和的大小是可变化的,并且在变化过程中保持⊙A和⊙C相切,且使点在⊙A的内部,点在⊙A的外部,求和的变化范围.
[解析]
(1)在中,,
.
,.
.
,.
(2)与⊙A相切.
在中,,,
,.
又, HYPERLINK "http://" EMBED Equation.DSMT4 ,
与⊙A相切.
(3)因为,所以的变化范围为.
当⊙A与⊙C外切时,,所以的变化范围为;
当⊙A与⊙C内切时,,所以的变化范围为.
4、(2006江苏盐城)如图,已知:C是以AB为直径的半圆O上一点,CH⊥AB于点H,直线AC与过B点的切线相交于点D,E为CH中点,连接AE并延长交BD于点F,直线CF交直线AB于点G.
(1)求证:点F是BD中点;
(2)求证:CG是⊙O的切线;
(3)若FB=FE=2,求⊙O的半径.
[解析]
(1)证明:∵CH⊥AB,DB⊥AB,∴△AEH∽AFB,△ACE∽△ADF
∴,∵HE=EC,∴BF=FD′
(2)方法一:连接CB、OC,
∵AB是直径,∴∠ACB=90°∵F是BD中点,
∴∠BCF=∠CBF=90°-∠CBA=∠CAB=∠ACO
∴∠OCF=90°,∴CG是⊙O的切线
方法二:可证明△OCF≌△OBF(参照方法一标准得分)
(3)解:由FC=FB=FE得:∠FCE=∠FEC
可证得:FA=FG,且AB=BG
由切割线定理得:(2+FG)2=BG×AG=2BG2
在Rt△BGF中,由勾股定理得:BG2=FG2-BF2
由、得:FG2-4FG-12=0
解之得:FG1=6,FG2=-2(舍去)
∴AB=BG=
∴⊙O半径为2
5、(2006山东烟台)如图,从⊙O外一点A作⊙O的切线AB、AC,切点分别为B、C,且⊙O直经BD=6,连结CD、AO。
(1)求证:CD∥AO;
(2)设CD=x,AO=y,求y与x之间的函数关系式,并写出自变量x的取值范围;
(3)若AO+CD=11,求AB的长。
[解析]
(1)连接BC交OA于E点
∵AB、AC是⊙O的切线,
∴AB=AC, ∠1=∠2
∴AE⊥BC
∴∠OEB=90O
∵BD是⊙O的直径
∴∠DCB=90O
∴∠DCB=∠OEB
∴CD∥AO
(2)∵CD∥AO
∴∠3=∠4
∵AB是⊙O的切线,DB是直径
∴∠DCB=∠ABO=90O
∴△BDC∽△AOB ∴=
∴=
∴y =
∴0
把x、y看作方程z2-11z+18=0的两根
解这个方程 得 z=2或z=9
∴
(舍去)
∴AB===6
6、(2006北京海淀)如图,已知⊙O的直径AB垂直于弦CD于E,连结AD、BD、OC、OD,且OD=5。
(1)若,求CD的长;
(2)若 ∠ADO:∠EDO=4:1,求扇形OAC(阴影部分)的面积(结果保留)。
[解析]
(1)因为AB是⊙O的直径,OD=5
所以∠ADB=90°,AB=10
在Rt△ABD中,
又,所以,所以
因为∠ADB=90°,AB⊥CD
所以
所以
所以
所以
(2)因为AB是⊙O的直径,AB⊥CD
所以
所以∠BAD=∠CDB,∠AOC=∠AOD
因为AO=DO,所以∠BAD=∠ADO
所以∠CDB=∠ADO
设∠ADO=4x,则∠CDB=4x
由∠ADO:∠EDO=4:1,则∠EDO=x
因为∠ADO+∠EDO+∠EDB=90°
所以
所以x=10°
所以∠AOD=180°-(∠OAD+∠ADO)=100°
所以∠AOC=∠AOD=100°
7、(2006湖北十堰)如图,为⊙O的直径,,交于,,.
(1)求证:,并求的长;
(2)延长到,使,连接,那么直线与相切吗?为什么?
[解析]
(1)证明:,,
,.
又,
.
.
.
.
(2)直线与⊙O相切.
理由如下:
连接.
为⊙O的直径,.
.
.
,..
直线与⊙O相切.
8、(2006河北)图1是某学校存放学生自行车的车棚的示意图(尺寸如图所示),车棚顶部是圆柱侧面的一部分,其展开图是矩形.图2是车棚顶部截面的示意图,所在圆的圆心为O.
车棚顶部是用一种帆布覆盖的,求覆盖棚顶的帆布的面积(不考虑接缝等因素,计算结果保留).
[解析] 连结OB,过点O作OE⊥AB,垂足为E,交于F,如图1.
由垂径定理,可知: E是AB中点,F是中点,
∴EF是弓形高 .
∴AE=2,EF=2.
设半径为R米,则OE=(R-2)米.
在Rt△AOE中,由勾股定理,得 R 2=.
解得 R =4.
∵sin∠AOE=, ∴ ∠AOE=60°,
∴∠AOB=120°. ∴ 的长为=.
∴帆布的面积为×60=160(平方米).
2006年中考数学试题分类汇编及解析----圆
A
B
C
P
E
E
A
B
C
P
D
图1
图2
A
F
C
E
B
O
D
O
B
A
·
图2
图1
A
B
2米
4米
·
图1
E
F
O
B
A
同课章节目录
