北师大版九年级下册 第二章 二次函数课件(共25张PPT)
文档属性
| 名称 | 北师大版九年级下册 第二章 二次函数课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 403.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-09 09:50:41 | ||
图片预览







文档简介
(共25张PPT)
1. 通过对实际问题的分析,体会二次函数的意义.
2. 能画二次函数的图象,通过图象了解二次函数的性质,知道二次函数系数与图象形状和对称轴的关系.
3. 会求二次函数的最大值或最小值,并能确定相应自变量的值,能解决相应的实际问题.
4. 知道二次函数和一元二次方程之间的关系,会利用二次函数的图象求一元二次方程的近似解.
课程标准
单元复习课
本章知识梳理
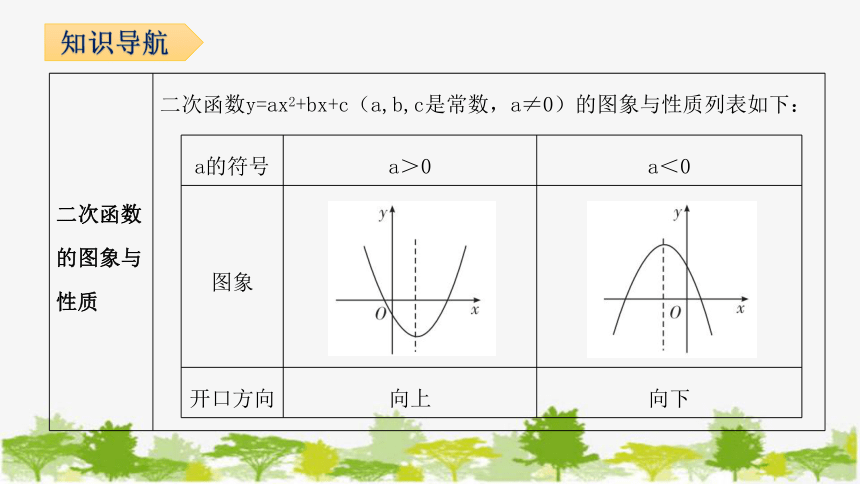
二次函数的图象与性质 二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的图象与性质列表如下:
知识导航
a的符号 a>0 a<0
图象
开口方向 向上 向下
续表
二次函数的图象与性质 二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的图象与性质列表如下:
a的符号 a>0 a<0
对称轴
顶点坐标
增减性
续表
二次函数的图象与性质 二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的图象与性质列表如下:
二次函数的解析式有三种常见形式:
(1)一般式:y=ax2+bx+c(a,b,c是常数,a≠0)
(2)顶点式:y=a(x-h)2+k(a,h,k是常数,a≠0),其中(h,k)为顶点坐标
(3)交点式:y=a(x-x1)(x-x2)(a,x1,x2是常数,a≠0),其中x1,x2是图象与x轴交点的横坐标
a的符号 a>0 a<0
最值
续表
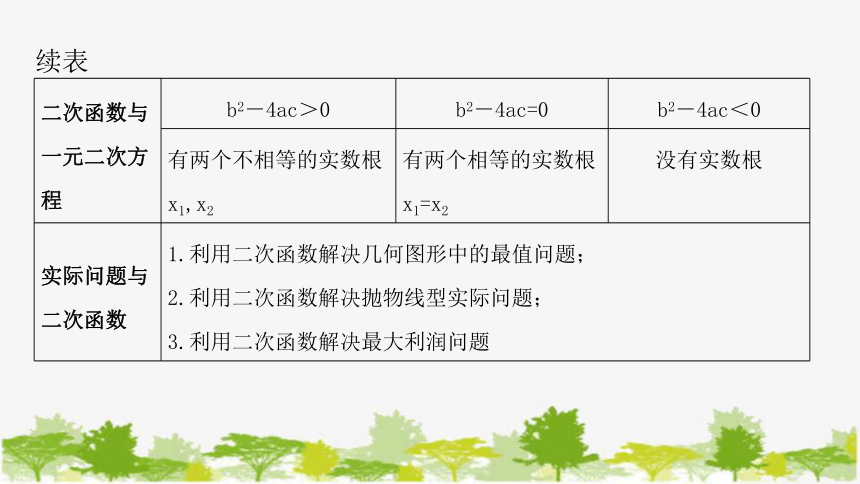
二次函数与一元二次方程 b2-4ac>0 b2-4ac=0 b2-4ac<0
有两个不相等的实数根x1,x2 有两个相等的实数根x1=x2 没有实数根
实际问题与二次函数 1.利用二次函数解决几何图形中的最值问题; 2.利用二次函数解决抛物线型实际问题; 3.利用二次函数解决最大利润问题
专题一 本章易错点例析
第二章 二次函数
目录
01
易错典例
02
过关训练
易错点1:忽视二次项系数不等于0
易错典例
【例1】已知二次函数y=kx2-6x+3的图象与x轴有交点,则k的取值范围是( )
A. k<3 B. k<3且k≠0
C.k≤3 D. k≤3且k≠0
错解:选C.由Δ=(-6)2-4k×3≥0,得k≤3.
错解分析:当k=0时,二次项系数为0,此时原函数不是二次函数,上面的解法忽略了这种情况.
正解:由Δ=(-6)2-4k×3≥0且k≠0,得k≤3且k≠0.
故选D.
过关训练
1.已知二次函数y=(k-2)x2+2x+1的图象与x轴有交点,则k的取值范围是( )
A. k≤3
B. k<3
C. k≤3且k≠2
D. k<3且k≠2
C
易错点2: 求顶点坐标时混淆符号
易错典例
【例2】求二次函数y=-x2+2x-2图象的顶点坐标.
错解:y=-x2+2x-2=-(x-1)2-1.
所以顶点坐标为(-1,-1).
错解分析:二次函数y=a(x-h)2+k的顶点坐标是(h,k),而不是
(-h,k).
正解:顶点坐标为(1,-1).
过关训练
(-2,4)
易错点3: 忽视二次项系数的符号
易错典例
过关训练
3.若二次函数y=ax2+8x+(a-3)的图象最高点的纵坐标为3,则a的值是____________.
-2
易错点4:忽视分类讨论
易错典例
错解分析:在没指明函数的类型时,应分a-2=0和a-2≠0进行
讨论.
正解:①当a-2=0,即a=2时,
函数的解析式为y=-3x+2.
该函数为一次函数,符合题意;
②当a-2≠0时,即a≠2时,
该函数为二次函数.
分下面两种情况:
过关训练
4.若函数y=2mx2+(m+2)x+1的图象与x轴有且只有一个交点,求m的值.
解:①当2m=0,即m=0时,
函数解析式为y=2x+1.
该函数为一次函数,符合题意;
②当2m≠0,即m≠0时,
该函数为二次函数.
∵该函数的图象与x轴有且只有一个交点,
∴Δ=(m+2)2-4×2m×1=0.
解得m1=m2=2.
∴m的值为0或2.
易错点5: 在实际应用中忽略了自变量的取值范围
易错典例
【例5】如图XD2-1-1,依靠一面8 m长的墙,用20 m长的篱笆围成一个矩形场地ABCD.设AD的长为x m,矩形场地的面积为y m2,求面积的最大值.
错解:∵四边形ABCD是矩形,
∴BC=AD=x m.
∴AB=(20-2x)m.
由题意,得y=AB·AD=(20-2x)x=-2x2+20x=-2(x-5)2+50.
∴当x=5时,y有最大值,最大值为50.
错解分析:上面的解法没有考虑到x的取值.当x=5时,AB=20-2x=10,而墙只有8 m,不合题意.
正解:∵四边形ABCD是矩形,
∴BC=AD=x m.
∴AB=(20-2x)m.
由题意,得y=AB·AD=(20-2x)x=-2x2+20x=-2(x-5)2+50.
∵0<20-2x≤8,
∴6≤x<10.
∵-2<0,
∴当x=6时,y有最大值,
y最大值=-2×(6-5)2+50=48.
∴面积的最大值为48 m2.
过关训练
5. 冬奥会期间,某商家进行吉祥物“冰墩墩”纪念品的销售,每个纪念品进价40元.当销售单价定为46元时,每天可售出400个,由于销售火爆,商家决定提价销售.经市场调研发现,销售单价每上涨1元,每天销量减少10个,且规定利润率不得高于50%.设销售单价为x元,当x为多少时,商家每天销售纪念品获得的利润w最大?最大利润是多少元?
解:由题意,得
w=(x-40)[400-10(x-46)]
=-10x2+1 260x-34 400
=-10(x-63)2+5 290.
∵规定利润率不得高于50%,
∴46≤x≤40×(1+50%).
∴46≤x≤60.
∵-10<0,
∴当x=60时,w有最大值,
w最大值=-10×(60-63)2+5 290=5 200.
∴当x=60时,商家每天销售纪念品获得的利润w最大,最大利润是5 200元.
谢 谢
1. 通过对实际问题的分析,体会二次函数的意义.
2. 能画二次函数的图象,通过图象了解二次函数的性质,知道二次函数系数与图象形状和对称轴的关系.
3. 会求二次函数的最大值或最小值,并能确定相应自变量的值,能解决相应的实际问题.
4. 知道二次函数和一元二次方程之间的关系,会利用二次函数的图象求一元二次方程的近似解.
课程标准
单元复习课
本章知识梳理
二次函数的图象与性质 二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的图象与性质列表如下:
知识导航
a的符号 a>0 a<0
图象
开口方向 向上 向下
续表
二次函数的图象与性质 二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的图象与性质列表如下:
a的符号 a>0 a<0
对称轴
顶点坐标
增减性
续表
二次函数的图象与性质 二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的图象与性质列表如下:
二次函数的解析式有三种常见形式:
(1)一般式:y=ax2+bx+c(a,b,c是常数,a≠0)
(2)顶点式:y=a(x-h)2+k(a,h,k是常数,a≠0),其中(h,k)为顶点坐标
(3)交点式:y=a(x-x1)(x-x2)(a,x1,x2是常数,a≠0),其中x1,x2是图象与x轴交点的横坐标
a的符号 a>0 a<0
最值
续表
二次函数与一元二次方程 b2-4ac>0 b2-4ac=0 b2-4ac<0
有两个不相等的实数根x1,x2 有两个相等的实数根x1=x2 没有实数根
实际问题与二次函数 1.利用二次函数解决几何图形中的最值问题; 2.利用二次函数解决抛物线型实际问题; 3.利用二次函数解决最大利润问题
专题一 本章易错点例析
第二章 二次函数
目录
01
易错典例
02
过关训练
易错点1:忽视二次项系数不等于0
易错典例
【例1】已知二次函数y=kx2-6x+3的图象与x轴有交点,则k的取值范围是( )
A. k<3 B. k<3且k≠0
C.k≤3 D. k≤3且k≠0
错解:选C.由Δ=(-6)2-4k×3≥0,得k≤3.
错解分析:当k=0时,二次项系数为0,此时原函数不是二次函数,上面的解法忽略了这种情况.
正解:由Δ=(-6)2-4k×3≥0且k≠0,得k≤3且k≠0.
故选D.
过关训练
1.已知二次函数y=(k-2)x2+2x+1的图象与x轴有交点,则k的取值范围是( )
A. k≤3
B. k<3
C. k≤3且k≠2
D. k<3且k≠2
C
易错点2: 求顶点坐标时混淆符号
易错典例
【例2】求二次函数y=-x2+2x-2图象的顶点坐标.
错解:y=-x2+2x-2=-(x-1)2-1.
所以顶点坐标为(-1,-1).
错解分析:二次函数y=a(x-h)2+k的顶点坐标是(h,k),而不是
(-h,k).
正解:顶点坐标为(1,-1).
过关训练
(-2,4)
易错点3: 忽视二次项系数的符号
易错典例
过关训练
3.若二次函数y=ax2+8x+(a-3)的图象最高点的纵坐标为3,则a的值是____________.
-2
易错点4:忽视分类讨论
易错典例
错解分析:在没指明函数的类型时,应分a-2=0和a-2≠0进行
讨论.
正解:①当a-2=0,即a=2时,
函数的解析式为y=-3x+2.
该函数为一次函数,符合题意;
②当a-2≠0时,即a≠2时,
该函数为二次函数.
分下面两种情况:
过关训练
4.若函数y=2mx2+(m+2)x+1的图象与x轴有且只有一个交点,求m的值.
解:①当2m=0,即m=0时,
函数解析式为y=2x+1.
该函数为一次函数,符合题意;
②当2m≠0,即m≠0时,
该函数为二次函数.
∵该函数的图象与x轴有且只有一个交点,
∴Δ=(m+2)2-4×2m×1=0.
解得m1=m2=2.
∴m的值为0或2.
易错点5: 在实际应用中忽略了自变量的取值范围
易错典例
【例5】如图XD2-1-1,依靠一面8 m长的墙,用20 m长的篱笆围成一个矩形场地ABCD.设AD的长为x m,矩形场地的面积为y m2,求面积的最大值.
错解:∵四边形ABCD是矩形,
∴BC=AD=x m.
∴AB=(20-2x)m.
由题意,得y=AB·AD=(20-2x)x=-2x2+20x=-2(x-5)2+50.
∴当x=5时,y有最大值,最大值为50.
错解分析:上面的解法没有考虑到x的取值.当x=5时,AB=20-2x=10,而墙只有8 m,不合题意.
正解:∵四边形ABCD是矩形,
∴BC=AD=x m.
∴AB=(20-2x)m.
由题意,得y=AB·AD=(20-2x)x=-2x2+20x=-2(x-5)2+50.
∵0<20-2x≤8,
∴6≤x<10.
∵-2<0,
∴当x=6时,y有最大值,
y最大值=-2×(6-5)2+50=48.
∴面积的最大值为48 m2.
过关训练
5. 冬奥会期间,某商家进行吉祥物“冰墩墩”纪念品的销售,每个纪念品进价40元.当销售单价定为46元时,每天可售出400个,由于销售火爆,商家决定提价销售.经市场调研发现,销售单价每上涨1元,每天销量减少10个,且规定利润率不得高于50%.设销售单价为x元,当x为多少时,商家每天销售纪念品获得的利润w最大?最大利润是多少元?
解:由题意,得
w=(x-40)[400-10(x-46)]
=-10x2+1 260x-34 400
=-10(x-63)2+5 290.
∵规定利润率不得高于50%,
∴46≤x≤40×(1+50%).
∴46≤x≤60.
∵-10<0,
∴当x=60时,w有最大值,
w最大值=-10×(60-63)2+5 290=5 200.
∴当x=60时,商家每天销售纪念品获得的利润w最大,最大利润是5 200元.
谢 谢
