24.1.2 垂直于弦的直径选择题练习(含解析)
文档属性
| 名称 | 24.1.2 垂直于弦的直径选择题练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 868.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 20:13:20 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
垂直于弦的直径选择题练习
1.如图,在⊙O中,AB是⊙O直径,弦CD⊥AB于点H.若AH=5,HB=1,则CD的长为( )
A. B. C.2 D.2
2.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,如图1,点M表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心.5米为半径的圆,旦圆心在水面上方,若圆被水面截得的弦AB长为8米,则筒车工作时,盛水桶在水面以下的最大深度为( )
A.1米 B.2米 C.3米 D.4米
3.如图,矩形ABCD中,E,F分别是边AB,BC上的两个动点,将△BEF沿着直线EF作轴对称变换,得到△B′EF,点B′恰好在边AD上,过点D,F,B′作⊙O,连结OF.若OF⊥BC,AB′=CF=6时,则AE=( )
A.3 B.6 C. D.
4.如图是某圆弧形桥洞,水面跨径AB=12米,小明为了计算圆弧所在圆的半径,他在左侧水面D处测得桥洞高CD=AD=1.5米,则圆弧所在圆的半径为( )
A.7.5米 B.米 C.米 D.10米
5.如图,AB是⊙O的直径,弦CD⊥AB于点E,BE=2cm,CD=8cm,则⊙O半径为( )
A.2cm B.3cm C.5cm D.8cm
6.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=10,AE=1,则弦CD的长是( )
A. B.2 C.6 D.8
7.如图,⊙O的直径为10,A、B、C、D是⊙O上的四个动点,且AB=6,CD=8,若点E、F分别是弦AB、CD的中点,则线段EF长度的取值范围是( )
A.1≤EF≤7 B.2≤EF≤5 C.1<EF<7 D.1≤EF≤6
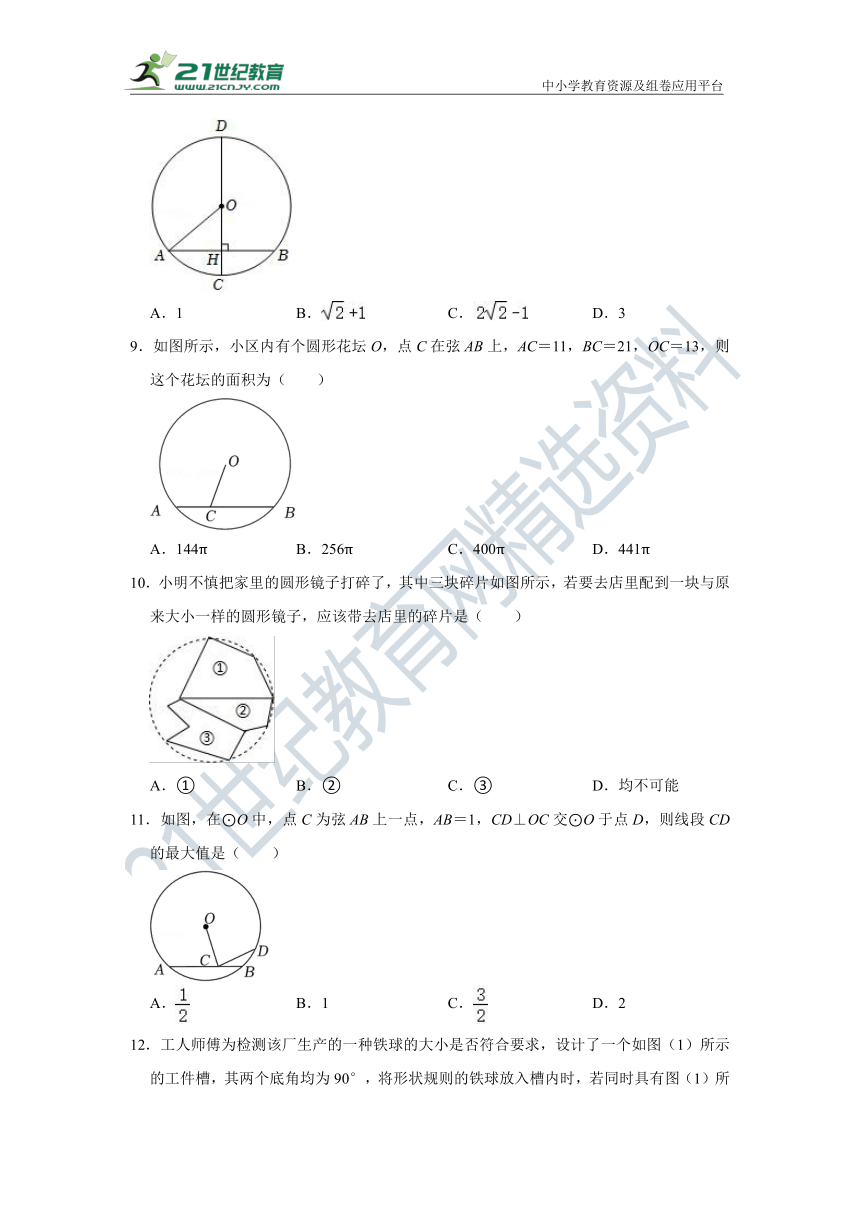
8.如图,AB是⊙O的弦,直径CD⊥AB,交AB于点H,连接OA,若∠A=45°,AB=2,则DH的长度为( )
A.1 B. C. D.3
9.如图所示,小区内有个圆形花坛O,点C在弦AB上,AC=11,BC=21,OC=13,则这个花坛的面积为( )
A.144π B.256π C.400π D.441π
10.小明不慎把家里的圆形镜子打碎了,其中三块碎片如图所示,若要去店里配到一块与原来大小一样的圆形镜子,应该带去店里的碎片是( )
A.① B.② C.③ D.均不可能
11.如图,在⊙O中,点C为弦AB上一点,AB=1,CD⊥OC交⊙O于点D,则线段CD的最大值是( )
A. B.1 C. D.2
12.工人师傅为检测该厂生产的一种铁球的大小是否符合要求,设计了一个如图(1)所示的工件槽,其两个底角均为90°,将形状规则的铁球放入槽内时,若同时具有图(1)所示的A、B、E三个接触点,该球的大小就符合要求.图(2)是过球心及A、B、E三点的截面示意图,已知⊙O的直径就是铁球的直径,AB是⊙O的弦,CD切⊙O于点E,AC⊥CD、BD⊥CD,若CD=16cm,AC=BD=4cm,则这种铁球的直径为( )
A.10cm B.15cm C.20cm D.24cm
13.如图,正方形ABCD和正方形BEFG的顶点分别在半圆O的直径和圆周上,若BG=4,则半圆O的半径是( )
A.4+ B.9 C.4 D.6
14.如图,CD是圆O的弦,直径AB⊥CD,垂足为E,若AB=12,BE=3,则四边形ACBD的面积为( )
A.36 B.24 C.18 D.72
15.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,若BE=CD=8,则⊙O的半径的长是( )
A.5 B.4 C.3 D.2
16.如图,在⊙O中,弦AB=5,点C在AB上移动,连结OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为( )
A.5 B.2.5 C.3 D.2
17.如图,在⊙O中,OD⊥AB于点D,AD的长为3cm,则弦AB的长为( )
A.4cm B.6cm C.8cm D.10cm
18.如图,AB是⊙O的直径,弦CD⊥AB,垂足为P.若CD=AP=8,则⊙O的半径为( )
A.10 B.8 C.5 D.3
19.如图,一个圆柱形的玻璃水杯,将其横放,截面是个半径为5cm的圆,杯内水面宽AB=8cm,则水深CD是( )
A.3cm B.2cm C. D.
20.如图,⊙O的半径为2,AB,CD是互相垂直的两条直径,点P是⊙O上任意一点(P与A,B,C,D不重合),过点P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,在点P运动的过程中,OQ的长度为( )
A.先变小后变大 B.变小
C.不能确定 D.不变
参考答案
1.如图,在⊙O中,AB是⊙O直径,弦CD⊥AB于点H.若AH=5,HB=1,则CD的长为( )
A. B. C.2 D.2
解:连接OD,
∵AB是⊙O直径,弦CD⊥AB,
∴DH=CD,
∵AH=5,HB=1,
∴AB=AH=HB=6,
∴OD=OA=3,
∴OH=AH﹣OA=2,
在Rt△ODH中,DH===,
∴CD=2DH=2,
故选:C.
2.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,如图1,点M表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心.5米为半径的圆,旦圆心在水面上方,若圆被水面截得的弦AB长为8米,则筒车工作时,盛水桶在水面以下的最大深度为( )
A.1米 B.2米 C.3米 D.4米
解:过O点作半径OD⊥AB于E,如图,
∴AE=BE=AB=×8=4,
在Rt△AEO中,OE==3,
∴ED=OD﹣OE=5﹣3=2(m),
答:筒车工作时,盛水桶在水面以下的最大深度为2m.
故选:B.
3.如图,矩形ABCD中,E,F分别是边AB,BC上的两个动点,将△BEF沿着直线EF作轴对称变换,得到△B′EF,点B′恰好在边AD上,过点D,F,B′作⊙O,连结OF.若OF⊥BC,AB′=CF=6时,则AE=( )
A.3 B.6 C. D.
解:延长FO交AD于G,
∵OF⊥BC,AD∥BC,
∴OG⊥AD,
∴GB′=GD,
∵四边形ABCD是矩形,
∴BC=AD,∠C=∠D=90°,
∴四边形FCDG是矩形,
∴GB′=GD=FC=6,
∴BC=AD=GB′+GD+AB′=6+6+6=18,
∴BF=BC﹣FC=18﹣6=12,
∵△BEF和△B′EF关于EF对称,
∴FB′=FB=12,EB′=EB,
∵FG2=FB′2﹣GB′2,
∴FG2=122﹣62=108,
∴FG=6,
∴AB=FG=6,
令AE=x,则EB′=EB=6﹣x,
∵EB′2=EA2+B′A2,
∴=x2+62,
∴x=2,
∴AE=2.
故选:D.
4.如图是某圆弧形桥洞,水面跨径AB=12米,小明为了计算圆弧所在圆的半径,他在左侧水面D处测得桥洞高CD=AD=1.5米,则圆弧所在圆的半径为( )
A.7.5米 B.米 C.米 D.10米
解:如图,取圆心O,连接OB,OC,BC,AC,
∵∠ADC=90°,AD=CD=1.5,
∴∠A=45°,BD=12﹣1.5=10.5,
∴∠O=2∠A=90°,
设半径为r米,则BC=r米,
在Rt△BCD中,根据勾股定理得,
CD2+BD2=BC2,
即1.52+10.52=(r)2,
解得r=7.5,
∴圆弧所在圆的半径7.5米.
故选:A.
5.如图,AB是⊙O的直径,弦CD⊥AB于点E,BE=2cm,CD=8cm,则⊙O半径为( )
A.2cm B.3cm C.5cm D.8cm
解:设⊙O半径为Rcm,则OE=(R﹣2)cm,OC=Rcm,
∵AB⊥CD,CD=8cm,AB过圆心O,
∴CE=DE=4cm,∠OEC=90°,
由勾股定理得:OC2=CE2+OE2,
∴R2=42+(R﹣2)2,
解得:R=5,
即⊙O的半径为5cm,
故选:C.
6.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=10,AE=1,则弦CD的长是( )
A. B.2 C.6 D.8
解:连接OC,
∵AB是⊙O的直径,弦CD⊥AB,
∴CD=2CE,∠OEC=90°,
∵AB=10,AE=1,
∴OC=5,OE=5﹣1=4,
在Rt△COE中,CE==3,
∴CD=2CE=6.
故选:C.
7.如图,⊙O的直径为10,A、B、C、D是⊙O上的四个动点,且AB=6,CD=8,若点E、F分别是弦AB、CD的中点,则线段EF长度的取值范围是( )
A.1≤EF≤7 B.2≤EF≤5 C.1<EF<7 D.1≤EF≤6
解:连接OE、OF、OA、OC,如图所示:
∵⊙O的直径为10,
∴OA=OC=5,
∵点E、F分别是弦AB、CD的中点,AB=6,CD=8,
∴OE⊥AB,OF⊥CD,AE=AB=3,CF=CD=4,
∴OE==4,OF==3,
当AB∥CD时,E、O、F三点共线,
当AB、CD位于O的同侧时,线段EF的长度最短=OE﹣OF=1,
当AB、CD位于O的两侧时,线段EF的长度最长=OE+OF=7,
∴线段EF的长度的取值范围是1≤EF≤7,
故选:A.
8.如图,AB是⊙O的弦,直径CD⊥AB,交AB于点H,连接OA,若∠A=45°,AB=2,则DH的长度为( )
A.1 B. C. D.3
解:∵直径CD⊥AB,AB=2,
∴AH=AB=1,
在Rt△AHO中,∠A=45°,
∴AH=OH=1,
∴AO=DO=,
∴DH=DO+OH=+1.
故选:B.
9.如图所示,小区内有个圆形花坛O,点C在弦AB上,AC=11,BC=21,OC=13,则这个花坛的面积为( )
A.144π B.256π C.400π D.441π
解:如图,连接OB,过点O作OD⊥AB于D,
∵OD⊥AB,OD过圆心,AB是弦,
∴AD=BD=AB=(AC+BC)=×(11+21)=16,
∴CD=BC﹣BD=21﹣16=5,
在Rt△COD中,OD2=OC2﹣CD2=132﹣52=144,
在Rt△BOD中,OB2=OD2+BD2=144+256=400,
∴S⊙O=π×OB2=400π,
即这个花坛的面积为400π.
故选:C.
10.小明不慎把家里的圆形镜子打碎了,其中三块碎片如图所示,若要去店里配到一块与原来大小一样的圆形镜子,应该带去店里的碎片是( )
A.① B.② C.③ D.均不可能
解:第①块出现两条完整的弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.
故选:A.
11.如图,在⊙O中,点C为弦AB上一点,AB=1,CD⊥OC交⊙O于点D,则线段CD的最大值是( )
A. B.1 C. D.2
解:连接OD,
∵CD⊥OC交⊙O于点D,
∴△OCD是直角三角形,
根据勾股定理得CD=,
∵半径OD是定值,
∴当OC⊥AB时,线段OC最小,此时D与B重合,CD=,
∵OC⊥AB,
∴AC=BC=AB=,
∴CD==BC=.
故选:A.
12.工人师傅为检测该厂生产的一种铁球的大小是否符合要求,设计了一个如图(1)所示的工件槽,其两个底角均为90°,将形状规则的铁球放入槽内时,若同时具有图(1)所示的A、B、E三个接触点,该球的大小就符合要求.图(2)是过球心及A、B、E三点的截面示意图,已知⊙O的直径就是铁球的直径,AB是⊙O的弦,CD切⊙O于点E,AC⊥CD、BD⊥CD,若CD=16cm,AC=BD=4cm,则这种铁球的直径为( )
A.10cm B.15cm C.20cm D.24cm
解:如图,连接OE,交AB于点F,连接OA,
∵AC⊥CD、BD⊥CD,
∴AC∥BD,
∵AC=BD=4cm,
∴四边形ACDB是平行四边形,
∴四边形ACDB是矩形,
∴AB∥CD,AB=CD=16cm,
∵CD切⊙O于点E,
∴OE⊥CD,
∴OE⊥AB,
∴四边形EFBD是矩形,AF=AB=×16=8(cm),
∴EF=BD=4cm,
设⊙O的半径为rcm,则OA=rcm,OF=OE﹣EF=(r﹣4)cm,
在Rt△AOF中,OA2=AF2+OF2,
∴r2=82+(r﹣4)2,
解得:r=10,
∴这种铁球的直径为20cm,
故选:C.
13.如图,正方形ABCD和正方形BEFG的顶点分别在半圆O的直径和圆周上,若BG=4,则半圆O的半径是( )
A.4+ B.9 C.4 D.6
解:连接OC,OF,
设OB=x,
∵四边形ABCD是正方形且顶点D和C在圆上,
∴AB=BC=2x,∠OBC=90°,
∵BG=4,四边形BEFG是正方形,
∴OE=x+4,EF=BE=BG=4,∠FEB=90°,
在Rt△BCO中,OC=,
在Rt△FEO中,OF=,
∵OF=OC,
∴5x2=x2+8x+32,
解得x=4或x=﹣2(舍去)
当x=4时,OC=4,
则半圆O的半径是4.
故选:C.
14.如图,CD是圆O的弦,直径AB⊥CD,垂足为E,若AB=12,BE=3,则四边形ACBD的面积为( )
A.36 B.24 C.18 D.72
解:如图,连接OC,
∵AB=12,BE=3,
∴OB=OC=6,OE=3,
∵AB⊥CD,
在Rt△COE中,EC=,
∴CD=2CE=6,
∴四边形ACBD的面积=.
故选:A.
15.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,若BE=CD=8,则⊙O的半径的长是( )
A.5 B.4 C.3 D.2
解:连接OC,
设⊙O的半径为R,则OE=8﹣R,
∵CD⊥AB,AB过圆心O,CD=8,
∴∠OEC=90°,CE=DE=4,
由勾股定理得:OC2=CE2+OE2,
R2=42+(8﹣R)2,
解得:R=5,
即⊙O的半径长是5,
故选:A.
16.如图,在⊙O中,弦AB=5,点C在AB上移动,连结OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为( )
A.5 B.2.5 C.3 D.2
解:连接OD,如图,
∵CD⊥OC,
∴∠DCO=90°,
∴CD=,
当OC的值最小时,CD的值最大,
而OC⊥AB时,OC最小,此时D、B两点重合,
∴CD=CB=AB=×5=2.5,
即CD的最大值为2.5,
故选:B.
17.如图,在⊙O中,OD⊥AB于点D,AD的长为3cm,则弦AB的长为( )
A.4cm B.6cm C.8cm D.10cm
解;∵OD⊥AB,AD=3cm,
∴AB=2AD=6cm.
故选:B.
18.如图,AB是⊙O的直径,弦CD⊥AB,垂足为P.若CD=AP=8,则⊙O的半径为( )
A.10 B.8 C.5 D.3
解:连接OC,
∵AB⊥CD,AB过圆心O,CD=8,
∴CP=DP=4,
设⊙O的半径为R,
∵AP=8,
∴OP=8﹣R,
在Rt△COP中,由勾股定理得:CP2+OP2=OC2,
即(8﹣R)2+42=R2,
解得:R=5,
∴⊙O的半径为5,
故选:C.
19.如图,一个圆柱形的玻璃水杯,将其横放,截面是个半径为5cm的圆,杯内水面宽AB=8cm,则水深CD是( )
A.3cm B.2cm C. D.
解:如图,连接OA、OC,
则OC⊥AB,
∴AC=AB=4(cm),
在Rt△OAC中,OC===3(cm),
∴CD=5﹣3=2(cm).
故选:B.
20.如图,⊙O的半径为2,AB,CD是互相垂直的两条直径,点P是⊙O上任意一点(P与A,B,C,D不重合),过点P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,在点P运动的过程中,OQ的长度为( )
A.先变小后变大 B.变小
C.不能确定 D.不变
解:连接OP,OQ,
∵AB⊥CD,PM⊥OA,PN⊥OD,
∴∠MON=∠PMO=∠PNO=90°,
∴四边形PMON是矩形,
∴MN=OP,
∵∠MON=90°,Q为MN中点,
∴OQ=MN=OP,
∵OP是半径为定值,
∴OQ的长不变.
故选:D.
垂直于弦的直径选择题练习
1.如图,在⊙O中,AB是⊙O直径,弦CD⊥AB于点H.若AH=5,HB=1,则CD的长为( )
A. B. C.2 D.2
2.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,如图1,点M表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心.5米为半径的圆,旦圆心在水面上方,若圆被水面截得的弦AB长为8米,则筒车工作时,盛水桶在水面以下的最大深度为( )
A.1米 B.2米 C.3米 D.4米
3.如图,矩形ABCD中,E,F分别是边AB,BC上的两个动点,将△BEF沿着直线EF作轴对称变换,得到△B′EF,点B′恰好在边AD上,过点D,F,B′作⊙O,连结OF.若OF⊥BC,AB′=CF=6时,则AE=( )
A.3 B.6 C. D.
4.如图是某圆弧形桥洞,水面跨径AB=12米,小明为了计算圆弧所在圆的半径,他在左侧水面D处测得桥洞高CD=AD=1.5米,则圆弧所在圆的半径为( )
A.7.5米 B.米 C.米 D.10米
5.如图,AB是⊙O的直径,弦CD⊥AB于点E,BE=2cm,CD=8cm,则⊙O半径为( )
A.2cm B.3cm C.5cm D.8cm
6.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=10,AE=1,则弦CD的长是( )
A. B.2 C.6 D.8
7.如图,⊙O的直径为10,A、B、C、D是⊙O上的四个动点,且AB=6,CD=8,若点E、F分别是弦AB、CD的中点,则线段EF长度的取值范围是( )
A.1≤EF≤7 B.2≤EF≤5 C.1<EF<7 D.1≤EF≤6
8.如图,AB是⊙O的弦,直径CD⊥AB,交AB于点H,连接OA,若∠A=45°,AB=2,则DH的长度为( )
A.1 B. C. D.3
9.如图所示,小区内有个圆形花坛O,点C在弦AB上,AC=11,BC=21,OC=13,则这个花坛的面积为( )
A.144π B.256π C.400π D.441π
10.小明不慎把家里的圆形镜子打碎了,其中三块碎片如图所示,若要去店里配到一块与原来大小一样的圆形镜子,应该带去店里的碎片是( )
A.① B.② C.③ D.均不可能
11.如图,在⊙O中,点C为弦AB上一点,AB=1,CD⊥OC交⊙O于点D,则线段CD的最大值是( )
A. B.1 C. D.2
12.工人师傅为检测该厂生产的一种铁球的大小是否符合要求,设计了一个如图(1)所示的工件槽,其两个底角均为90°,将形状规则的铁球放入槽内时,若同时具有图(1)所示的A、B、E三个接触点,该球的大小就符合要求.图(2)是过球心及A、B、E三点的截面示意图,已知⊙O的直径就是铁球的直径,AB是⊙O的弦,CD切⊙O于点E,AC⊥CD、BD⊥CD,若CD=16cm,AC=BD=4cm,则这种铁球的直径为( )
A.10cm B.15cm C.20cm D.24cm
13.如图,正方形ABCD和正方形BEFG的顶点分别在半圆O的直径和圆周上,若BG=4,则半圆O的半径是( )
A.4+ B.9 C.4 D.6
14.如图,CD是圆O的弦,直径AB⊥CD,垂足为E,若AB=12,BE=3,则四边形ACBD的面积为( )
A.36 B.24 C.18 D.72
15.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,若BE=CD=8,则⊙O的半径的长是( )
A.5 B.4 C.3 D.2
16.如图,在⊙O中,弦AB=5,点C在AB上移动,连结OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为( )
A.5 B.2.5 C.3 D.2
17.如图,在⊙O中,OD⊥AB于点D,AD的长为3cm,则弦AB的长为( )
A.4cm B.6cm C.8cm D.10cm
18.如图,AB是⊙O的直径,弦CD⊥AB,垂足为P.若CD=AP=8,则⊙O的半径为( )
A.10 B.8 C.5 D.3
19.如图,一个圆柱形的玻璃水杯,将其横放,截面是个半径为5cm的圆,杯内水面宽AB=8cm,则水深CD是( )
A.3cm B.2cm C. D.
20.如图,⊙O的半径为2,AB,CD是互相垂直的两条直径,点P是⊙O上任意一点(P与A,B,C,D不重合),过点P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,在点P运动的过程中,OQ的长度为( )
A.先变小后变大 B.变小
C.不能确定 D.不变
参考答案
1.如图,在⊙O中,AB是⊙O直径,弦CD⊥AB于点H.若AH=5,HB=1,则CD的长为( )
A. B. C.2 D.2
解:连接OD,
∵AB是⊙O直径,弦CD⊥AB,
∴DH=CD,
∵AH=5,HB=1,
∴AB=AH=HB=6,
∴OD=OA=3,
∴OH=AH﹣OA=2,
在Rt△ODH中,DH===,
∴CD=2DH=2,
故选:C.
2.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,如图1,点M表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心.5米为半径的圆,旦圆心在水面上方,若圆被水面截得的弦AB长为8米,则筒车工作时,盛水桶在水面以下的最大深度为( )
A.1米 B.2米 C.3米 D.4米
解:过O点作半径OD⊥AB于E,如图,
∴AE=BE=AB=×8=4,
在Rt△AEO中,OE==3,
∴ED=OD﹣OE=5﹣3=2(m),
答:筒车工作时,盛水桶在水面以下的最大深度为2m.
故选:B.
3.如图,矩形ABCD中,E,F分别是边AB,BC上的两个动点,将△BEF沿着直线EF作轴对称变换,得到△B′EF,点B′恰好在边AD上,过点D,F,B′作⊙O,连结OF.若OF⊥BC,AB′=CF=6时,则AE=( )
A.3 B.6 C. D.
解:延长FO交AD于G,
∵OF⊥BC,AD∥BC,
∴OG⊥AD,
∴GB′=GD,
∵四边形ABCD是矩形,
∴BC=AD,∠C=∠D=90°,
∴四边形FCDG是矩形,
∴GB′=GD=FC=6,
∴BC=AD=GB′+GD+AB′=6+6+6=18,
∴BF=BC﹣FC=18﹣6=12,
∵△BEF和△B′EF关于EF对称,
∴FB′=FB=12,EB′=EB,
∵FG2=FB′2﹣GB′2,
∴FG2=122﹣62=108,
∴FG=6,
∴AB=FG=6,
令AE=x,则EB′=EB=6﹣x,
∵EB′2=EA2+B′A2,
∴=x2+62,
∴x=2,
∴AE=2.
故选:D.
4.如图是某圆弧形桥洞,水面跨径AB=12米,小明为了计算圆弧所在圆的半径,他在左侧水面D处测得桥洞高CD=AD=1.5米,则圆弧所在圆的半径为( )
A.7.5米 B.米 C.米 D.10米
解:如图,取圆心O,连接OB,OC,BC,AC,
∵∠ADC=90°,AD=CD=1.5,
∴∠A=45°,BD=12﹣1.5=10.5,
∴∠O=2∠A=90°,
设半径为r米,则BC=r米,
在Rt△BCD中,根据勾股定理得,
CD2+BD2=BC2,
即1.52+10.52=(r)2,
解得r=7.5,
∴圆弧所在圆的半径7.5米.
故选:A.
5.如图,AB是⊙O的直径,弦CD⊥AB于点E,BE=2cm,CD=8cm,则⊙O半径为( )
A.2cm B.3cm C.5cm D.8cm
解:设⊙O半径为Rcm,则OE=(R﹣2)cm,OC=Rcm,
∵AB⊥CD,CD=8cm,AB过圆心O,
∴CE=DE=4cm,∠OEC=90°,
由勾股定理得:OC2=CE2+OE2,
∴R2=42+(R﹣2)2,
解得:R=5,
即⊙O的半径为5cm,
故选:C.
6.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=10,AE=1,则弦CD的长是( )
A. B.2 C.6 D.8
解:连接OC,
∵AB是⊙O的直径,弦CD⊥AB,
∴CD=2CE,∠OEC=90°,
∵AB=10,AE=1,
∴OC=5,OE=5﹣1=4,
在Rt△COE中,CE==3,
∴CD=2CE=6.
故选:C.
7.如图,⊙O的直径为10,A、B、C、D是⊙O上的四个动点,且AB=6,CD=8,若点E、F分别是弦AB、CD的中点,则线段EF长度的取值范围是( )
A.1≤EF≤7 B.2≤EF≤5 C.1<EF<7 D.1≤EF≤6
解:连接OE、OF、OA、OC,如图所示:
∵⊙O的直径为10,
∴OA=OC=5,
∵点E、F分别是弦AB、CD的中点,AB=6,CD=8,
∴OE⊥AB,OF⊥CD,AE=AB=3,CF=CD=4,
∴OE==4,OF==3,
当AB∥CD时,E、O、F三点共线,
当AB、CD位于O的同侧时,线段EF的长度最短=OE﹣OF=1,
当AB、CD位于O的两侧时,线段EF的长度最长=OE+OF=7,
∴线段EF的长度的取值范围是1≤EF≤7,
故选:A.
8.如图,AB是⊙O的弦,直径CD⊥AB,交AB于点H,连接OA,若∠A=45°,AB=2,则DH的长度为( )
A.1 B. C. D.3
解:∵直径CD⊥AB,AB=2,
∴AH=AB=1,
在Rt△AHO中,∠A=45°,
∴AH=OH=1,
∴AO=DO=,
∴DH=DO+OH=+1.
故选:B.
9.如图所示,小区内有个圆形花坛O,点C在弦AB上,AC=11,BC=21,OC=13,则这个花坛的面积为( )
A.144π B.256π C.400π D.441π
解:如图,连接OB,过点O作OD⊥AB于D,
∵OD⊥AB,OD过圆心,AB是弦,
∴AD=BD=AB=(AC+BC)=×(11+21)=16,
∴CD=BC﹣BD=21﹣16=5,
在Rt△COD中,OD2=OC2﹣CD2=132﹣52=144,
在Rt△BOD中,OB2=OD2+BD2=144+256=400,
∴S⊙O=π×OB2=400π,
即这个花坛的面积为400π.
故选:C.
10.小明不慎把家里的圆形镜子打碎了,其中三块碎片如图所示,若要去店里配到一块与原来大小一样的圆形镜子,应该带去店里的碎片是( )
A.① B.② C.③ D.均不可能
解:第①块出现两条完整的弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.
故选:A.
11.如图,在⊙O中,点C为弦AB上一点,AB=1,CD⊥OC交⊙O于点D,则线段CD的最大值是( )
A. B.1 C. D.2
解:连接OD,
∵CD⊥OC交⊙O于点D,
∴△OCD是直角三角形,
根据勾股定理得CD=,
∵半径OD是定值,
∴当OC⊥AB时,线段OC最小,此时D与B重合,CD=,
∵OC⊥AB,
∴AC=BC=AB=,
∴CD==BC=.
故选:A.
12.工人师傅为检测该厂生产的一种铁球的大小是否符合要求,设计了一个如图(1)所示的工件槽,其两个底角均为90°,将形状规则的铁球放入槽内时,若同时具有图(1)所示的A、B、E三个接触点,该球的大小就符合要求.图(2)是过球心及A、B、E三点的截面示意图,已知⊙O的直径就是铁球的直径,AB是⊙O的弦,CD切⊙O于点E,AC⊥CD、BD⊥CD,若CD=16cm,AC=BD=4cm,则这种铁球的直径为( )
A.10cm B.15cm C.20cm D.24cm
解:如图,连接OE,交AB于点F,连接OA,
∵AC⊥CD、BD⊥CD,
∴AC∥BD,
∵AC=BD=4cm,
∴四边形ACDB是平行四边形,
∴四边形ACDB是矩形,
∴AB∥CD,AB=CD=16cm,
∵CD切⊙O于点E,
∴OE⊥CD,
∴OE⊥AB,
∴四边形EFBD是矩形,AF=AB=×16=8(cm),
∴EF=BD=4cm,
设⊙O的半径为rcm,则OA=rcm,OF=OE﹣EF=(r﹣4)cm,
在Rt△AOF中,OA2=AF2+OF2,
∴r2=82+(r﹣4)2,
解得:r=10,
∴这种铁球的直径为20cm,
故选:C.
13.如图,正方形ABCD和正方形BEFG的顶点分别在半圆O的直径和圆周上,若BG=4,则半圆O的半径是( )
A.4+ B.9 C.4 D.6
解:连接OC,OF,
设OB=x,
∵四边形ABCD是正方形且顶点D和C在圆上,
∴AB=BC=2x,∠OBC=90°,
∵BG=4,四边形BEFG是正方形,
∴OE=x+4,EF=BE=BG=4,∠FEB=90°,
在Rt△BCO中,OC=,
在Rt△FEO中,OF=,
∵OF=OC,
∴5x2=x2+8x+32,
解得x=4或x=﹣2(舍去)
当x=4时,OC=4,
则半圆O的半径是4.
故选:C.
14.如图,CD是圆O的弦,直径AB⊥CD,垂足为E,若AB=12,BE=3,则四边形ACBD的面积为( )
A.36 B.24 C.18 D.72
解:如图,连接OC,
∵AB=12,BE=3,
∴OB=OC=6,OE=3,
∵AB⊥CD,
在Rt△COE中,EC=,
∴CD=2CE=6,
∴四边形ACBD的面积=.
故选:A.
15.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,若BE=CD=8,则⊙O的半径的长是( )
A.5 B.4 C.3 D.2
解:连接OC,
设⊙O的半径为R,则OE=8﹣R,
∵CD⊥AB,AB过圆心O,CD=8,
∴∠OEC=90°,CE=DE=4,
由勾股定理得:OC2=CE2+OE2,
R2=42+(8﹣R)2,
解得:R=5,
即⊙O的半径长是5,
故选:A.
16.如图,在⊙O中,弦AB=5,点C在AB上移动,连结OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为( )
A.5 B.2.5 C.3 D.2
解:连接OD,如图,
∵CD⊥OC,
∴∠DCO=90°,
∴CD=,
当OC的值最小时,CD的值最大,
而OC⊥AB时,OC最小,此时D、B两点重合,
∴CD=CB=AB=×5=2.5,
即CD的最大值为2.5,
故选:B.
17.如图,在⊙O中,OD⊥AB于点D,AD的长为3cm,则弦AB的长为( )
A.4cm B.6cm C.8cm D.10cm
解;∵OD⊥AB,AD=3cm,
∴AB=2AD=6cm.
故选:B.
18.如图,AB是⊙O的直径,弦CD⊥AB,垂足为P.若CD=AP=8,则⊙O的半径为( )
A.10 B.8 C.5 D.3
解:连接OC,
∵AB⊥CD,AB过圆心O,CD=8,
∴CP=DP=4,
设⊙O的半径为R,
∵AP=8,
∴OP=8﹣R,
在Rt△COP中,由勾股定理得:CP2+OP2=OC2,
即(8﹣R)2+42=R2,
解得:R=5,
∴⊙O的半径为5,
故选:C.
19.如图,一个圆柱形的玻璃水杯,将其横放,截面是个半径为5cm的圆,杯内水面宽AB=8cm,则水深CD是( )
A.3cm B.2cm C. D.
解:如图,连接OA、OC,
则OC⊥AB,
∴AC=AB=4(cm),
在Rt△OAC中,OC===3(cm),
∴CD=5﹣3=2(cm).
故选:B.
20.如图,⊙O的半径为2,AB,CD是互相垂直的两条直径,点P是⊙O上任意一点(P与A,B,C,D不重合),过点P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,在点P运动的过程中,OQ的长度为( )
A.先变小后变大 B.变小
C.不能确定 D.不变
解:连接OP,OQ,
∵AB⊥CD,PM⊥OA,PN⊥OD,
∴∠MON=∠PMO=∠PNO=90°,
∴四边形PMON是矩形,
∴MN=OP,
∵∠MON=90°,Q为MN中点,
∴OQ=MN=OP,
∵OP是半径为定值,
∴OQ的长不变.
故选:D.
同课章节目录
