人教版九年级数学上册 扇形面积计算 选择题专项练习(含答案)
文档属性
| 名称 | 人教版九年级数学上册 扇形面积计算 选择题专项练习(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 11:42:52 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
扇形面积计算选择题专项练习
1.把一个圆的面积按3:5剪成两个扇形,已知大扇形的面积比小扇形多104平方厘米,大扇形的面积是( )平方厘米.
A.416 B.260 C.156 D.208
2.如图,扇形AOB圆心角为直角,OA=10,点C在上,以OA,CA为邻边构造 ACDO,边CD交OB于点E,若OE=8,则图中两块阴影部分的面积和为( )
A.10π﹣8 B.5π﹣8 C.25π﹣64 D.50π﹣64
3.如图,在菱形ABCD中,点E是BC的中点,以C为圆心、CE为半径作弧,交CD于点F,连接AE、AF.若AB=12,∠B=60°,则阴影部分的面积为( )
A.18﹣12π B.36﹣6π C.36﹣12π D.18﹣6π
4.如图,正方形ABCD的边长为2,O为对角线的交点,点E,F分别为BC,AD的中点.以C为圆心,BC为半径作圆弧BD,再分别以E,F为圆心,BE为半径作圆弧BO,OD,则图中阴影部分的面积为( )
A.π﹣1 B.π﹣3 C.π﹣2 D.4﹣π
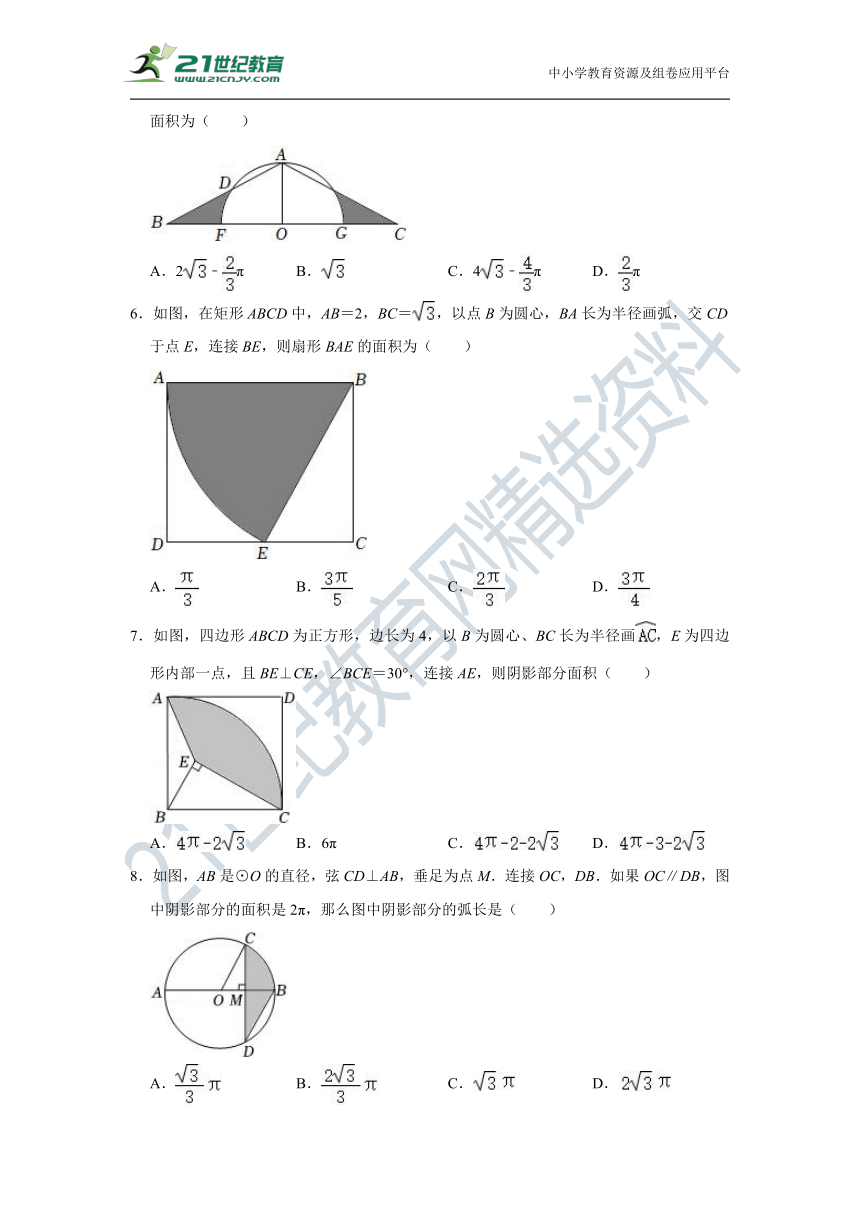
5.如图,在△ABC中,AB=AC=4,∠BAC=120°,AO是△ABC的中线.以O为圆心,OA长为半径作半圆,分别交AB,AC于点D,E,交BC于点F,G.则图中阴影部分的面积为( )
A.2﹣π B. C.4﹣π D.π
6.如图,在矩形ABCD中,AB=2,BC=,以点B为圆心,BA长为半径画弧,交CD于点E,连接BE,则扇形BAE的面积为( )
A. B. C. D.
7.如图,四边形ABCD为正方形,边长为4,以B为圆心、BC长为半径画,E为四边形内部一点,且BE⊥CE,∠BCE=30°,连接AE,则阴影部分面积( )
A. B.6π C. D.
8.如图,AB是⊙O的直径,弦CD⊥AB,垂足为点M.连接OC,DB.如果OC∥DB,图中阴影部分的面积是2π,那么图中阴影部分的弧长是( )
A. B. C. D.
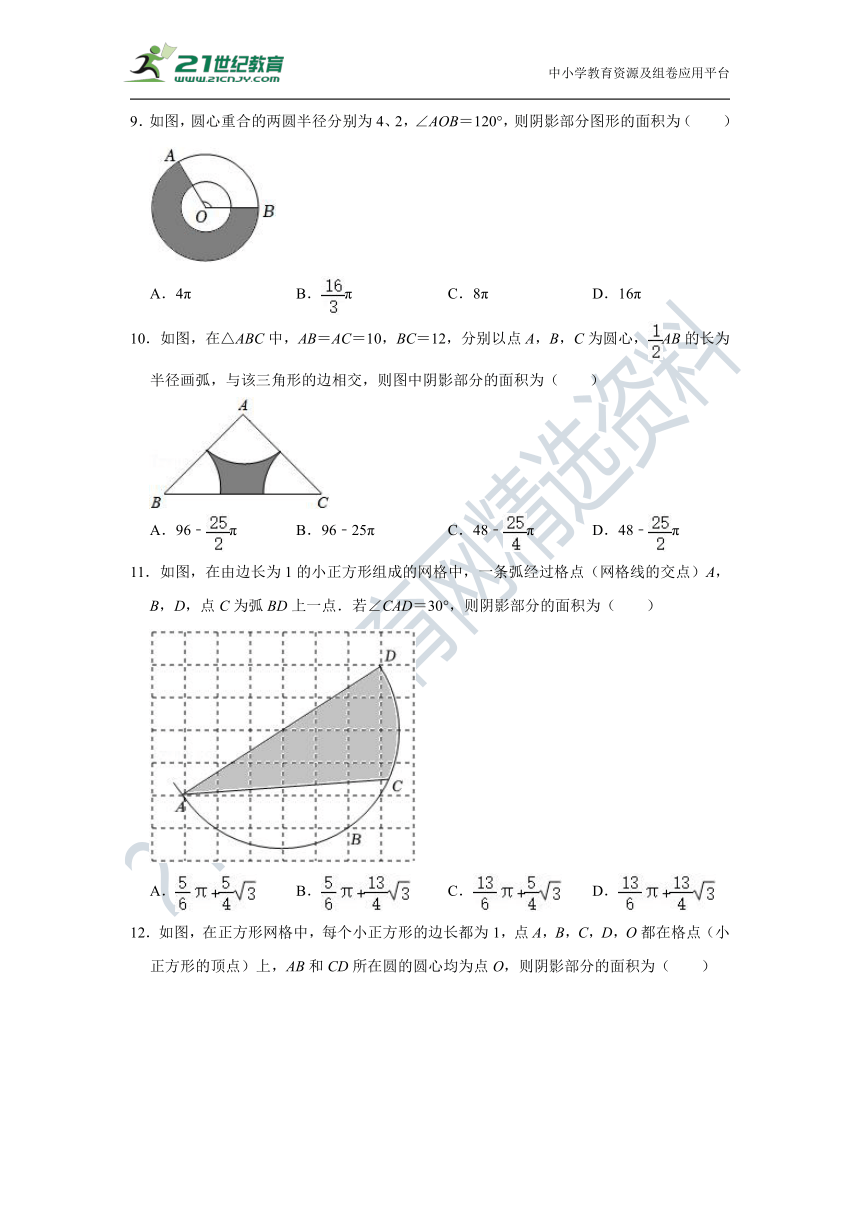
9.如图,圆心重合的两圆半径分别为4、2,∠AOB=120°,则阴影部分图形的面积为( )
A.4π B.π C.8π D.16π
10.如图,在△ABC中,AB=AC=10,BC=12,分别以点A,B,C为圆心,AB的长为半径画弧,与该三角形的边相交,则图中阴影部分的面积为( )
A.96﹣π B.96﹣25π C.48﹣π D.48﹣π
11.如图,在由边长为1的小正方形组成的网格中,一条弧经过格点(网格线的交点)A,B,D,点C为弧BD上一点.若∠CAD=30°,则阴影部分的面积为( )
A. B. C. D.
12.如图,在正方形网格中,每个小正方形的边长都为1,点A,B,C,D,O都在格点(小正方形的顶点)上,AB和CD所在圆的圆心均为点O,则阴影部分的面积为( )
A.π﹣2 B.π﹣2 C.2π D.π
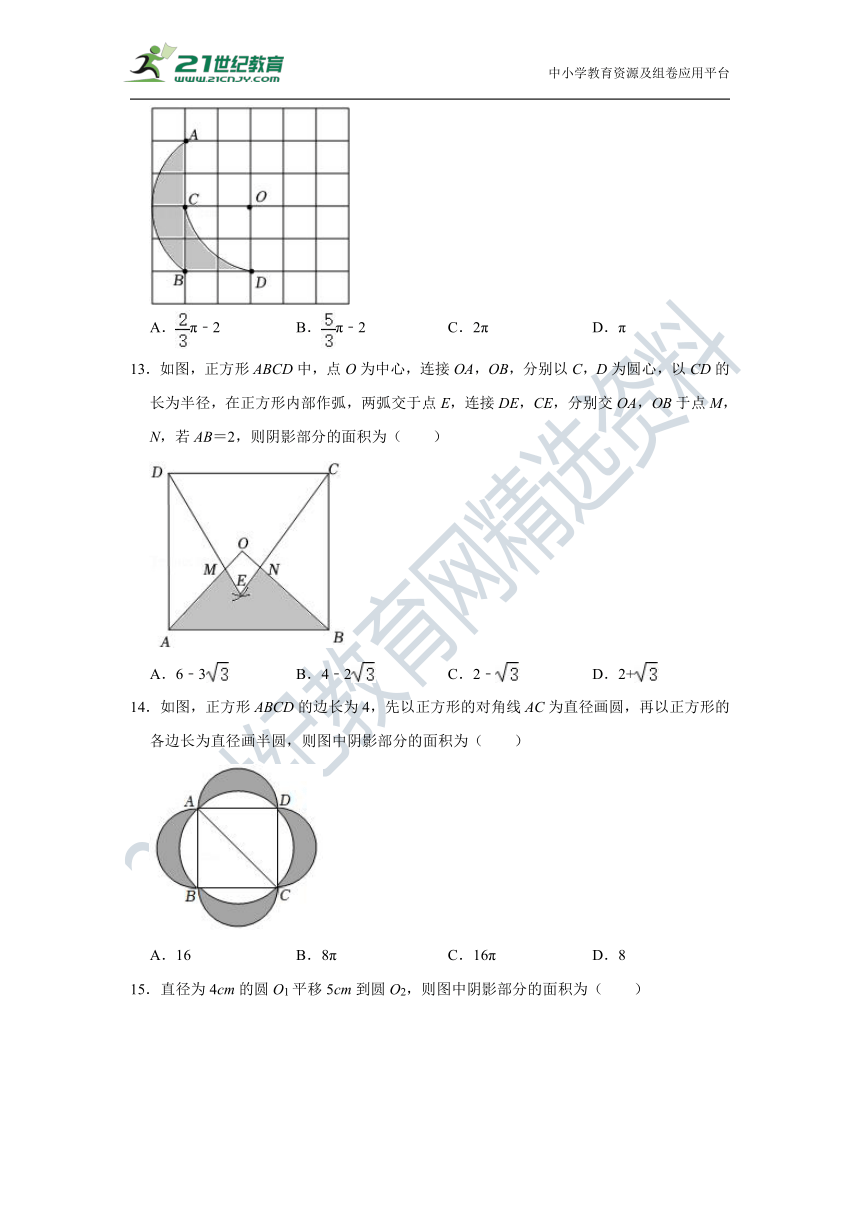
13.如图,正方形ABCD中,点O为中心,连接OA,OB,分别以C,D为圆心,以CD的长为半径,在正方形内部作弧,两弧交于点E,连接DE,CE,分别交OA,OB于点M,N,若AB=2,则阴影部分的面积为( )
A.6﹣3 B.4﹣2 C.2﹣ D.2+
14.如图,正方形ABCD的边长为4,先以正方形的对角线AC为直径画圆,再以正方形的各边长为直径画半圆,则图中阴影部分的面积为( )
A.16 B.8π C.16π D.8
15.直径为4cm的圆O1平移5cm到圆O2,则图中阴影部分的面积为( )
A.2πcm2 B.10cm2 C.4πcm2 D.20cm2
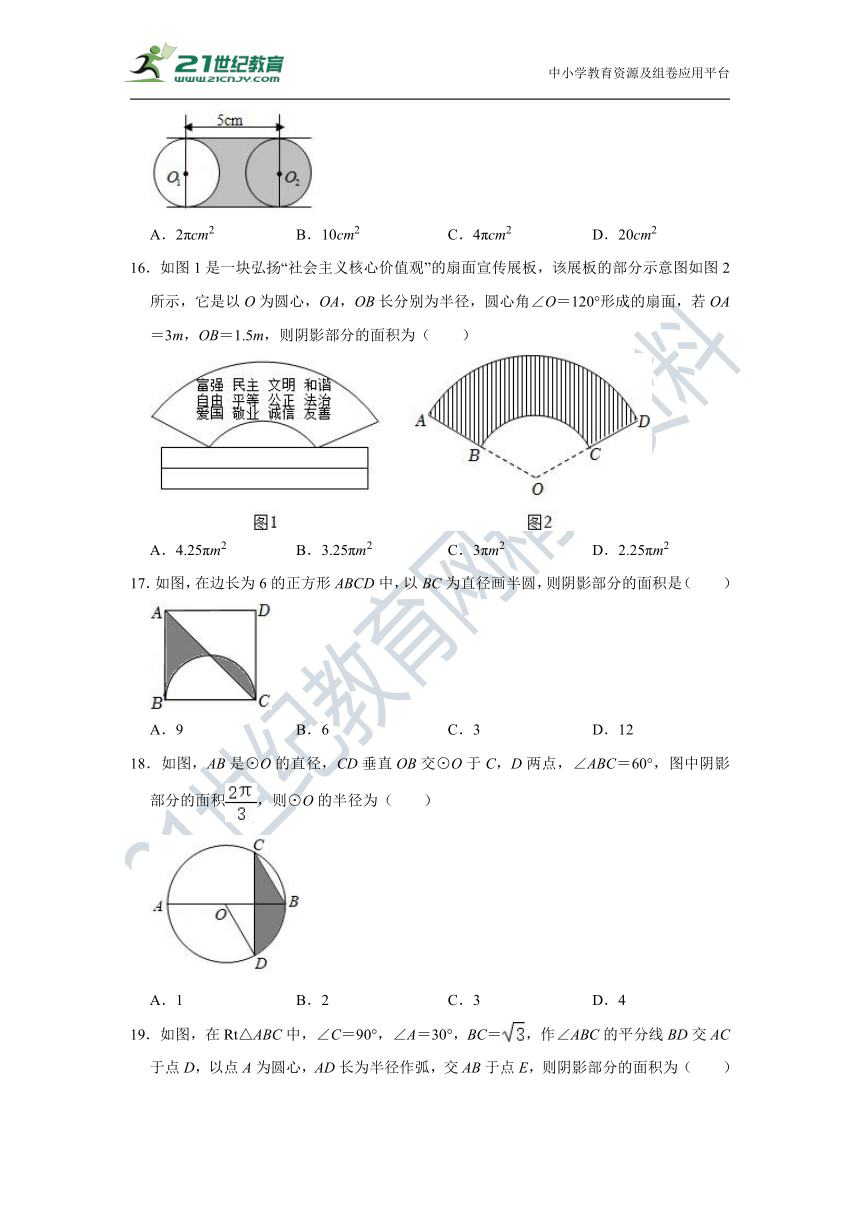
16.如图1是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以O为圆心,OA,OB长分别为半径,圆心角∠O=120°形成的扇面,若OA=3m,OB=1.5m,则阴影部分的面积为( )
A.4.25πm2 B.3.25πm2 C.3πm2 D.2.25πm2
17.如图,在边长为6的正方形ABCD中,以BC为直径画半圆,则阴影部分的面积是( )
A.9 B.6 C.3 D.12
18.如图,AB是⊙O的直径,CD垂直OB交⊙O于C,D两点,∠ABC=60°,图中阴影部分的面积,则⊙O的半径为( )
A.1 B.2 C.3 D.4
19.如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=,作∠ABC的平分线BD交AC于点D,以点A为圆心,AD长为半径作弧,交AB于点E,则阴影部分的面积为( )
A. B. C. D.
20.如图,扇形OAB中,∠AOB=120°,OA=2,点C为OB的中点,将扇形OAB绕点C顺时针旋转,点O的对应点为O',连接O'B,当O'C∥OA时,阴影部分的面积为( )
A. B. C.﹣ D.
21.如图,已知平行四边形ABCD,以B为圆心,AB为半径作交BC于E,然后以C为圆心,CE为半径作交CD于F,若AD=5,FD=3,∠B=60°,则阴影部分的面积为( )
A.π B.3π C.π D.12π
22.如图,在半圆O中,AB是半圆O的直径,AB=4,OC⊥AB,连接BC,以BC为直径作半圆,则图中阴影部分的面积为( )
A.1 B. C.2 D.π
23.如图,一件扇形艺术品完全打开后,AB,AC夹角为120°,AB的长为45cm,扇面BD的长为30cm,则扇面的面积是( )
A.375πcm2 B.450πcm2 C.600πcm2 D.750πcm2
24.一个扇形的弧长是10πcm,其圆心角是150°,此扇形的面积为( )
A.30πcm2 B.60πcm2 C.120πcm2 D.180πcm2
25.如图,AB是⊙O的直径,将弦AC绕点A顺时针旋转30°得到AD,此时点C的对应点D落在AB上,延长CD,交⊙O于点E,若CE=4,则图中阴影部分的面积为( )
A.2π B.2 C.2π﹣4 D.2π﹣2
26.如图,将Rt△CAB绕点B按逆时针方向旋转90°后,得到Rt△A′BC′,已知∠BAC=90°,∠ABC=60°,BC=2,则图中阴影部分面积为( )
A.π B.π C.π﹣ D.π
27.如图,点O是半圆圆心,BE是半圆的直径,点A,D在半圆上,且AD∥BO,∠ABO=60°,AB=8,过点D作DC⊥BE于点C,则阴影部分的面积是( )
A. B. C. D.
28.如图,在正方形ABCD中,AC和BD交于点O,过点O的直线EF交AB于点E(E不与A,B重合),交CD于点F.以点O为圆心,OC为半径的圆交直线EF于点M,N.若AB=1,则图中阴影部分的面积为( )
A.﹣ B.﹣ C.﹣ D.﹣
29.如图,AB是半圆的直径,点C在直径上,以C为圆心、CA为半径向内作直角扇形,再以D为圆心、C为半径向内作直角扇形,使点E刚好落到半圆上,若AB=10,则阴影部分的面积为( )
A.16π B.12π C.8π D.4π
30.如图,在矩形ABCD中,AB=4,AB>BC,以点A为圆心、AB长为半径的弧BE与DC相交于点E,点E为DC的中点,则由BC、CE和弧BE围成的阴影部分图形的面积是( )
A. B. C. D.
参考答案
1.把一个圆的面积按3:5剪成两个扇形,已知大扇形的面积比小扇形多104平方厘米,大扇形的面积是( )平方厘米.
A.416 B.260 C.156 D.208
解:∵把一个圆的面积按3:5剪成两个扇形,
∴设大扇形的面积为5x平方厘米,小扇形的面积为3x平方厘米,
根据题意得,5x﹣3x=104,
解得x=52,
∴5x=260,
故大扇形的面积是260平方厘米,
故选:B.
2.如图,扇形AOB圆心角为直角,OA=10,点C在上,以OA,CA为邻边构造 ACDO,边CD交OB于点E,若OE=8,则图中两块阴影部分的面积和为( )
A.10π﹣8 B.5π﹣8 C.25π﹣64 D.50π﹣64
解:连接OC.
∵四边形OACD是平行四边形,
∴OA∥CD,
∴∠OEC+∠EOA=90°,
∵∠AOB=90°,
∴∠OEC=90°,
∴EC===8,
∴S阴=S扇形AOB﹣S梯形OECA=﹣×(6+10)×8=25π﹣64.
故选:C.
3.如图,在菱形ABCD中,点E是BC的中点,以C为圆心、CE为半径作弧,交CD于点F,连接AE、AF.若AB=12,∠B=60°,则阴影部分的面积为( )
A.18﹣12π B.36﹣6π C.36﹣12π D.18﹣6π
解:如图,连接AC,
∵四边形ABCD是菱形,
∴AB=BC=12,
∵∠B=60°,E为BC的中点,
∴CE=BE=6=CF,△ABC是等边三角形,AB∥CD,
∵∠B=60°,
∴∠BCD=180°﹣∠B=120°,
由勾股定理得:AE==6,
∴S△AEB=S△AEC=×12×6×=18=S△AFC,
∴阴影部分的面积S=S△AEC+S△AFC﹣S扇形CEF=18+18﹣=36﹣12π,
故选:C.
4.如图,正方形ABCD的边长为2,O为对角线的交点,点E,F分别为BC,AD的中点.以C为圆心,BC为半径作圆弧BD,再分别以E,F为圆心,BE为半径作圆弧BO,OD,则图中阴影部分的面积为( )
A.π﹣1 B.π﹣3 C.π﹣2 D.4﹣π
解:连接BD,EF,如图,
∵正方形ABCD的边长为2,O为对角线的交点,
由题意可得:EF,BD经过点O,且EF⊥AD,EF⊥CB.
∵点E,F分别为BC,AD的中点,
∴FD=FO=EO=EB=1,
∴=,OB=OD.
∴弓形OB=弓形OD.
∴阴影部分的面积等于弓形BD的面积.
∴S阴影=S扇形CBD﹣S△CBD=﹣=π﹣2.
故选:C.
5.如图,在△ABC中,AB=AC=4,∠BAC=120°,AO是△ABC的中线.以O为圆心,OA长为半径作半圆,分别交AB,AC于点D,E,交BC于点F,G.则图中阴影部分的面积为( )
A.2﹣π B. C.4﹣π D.π
解:连接DO,过点O作OH⊥AB,垂足为H,如图,
∵AB=AC=4,∠BAC=120°,
∴=30°,
∴=2,BO===2,
∴S△ABO==2=2,
∵∠ABO=60°,
∴∠AOH=30°,
∴==1,AH===,
∴S△ADO===,
∵∠DOF=90°﹣60°=30°,DO=2,
S扇DOF===,
S阴BDF=S△ABO﹣S△ADO﹣S扇DOF=2﹣=,
S阴=2S阴BDF=2.
故选:A.
6.如图,在矩形ABCD中,AB=2,BC=,以点B为圆心,BA长为半径画弧,交CD于点E,连接BE,则扇形BAE的面积为( )
A. B. C. D.
解:∵四边形ABCD是矩形,
∴∠ABC=∠C=90°,
∵BA=BE=2,BC=,
∴cos∠CBE==,
∴∠CBE=30°,
∴∠ABE=90°﹣30°=60°,
∴S扇形BAE==,
故选:C.
7.如图,四边形ABCD为正方形,边长为4,以B为圆心、BC长为半径画,E为四边形内部一点,且BE⊥CE,∠BCE=30°,连接AE,则阴影部分面积( )
A. B.6π C. D.
解:如图,作EF⊥AB于点F,
∵BE⊥CE,∠BCE=30°,
∴BE=BC=2,∠CBE=60°,
∴CE=BE=2,∠EBF=30°,
∴EF=BE=1,
∴S阴影=S扇形ABC﹣S△BCE﹣S△ABE
=﹣×2×﹣×1
=4π﹣2﹣2.
故选:C.
8.如图,AB是⊙O的直径,弦CD⊥AB,垂足为点M.连接OC,DB.如果OC∥DB,图中阴影部分的面积是2π,那么图中阴影部分的弧长是( )
A. B. C. D.
解:连接OD,BC.
∵CD⊥AB,OC=OD,
∴DM=CM,∠COB=∠BOD,
∵OC∥BD,
∴∠COB=∠OBD,
∴∠BOD=∠OBD,
∴OD=DB,
∴△BOD是等边三角形,
∴∠BOD=60°,
∵OC∥DB,
∴S△OBD=S△CBD,
∴图中阴影部分的面积==2π,
∴OC=2或﹣2(舍去),
∴的长==π,
故选:B.
9.如图,圆心重合的两圆半径分别为4、2,∠AOB=120°,则阴影部分图形的面积为( )
A.4π B.π C.8π D.16π
解:S阴影=﹣=8π.
故选:C.
10.如图,在△ABC中,AB=AC=10,BC=12,分别以点A,B,C为圆心,AB的长为半径画弧,与该三角形的边相交,则图中阴影部分的面积为( )
A.96﹣π B.96﹣25π C.48﹣π D.48﹣π
解:作AD⊥BC于点D,
∵AB=AC=10,BC=12,
∴BD=CD=6,
∴AD==8,
∴S阴影部分=×12×8﹣π×52=48﹣.
故选:D.
11.如图,在由边长为1的小正方形组成的网格中,一条弧经过格点(网格线的交点)A,B,D,点C为弧BD上一点.若∠CAD=30°,则阴影部分的面积为( )
A. B. C. D.
解:如图,连接AB,BD,OC,CD.
∵AB=BD=,AD=2,
∴AB2+BD2=AD2,
∴∠ABD=90°,
∴AD是⊙O的直径,
∴OA=OD=OC=,
∴∠ACD=90°,
∵∠DAC=30°,
∴∠DOC=60°,
∴CD=AD=,AC=CD=,
∴S阴=S△AOC+S扇形DOC
=×××+
=+,
故选:D.
12.如图,在正方形网格中,每个小正方形的边长都为1,点A,B,C,D,O都在格点(小正方形的顶点)上,AB和CD所在圆的圆心均为点O,则阴影部分的面积为( )
A.π﹣2 B.π﹣2 C.2π D.π
解:如图,连接,OA,OB,OD.
S阴=S扇形AOB+S△OBD﹣S△AOC﹣S扇形OCD
=S扇形AOB﹣S扇形COD
=﹣
=π,
故选:D.
13.如图,正方形ABCD中,点O为中心,连接OA,OB,分别以C,D为圆心,以CD的长为半径,在正方形内部作弧,两弧交于点E,连接DE,CE,分别交OA,OB于点M,N,若AB=2,则阴影部分的面积为( )
A.6﹣3 B.4﹣2 C.2﹣ D.2+
解:如图,连接MN,连接EO并延长交CD于点F,则EF⊥CD,
由尺规作图可知ED=EC=CD=2,
∴EF=,
∵OF=1,
∴OE=﹣1,
∵OE∥AD,
∴=,
即=,
∴OM=2﹣,
∴MN=OM=4﹣2,
∴S四边形OMEN=OE MN=×()×(4﹣2)=3﹣5,
∴阴影部分的面积为1﹣(3﹣5)=6﹣3.
故选:A.
14.如图,正方形ABCD的边长为4,先以正方形的对角线AC为直径画圆,再以正方形的各边长为直径画半圆,则图中阴影部分的面积为( )
A.16 B.8π C.16π D.8
解:∵正方形ABCD的边长为4,
∴AC=4,
∴图中阴影部分的面积=S正方形ABCD+4×以正方形的各边长为直径的半圆的面积﹣以正方形的对角线AC为直径圆的面积
=4×4+4××22π﹣(2)2π=16,
故选:A.
15.直径为4cm的圆O1平移5cm到圆O2,则图中阴影部分的面积为( )
A.2πcm2 B.10cm2 C.4πcm2 D.20cm2
解:如图,
阴影部分的面积=矩形ABCD的面积=4×5=20,
故选:D.
16.如图1是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以O为圆心,OA,OB长分别为半径,圆心角∠O=120°形成的扇面,若OA=3m,OB=1.5m,则阴影部分的面积为( )
A.4.25πm2 B.3.25πm2 C.3πm2 D.2.25πm2
解:S阴=S扇形DOA﹣S扇形BOC
=﹣
=2.25πm2.
故选:D.
17.如图,在边长为6的正方形ABCD中,以BC为直径画半圆,则阴影部分的面积是( )
A.9 B.6 C.3 D.12
解:设AC与半圆交于点E,半圆的圆心为O,连接BE,OE,
∵四边形ABCD是正方形,
∴∠OCE=45°,
∵OE=OC,
∴∠OEC=∠OCE=45°,
∴∠EOC=90°,
∴OE垂直平分BC,
∴BE=CE,
∴弓形BE的面积=弓形CE的面积,
∴,
故选:A.
18.如图,AB是⊙O的直径,CD垂直OB交⊙O于C,D两点,∠ABC=60°,图中阴影部分的面积,则⊙O的半径为( )
A.1 B.2 C.3 D.4
解:如图,连接AC,
∵AB是⊙O的直径,
∴∠ACB=90°,
又∵∠ABC=60°,
∴∠BAC=90°﹣60°=30°,
∴∠BOD=2∠BAC=60°,
设⊙O的半径为R,
由于S阴影部分=S扇形BOD=,
所以=,
所以R=2,
故选:B.
19.如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=,作∠ABC的平分线BD交AC于点D,以点A为圆心,AD长为半径作弧,交AB于点E,则阴影部分的面积为( )
A. B. C. D.
解:在Rt△ABC中,∠C=90°,∠A=30°,BC=,
∴AC=BC=3,∠ABC=90°﹣30°=60°,
∵BD是∠ABC的平分线,
∴∠CBD=30°,
在Rt△BCD中,CD=BC tan30°=1,
∴AD=3﹣1=2,
∴S阴影部分=S扇形ADE
=
=,
故选:A.
20.如图,扇形OAB中,∠AOB=120°,OA=2,点C为OB的中点,将扇形OAB绕点C顺时针旋转,点O的对应点为O',连接O'B,当O'C∥OA时,阴影部分的面积为( )
A. B. C.﹣ D.
解:连接OO′,
∵O'C∥OA,∠AOB=120°,
∴∠OCO′=60°,
∵C是OB的中点,
∴OC=CB=CO′=1,
∴△OCO′是等边三角形,
∴∠OO′C=∠COO′=60°,∠CBO′=∠CO′B=30°,
∴∠OO′B=∠A′O′B=90°,
∴O,O′,A′三点共线,BO′=,
阴影部分的面积为S扇形BOD﹣S△OBO′=﹣
=﹣.
故选:D.
21.如图,已知平行四边形ABCD,以B为圆心,AB为半径作交BC于E,然后以C为圆心,CE为半径作交CD于F,若AD=5,FD=3,∠B=60°,则阴影部分的面积为( )
A.π B.3π C.π D.12π
解:设BE=a,CE=b,
根据题意可得,
,
解得:,
∴BE=4,CE=1,
∵四边形ABCD是平行四边形,
∴∠B+∠C=180°,
∴∠C=180°﹣∠B=180°﹣60°=120°,
∴S扇ABE===,
S扇ECF===,
S阴=S扇ABE+S扇ECF=3π.
故选:B.
22.如图,在半圆O中,AB是半圆O的直径,AB=4,OC⊥AB,连接BC,以BC为直径作半圆,则图中阴影部分的面积为( )
A.1 B. C.2 D.π
解:根据题意可得,
∵OB=OC=2,
∴BC==2,
∴以BC为直径半圆的面积S1=×()2=π,
∴扇形BOC的面积S2==π,
∴△BOC的面积S3===2,
∴则弓形BC的面积S4=S2﹣S3=π﹣2,
∴则阴影部分的面积为S阴=S1﹣S4=π﹣(π﹣2)=2.
故选:C.
23.如图,一件扇形艺术品完全打开后,AB,AC夹角为120°,AB的长为45cm,扇面BD的长为30cm,则扇面的面积是( )
A.375πcm2 B.450πcm2 C.600πcm2 D.750πcm2
解:∵AB的长是45cm,扇面BD的长为30cm,
∴AD=AB﹣BD=15cm,
∵∠BAC=120°,
∴扇面的面积S=S扇形BAC﹣S扇形DAE
=﹣
=600π(cm2),
故选:C.
24.一个扇形的弧长是10πcm,其圆心角是150°,此扇形的面积为( )
A.30πcm2 B.60πcm2 C.120πcm2 D.180πcm2
解:根据题意可得,
设扇形的半径为rcm,
则l=,
即10π=,
解得:r=12,
∴S===60π(cm2).
故选:B.
25.如图,AB是⊙O的直径,将弦AC绕点A顺时针旋转30°得到AD,此时点C的对应点D落在AB上,延长CD,交⊙O于点E,若CE=4,则图中阴影部分的面积为( )
A.2π B.2 C.2π﹣4 D.2π﹣2
解:连接OE,OC,BC,
由旋转知AC=AD,∠CAD=30°,
∴∠BOC=60°,∠ACE=(180°﹣30°)÷2=75°,
∴∠BCE=90°﹣∠ACE=15°,
∴∠BOE=2∠BCE=30°,
∴∠EOC=90°,
即△EOC为等腰直角三角形,
∵CE=4,
∴OE=OC=2,
∴S阴影=S扇形OEC﹣S△OEC=﹣×=2π﹣4,
故选:C.
26.如图,将Rt△CAB绕点B按逆时针方向旋转90°后,得到Rt△A′BC′,已知∠BAC=90°,∠ABC=60°,BC=2,则图中阴影部分面积为( )
A.π B.π C.π﹣ D.π
解:根据题意可得,
∠CBC′=90°,
S扇CBC′===π,
∵BC=2,∠BAC=60°,
∴AC==1,AB=,
∴=,
∵∠CBA′=90°﹣∠ABC=90°﹣60°=30°,
∴S扇DBA′===,
∴S阴=S扇CBC′﹣S△A′BC′﹣S扇DBA′==.
故选:C.
27.如图,点O是半圆圆心,BE是半圆的直径,点A,D在半圆上,且AD∥BO,∠ABO=60°,AB=8,过点D作DC⊥BE于点C,则阴影部分的面积是( )
A. B. C. D.
解:连接OA,
∵∠ABO=60°,OA=OB,
∴△AOB是等边三角形,
∵AB=8,∠AOB=60°,
∴⊙O的半径为8,∠AOE=120°,
∵AD∥OB,
∴∠OAD=∠AOB=60°,
∵OA=OD,
∴∠AOD=60°,
∵∠AOB=∠AOD=60°,
∴∠DOE=60°,
∵DC⊥BE于点C,
∴CD=OD=4,OC=OD=4,
∴BC=8+4=12,
∴S阴影=S△AOB+S扇形OAE﹣S△BCD
=×8×4+﹣×12×4
=﹣8,
故选:A.
28.如图,在正方形ABCD中,AC和BD交于点O,过点O的直线EF交AB于点E(E不与A,B重合),交CD于点F.以点O为圆心,OC为半径的圆交直线EF于点M,N.若AB=1,则图中阴影部分的面积为( )
A.﹣ B.﹣ C.﹣ D.﹣
解:以OD为半径作弧DN,
∵四边形ABCD是正方形,
∴OB=OD=OC,∠DOC=90°,
∵∠EOB=∠FOD,
∴S扇形BOM=S扇形DON,
∴S阴影=S扇形DOC﹣S△DOC=﹣×1×1=﹣,
故选:B.
29.如图,AB是半圆的直径,点C在直径上,以C为圆心、CA为半径向内作直角扇形,再以D为圆心、C为半径向内作直角扇形,使点E刚好落到半圆上,若AB=10,则阴影部分的面积为( )
A.16π B.12π C.8π D.4π
解:如图,过点E作EF⊥AB于点F,连接AE、BE,
∵AB是半圆的直径,
∴∠AEB=90°,即∠EAB+∠EBA=90°,
∵EF⊥AB,
∴∠AFE=∠EFB=90°,
∴∠EAB+∠AEF=90°,
∴∠EBA=∠AEF,
∴△AEF∽△EBF,
∴,即EF2=AF BF,
设AC=x,
∵EF⊥AB,且由作图可知阴影部分是两个半径相等的半圆,
∴四边形DCFE是正方形,
∴CD=DE=EF=CF=AC=x,
∴AF=2x,
∴BF=10﹣2x,
∴x2=2x(10﹣2x),
∴x1=0(舍),x2=4,
∴S阴影=2×=8π.
故选:C.
30.如图,在矩形ABCD中,AB=4,AB>BC,以点A为圆心、AB长为半径的弧BE与DC相交于点E,点E为DC的中点,则由BC、CE和弧BE围成的阴影部分图形的面积是( )
A. B. C. D.
解:由题意可得:AB=AE=CD=4,∠D=∠DAB=90°,
∵点E是DC的中点,
∴DE=2=,
∴∠DAE=30°,AD==,
∴∠EAB=∠DAB﹣∠DAE=90°﹣30°=60°,
∴S阴影=S矩形ABCD﹣SRt△ADE﹣S扇形ABE
=4×﹣﹣
=.
故选:A.
扇形面积计算选择题专项练习
1.把一个圆的面积按3:5剪成两个扇形,已知大扇形的面积比小扇形多104平方厘米,大扇形的面积是( )平方厘米.
A.416 B.260 C.156 D.208
2.如图,扇形AOB圆心角为直角,OA=10,点C在上,以OA,CA为邻边构造 ACDO,边CD交OB于点E,若OE=8,则图中两块阴影部分的面积和为( )
A.10π﹣8 B.5π﹣8 C.25π﹣64 D.50π﹣64
3.如图,在菱形ABCD中,点E是BC的中点,以C为圆心、CE为半径作弧,交CD于点F,连接AE、AF.若AB=12,∠B=60°,则阴影部分的面积为( )
A.18﹣12π B.36﹣6π C.36﹣12π D.18﹣6π
4.如图,正方形ABCD的边长为2,O为对角线的交点,点E,F分别为BC,AD的中点.以C为圆心,BC为半径作圆弧BD,再分别以E,F为圆心,BE为半径作圆弧BO,OD,则图中阴影部分的面积为( )
A.π﹣1 B.π﹣3 C.π﹣2 D.4﹣π
5.如图,在△ABC中,AB=AC=4,∠BAC=120°,AO是△ABC的中线.以O为圆心,OA长为半径作半圆,分别交AB,AC于点D,E,交BC于点F,G.则图中阴影部分的面积为( )
A.2﹣π B. C.4﹣π D.π
6.如图,在矩形ABCD中,AB=2,BC=,以点B为圆心,BA长为半径画弧,交CD于点E,连接BE,则扇形BAE的面积为( )
A. B. C. D.
7.如图,四边形ABCD为正方形,边长为4,以B为圆心、BC长为半径画,E为四边形内部一点,且BE⊥CE,∠BCE=30°,连接AE,则阴影部分面积( )
A. B.6π C. D.
8.如图,AB是⊙O的直径,弦CD⊥AB,垂足为点M.连接OC,DB.如果OC∥DB,图中阴影部分的面积是2π,那么图中阴影部分的弧长是( )
A. B. C. D.
9.如图,圆心重合的两圆半径分别为4、2,∠AOB=120°,则阴影部分图形的面积为( )
A.4π B.π C.8π D.16π
10.如图,在△ABC中,AB=AC=10,BC=12,分别以点A,B,C为圆心,AB的长为半径画弧,与该三角形的边相交,则图中阴影部分的面积为( )
A.96﹣π B.96﹣25π C.48﹣π D.48﹣π
11.如图,在由边长为1的小正方形组成的网格中,一条弧经过格点(网格线的交点)A,B,D,点C为弧BD上一点.若∠CAD=30°,则阴影部分的面积为( )
A. B. C. D.
12.如图,在正方形网格中,每个小正方形的边长都为1,点A,B,C,D,O都在格点(小正方形的顶点)上,AB和CD所在圆的圆心均为点O,则阴影部分的面积为( )
A.π﹣2 B.π﹣2 C.2π D.π
13.如图,正方形ABCD中,点O为中心,连接OA,OB,分别以C,D为圆心,以CD的长为半径,在正方形内部作弧,两弧交于点E,连接DE,CE,分别交OA,OB于点M,N,若AB=2,则阴影部分的面积为( )
A.6﹣3 B.4﹣2 C.2﹣ D.2+
14.如图,正方形ABCD的边长为4,先以正方形的对角线AC为直径画圆,再以正方形的各边长为直径画半圆,则图中阴影部分的面积为( )
A.16 B.8π C.16π D.8
15.直径为4cm的圆O1平移5cm到圆O2,则图中阴影部分的面积为( )
A.2πcm2 B.10cm2 C.4πcm2 D.20cm2
16.如图1是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以O为圆心,OA,OB长分别为半径,圆心角∠O=120°形成的扇面,若OA=3m,OB=1.5m,则阴影部分的面积为( )
A.4.25πm2 B.3.25πm2 C.3πm2 D.2.25πm2
17.如图,在边长为6的正方形ABCD中,以BC为直径画半圆,则阴影部分的面积是( )
A.9 B.6 C.3 D.12
18.如图,AB是⊙O的直径,CD垂直OB交⊙O于C,D两点,∠ABC=60°,图中阴影部分的面积,则⊙O的半径为( )
A.1 B.2 C.3 D.4
19.如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=,作∠ABC的平分线BD交AC于点D,以点A为圆心,AD长为半径作弧,交AB于点E,则阴影部分的面积为( )
A. B. C. D.
20.如图,扇形OAB中,∠AOB=120°,OA=2,点C为OB的中点,将扇形OAB绕点C顺时针旋转,点O的对应点为O',连接O'B,当O'C∥OA时,阴影部分的面积为( )
A. B. C.﹣ D.
21.如图,已知平行四边形ABCD,以B为圆心,AB为半径作交BC于E,然后以C为圆心,CE为半径作交CD于F,若AD=5,FD=3,∠B=60°,则阴影部分的面积为( )
A.π B.3π C.π D.12π
22.如图,在半圆O中,AB是半圆O的直径,AB=4,OC⊥AB,连接BC,以BC为直径作半圆,则图中阴影部分的面积为( )
A.1 B. C.2 D.π
23.如图,一件扇形艺术品完全打开后,AB,AC夹角为120°,AB的长为45cm,扇面BD的长为30cm,则扇面的面积是( )
A.375πcm2 B.450πcm2 C.600πcm2 D.750πcm2
24.一个扇形的弧长是10πcm,其圆心角是150°,此扇形的面积为( )
A.30πcm2 B.60πcm2 C.120πcm2 D.180πcm2
25.如图,AB是⊙O的直径,将弦AC绕点A顺时针旋转30°得到AD,此时点C的对应点D落在AB上,延长CD,交⊙O于点E,若CE=4,则图中阴影部分的面积为( )
A.2π B.2 C.2π﹣4 D.2π﹣2
26.如图,将Rt△CAB绕点B按逆时针方向旋转90°后,得到Rt△A′BC′,已知∠BAC=90°,∠ABC=60°,BC=2,则图中阴影部分面积为( )
A.π B.π C.π﹣ D.π
27.如图,点O是半圆圆心,BE是半圆的直径,点A,D在半圆上,且AD∥BO,∠ABO=60°,AB=8,过点D作DC⊥BE于点C,则阴影部分的面积是( )
A. B. C. D.
28.如图,在正方形ABCD中,AC和BD交于点O,过点O的直线EF交AB于点E(E不与A,B重合),交CD于点F.以点O为圆心,OC为半径的圆交直线EF于点M,N.若AB=1,则图中阴影部分的面积为( )
A.﹣ B.﹣ C.﹣ D.﹣
29.如图,AB是半圆的直径,点C在直径上,以C为圆心、CA为半径向内作直角扇形,再以D为圆心、C为半径向内作直角扇形,使点E刚好落到半圆上,若AB=10,则阴影部分的面积为( )
A.16π B.12π C.8π D.4π
30.如图,在矩形ABCD中,AB=4,AB>BC,以点A为圆心、AB长为半径的弧BE与DC相交于点E,点E为DC的中点,则由BC、CE和弧BE围成的阴影部分图形的面积是( )
A. B. C. D.
参考答案
1.把一个圆的面积按3:5剪成两个扇形,已知大扇形的面积比小扇形多104平方厘米,大扇形的面积是( )平方厘米.
A.416 B.260 C.156 D.208
解:∵把一个圆的面积按3:5剪成两个扇形,
∴设大扇形的面积为5x平方厘米,小扇形的面积为3x平方厘米,
根据题意得,5x﹣3x=104,
解得x=52,
∴5x=260,
故大扇形的面积是260平方厘米,
故选:B.
2.如图,扇形AOB圆心角为直角,OA=10,点C在上,以OA,CA为邻边构造 ACDO,边CD交OB于点E,若OE=8,则图中两块阴影部分的面积和为( )
A.10π﹣8 B.5π﹣8 C.25π﹣64 D.50π﹣64
解:连接OC.
∵四边形OACD是平行四边形,
∴OA∥CD,
∴∠OEC+∠EOA=90°,
∵∠AOB=90°,
∴∠OEC=90°,
∴EC===8,
∴S阴=S扇形AOB﹣S梯形OECA=﹣×(6+10)×8=25π﹣64.
故选:C.
3.如图,在菱形ABCD中,点E是BC的中点,以C为圆心、CE为半径作弧,交CD于点F,连接AE、AF.若AB=12,∠B=60°,则阴影部分的面积为( )
A.18﹣12π B.36﹣6π C.36﹣12π D.18﹣6π
解:如图,连接AC,
∵四边形ABCD是菱形,
∴AB=BC=12,
∵∠B=60°,E为BC的中点,
∴CE=BE=6=CF,△ABC是等边三角形,AB∥CD,
∵∠B=60°,
∴∠BCD=180°﹣∠B=120°,
由勾股定理得:AE==6,
∴S△AEB=S△AEC=×12×6×=18=S△AFC,
∴阴影部分的面积S=S△AEC+S△AFC﹣S扇形CEF=18+18﹣=36﹣12π,
故选:C.
4.如图,正方形ABCD的边长为2,O为对角线的交点,点E,F分别为BC,AD的中点.以C为圆心,BC为半径作圆弧BD,再分别以E,F为圆心,BE为半径作圆弧BO,OD,则图中阴影部分的面积为( )
A.π﹣1 B.π﹣3 C.π﹣2 D.4﹣π
解:连接BD,EF,如图,
∵正方形ABCD的边长为2,O为对角线的交点,
由题意可得:EF,BD经过点O,且EF⊥AD,EF⊥CB.
∵点E,F分别为BC,AD的中点,
∴FD=FO=EO=EB=1,
∴=,OB=OD.
∴弓形OB=弓形OD.
∴阴影部分的面积等于弓形BD的面积.
∴S阴影=S扇形CBD﹣S△CBD=﹣=π﹣2.
故选:C.
5.如图,在△ABC中,AB=AC=4,∠BAC=120°,AO是△ABC的中线.以O为圆心,OA长为半径作半圆,分别交AB,AC于点D,E,交BC于点F,G.则图中阴影部分的面积为( )
A.2﹣π B. C.4﹣π D.π
解:连接DO,过点O作OH⊥AB,垂足为H,如图,
∵AB=AC=4,∠BAC=120°,
∴=30°,
∴=2,BO===2,
∴S△ABO==2=2,
∵∠ABO=60°,
∴∠AOH=30°,
∴==1,AH===,
∴S△ADO===,
∵∠DOF=90°﹣60°=30°,DO=2,
S扇DOF===,
S阴BDF=S△ABO﹣S△ADO﹣S扇DOF=2﹣=,
S阴=2S阴BDF=2.
故选:A.
6.如图,在矩形ABCD中,AB=2,BC=,以点B为圆心,BA长为半径画弧,交CD于点E,连接BE,则扇形BAE的面积为( )
A. B. C. D.
解:∵四边形ABCD是矩形,
∴∠ABC=∠C=90°,
∵BA=BE=2,BC=,
∴cos∠CBE==,
∴∠CBE=30°,
∴∠ABE=90°﹣30°=60°,
∴S扇形BAE==,
故选:C.
7.如图,四边形ABCD为正方形,边长为4,以B为圆心、BC长为半径画,E为四边形内部一点,且BE⊥CE,∠BCE=30°,连接AE,则阴影部分面积( )
A. B.6π C. D.
解:如图,作EF⊥AB于点F,
∵BE⊥CE,∠BCE=30°,
∴BE=BC=2,∠CBE=60°,
∴CE=BE=2,∠EBF=30°,
∴EF=BE=1,
∴S阴影=S扇形ABC﹣S△BCE﹣S△ABE
=﹣×2×﹣×1
=4π﹣2﹣2.
故选:C.
8.如图,AB是⊙O的直径,弦CD⊥AB,垂足为点M.连接OC,DB.如果OC∥DB,图中阴影部分的面积是2π,那么图中阴影部分的弧长是( )
A. B. C. D.
解:连接OD,BC.
∵CD⊥AB,OC=OD,
∴DM=CM,∠COB=∠BOD,
∵OC∥BD,
∴∠COB=∠OBD,
∴∠BOD=∠OBD,
∴OD=DB,
∴△BOD是等边三角形,
∴∠BOD=60°,
∵OC∥DB,
∴S△OBD=S△CBD,
∴图中阴影部分的面积==2π,
∴OC=2或﹣2(舍去),
∴的长==π,
故选:B.
9.如图,圆心重合的两圆半径分别为4、2,∠AOB=120°,则阴影部分图形的面积为( )
A.4π B.π C.8π D.16π
解:S阴影=﹣=8π.
故选:C.
10.如图,在△ABC中,AB=AC=10,BC=12,分别以点A,B,C为圆心,AB的长为半径画弧,与该三角形的边相交,则图中阴影部分的面积为( )
A.96﹣π B.96﹣25π C.48﹣π D.48﹣π
解:作AD⊥BC于点D,
∵AB=AC=10,BC=12,
∴BD=CD=6,
∴AD==8,
∴S阴影部分=×12×8﹣π×52=48﹣.
故选:D.
11.如图,在由边长为1的小正方形组成的网格中,一条弧经过格点(网格线的交点)A,B,D,点C为弧BD上一点.若∠CAD=30°,则阴影部分的面积为( )
A. B. C. D.
解:如图,连接AB,BD,OC,CD.
∵AB=BD=,AD=2,
∴AB2+BD2=AD2,
∴∠ABD=90°,
∴AD是⊙O的直径,
∴OA=OD=OC=,
∴∠ACD=90°,
∵∠DAC=30°,
∴∠DOC=60°,
∴CD=AD=,AC=CD=,
∴S阴=S△AOC+S扇形DOC
=×××+
=+,
故选:D.
12.如图,在正方形网格中,每个小正方形的边长都为1,点A,B,C,D,O都在格点(小正方形的顶点)上,AB和CD所在圆的圆心均为点O,则阴影部分的面积为( )
A.π﹣2 B.π﹣2 C.2π D.π
解:如图,连接,OA,OB,OD.
S阴=S扇形AOB+S△OBD﹣S△AOC﹣S扇形OCD
=S扇形AOB﹣S扇形COD
=﹣
=π,
故选:D.
13.如图,正方形ABCD中,点O为中心,连接OA,OB,分别以C,D为圆心,以CD的长为半径,在正方形内部作弧,两弧交于点E,连接DE,CE,分别交OA,OB于点M,N,若AB=2,则阴影部分的面积为( )
A.6﹣3 B.4﹣2 C.2﹣ D.2+
解:如图,连接MN,连接EO并延长交CD于点F,则EF⊥CD,
由尺规作图可知ED=EC=CD=2,
∴EF=,
∵OF=1,
∴OE=﹣1,
∵OE∥AD,
∴=,
即=,
∴OM=2﹣,
∴MN=OM=4﹣2,
∴S四边形OMEN=OE MN=×()×(4﹣2)=3﹣5,
∴阴影部分的面积为1﹣(3﹣5)=6﹣3.
故选:A.
14.如图,正方形ABCD的边长为4,先以正方形的对角线AC为直径画圆,再以正方形的各边长为直径画半圆,则图中阴影部分的面积为( )
A.16 B.8π C.16π D.8
解:∵正方形ABCD的边长为4,
∴AC=4,
∴图中阴影部分的面积=S正方形ABCD+4×以正方形的各边长为直径的半圆的面积﹣以正方形的对角线AC为直径圆的面积
=4×4+4××22π﹣(2)2π=16,
故选:A.
15.直径为4cm的圆O1平移5cm到圆O2,则图中阴影部分的面积为( )
A.2πcm2 B.10cm2 C.4πcm2 D.20cm2
解:如图,
阴影部分的面积=矩形ABCD的面积=4×5=20,
故选:D.
16.如图1是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以O为圆心,OA,OB长分别为半径,圆心角∠O=120°形成的扇面,若OA=3m,OB=1.5m,则阴影部分的面积为( )
A.4.25πm2 B.3.25πm2 C.3πm2 D.2.25πm2
解:S阴=S扇形DOA﹣S扇形BOC
=﹣
=2.25πm2.
故选:D.
17.如图,在边长为6的正方形ABCD中,以BC为直径画半圆,则阴影部分的面积是( )
A.9 B.6 C.3 D.12
解:设AC与半圆交于点E,半圆的圆心为O,连接BE,OE,
∵四边形ABCD是正方形,
∴∠OCE=45°,
∵OE=OC,
∴∠OEC=∠OCE=45°,
∴∠EOC=90°,
∴OE垂直平分BC,
∴BE=CE,
∴弓形BE的面积=弓形CE的面积,
∴,
故选:A.
18.如图,AB是⊙O的直径,CD垂直OB交⊙O于C,D两点,∠ABC=60°,图中阴影部分的面积,则⊙O的半径为( )
A.1 B.2 C.3 D.4
解:如图,连接AC,
∵AB是⊙O的直径,
∴∠ACB=90°,
又∵∠ABC=60°,
∴∠BAC=90°﹣60°=30°,
∴∠BOD=2∠BAC=60°,
设⊙O的半径为R,
由于S阴影部分=S扇形BOD=,
所以=,
所以R=2,
故选:B.
19.如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=,作∠ABC的平分线BD交AC于点D,以点A为圆心,AD长为半径作弧,交AB于点E,则阴影部分的面积为( )
A. B. C. D.
解:在Rt△ABC中,∠C=90°,∠A=30°,BC=,
∴AC=BC=3,∠ABC=90°﹣30°=60°,
∵BD是∠ABC的平分线,
∴∠CBD=30°,
在Rt△BCD中,CD=BC tan30°=1,
∴AD=3﹣1=2,
∴S阴影部分=S扇形ADE
=
=,
故选:A.
20.如图,扇形OAB中,∠AOB=120°,OA=2,点C为OB的中点,将扇形OAB绕点C顺时针旋转,点O的对应点为O',连接O'B,当O'C∥OA时,阴影部分的面积为( )
A. B. C.﹣ D.
解:连接OO′,
∵O'C∥OA,∠AOB=120°,
∴∠OCO′=60°,
∵C是OB的中点,
∴OC=CB=CO′=1,
∴△OCO′是等边三角形,
∴∠OO′C=∠COO′=60°,∠CBO′=∠CO′B=30°,
∴∠OO′B=∠A′O′B=90°,
∴O,O′,A′三点共线,BO′=,
阴影部分的面积为S扇形BOD﹣S△OBO′=﹣
=﹣.
故选:D.
21.如图,已知平行四边形ABCD,以B为圆心,AB为半径作交BC于E,然后以C为圆心,CE为半径作交CD于F,若AD=5,FD=3,∠B=60°,则阴影部分的面积为( )
A.π B.3π C.π D.12π
解:设BE=a,CE=b,
根据题意可得,
,
解得:,
∴BE=4,CE=1,
∵四边形ABCD是平行四边形,
∴∠B+∠C=180°,
∴∠C=180°﹣∠B=180°﹣60°=120°,
∴S扇ABE===,
S扇ECF===,
S阴=S扇ABE+S扇ECF=3π.
故选:B.
22.如图,在半圆O中,AB是半圆O的直径,AB=4,OC⊥AB,连接BC,以BC为直径作半圆,则图中阴影部分的面积为( )
A.1 B. C.2 D.π
解:根据题意可得,
∵OB=OC=2,
∴BC==2,
∴以BC为直径半圆的面积S1=×()2=π,
∴扇形BOC的面积S2==π,
∴△BOC的面积S3===2,
∴则弓形BC的面积S4=S2﹣S3=π﹣2,
∴则阴影部分的面积为S阴=S1﹣S4=π﹣(π﹣2)=2.
故选:C.
23.如图,一件扇形艺术品完全打开后,AB,AC夹角为120°,AB的长为45cm,扇面BD的长为30cm,则扇面的面积是( )
A.375πcm2 B.450πcm2 C.600πcm2 D.750πcm2
解:∵AB的长是45cm,扇面BD的长为30cm,
∴AD=AB﹣BD=15cm,
∵∠BAC=120°,
∴扇面的面积S=S扇形BAC﹣S扇形DAE
=﹣
=600π(cm2),
故选:C.
24.一个扇形的弧长是10πcm,其圆心角是150°,此扇形的面积为( )
A.30πcm2 B.60πcm2 C.120πcm2 D.180πcm2
解:根据题意可得,
设扇形的半径为rcm,
则l=,
即10π=,
解得:r=12,
∴S===60π(cm2).
故选:B.
25.如图,AB是⊙O的直径,将弦AC绕点A顺时针旋转30°得到AD,此时点C的对应点D落在AB上,延长CD,交⊙O于点E,若CE=4,则图中阴影部分的面积为( )
A.2π B.2 C.2π﹣4 D.2π﹣2
解:连接OE,OC,BC,
由旋转知AC=AD,∠CAD=30°,
∴∠BOC=60°,∠ACE=(180°﹣30°)÷2=75°,
∴∠BCE=90°﹣∠ACE=15°,
∴∠BOE=2∠BCE=30°,
∴∠EOC=90°,
即△EOC为等腰直角三角形,
∵CE=4,
∴OE=OC=2,
∴S阴影=S扇形OEC﹣S△OEC=﹣×=2π﹣4,
故选:C.
26.如图,将Rt△CAB绕点B按逆时针方向旋转90°后,得到Rt△A′BC′,已知∠BAC=90°,∠ABC=60°,BC=2,则图中阴影部分面积为( )
A.π B.π C.π﹣ D.π
解:根据题意可得,
∠CBC′=90°,
S扇CBC′===π,
∵BC=2,∠BAC=60°,
∴AC==1,AB=,
∴=,
∵∠CBA′=90°﹣∠ABC=90°﹣60°=30°,
∴S扇DBA′===,
∴S阴=S扇CBC′﹣S△A′BC′﹣S扇DBA′==.
故选:C.
27.如图,点O是半圆圆心,BE是半圆的直径,点A,D在半圆上,且AD∥BO,∠ABO=60°,AB=8,过点D作DC⊥BE于点C,则阴影部分的面积是( )
A. B. C. D.
解:连接OA,
∵∠ABO=60°,OA=OB,
∴△AOB是等边三角形,
∵AB=8,∠AOB=60°,
∴⊙O的半径为8,∠AOE=120°,
∵AD∥OB,
∴∠OAD=∠AOB=60°,
∵OA=OD,
∴∠AOD=60°,
∵∠AOB=∠AOD=60°,
∴∠DOE=60°,
∵DC⊥BE于点C,
∴CD=OD=4,OC=OD=4,
∴BC=8+4=12,
∴S阴影=S△AOB+S扇形OAE﹣S△BCD
=×8×4+﹣×12×4
=﹣8,
故选:A.
28.如图,在正方形ABCD中,AC和BD交于点O,过点O的直线EF交AB于点E(E不与A,B重合),交CD于点F.以点O为圆心,OC为半径的圆交直线EF于点M,N.若AB=1,则图中阴影部分的面积为( )
A.﹣ B.﹣ C.﹣ D.﹣
解:以OD为半径作弧DN,
∵四边形ABCD是正方形,
∴OB=OD=OC,∠DOC=90°,
∵∠EOB=∠FOD,
∴S扇形BOM=S扇形DON,
∴S阴影=S扇形DOC﹣S△DOC=﹣×1×1=﹣,
故选:B.
29.如图,AB是半圆的直径,点C在直径上,以C为圆心、CA为半径向内作直角扇形,再以D为圆心、C为半径向内作直角扇形,使点E刚好落到半圆上,若AB=10,则阴影部分的面积为( )
A.16π B.12π C.8π D.4π
解:如图,过点E作EF⊥AB于点F,连接AE、BE,
∵AB是半圆的直径,
∴∠AEB=90°,即∠EAB+∠EBA=90°,
∵EF⊥AB,
∴∠AFE=∠EFB=90°,
∴∠EAB+∠AEF=90°,
∴∠EBA=∠AEF,
∴△AEF∽△EBF,
∴,即EF2=AF BF,
设AC=x,
∵EF⊥AB,且由作图可知阴影部分是两个半径相等的半圆,
∴四边形DCFE是正方形,
∴CD=DE=EF=CF=AC=x,
∴AF=2x,
∴BF=10﹣2x,
∴x2=2x(10﹣2x),
∴x1=0(舍),x2=4,
∴S阴影=2×=8π.
故选:C.
30.如图,在矩形ABCD中,AB=4,AB>BC,以点A为圆心、AB长为半径的弧BE与DC相交于点E,点E为DC的中点,则由BC、CE和弧BE围成的阴影部分图形的面积是( )
A. B. C. D.
解:由题意可得:AB=AE=CD=4,∠D=∠DAB=90°,
∵点E是DC的中点,
∴DE=2=,
∴∠DAE=30°,AD==,
∴∠EAB=∠DAB﹣∠DAE=90°﹣30°=60°,
∴S阴影=S矩形ABCD﹣SRt△ADE﹣S扇形ABE
=4×﹣﹣
=.
故选:A.
同课章节目录
