【整理推荐】华师大版 数学八年级上册 同步授课课件:141 勾股定理(共4课时)
文档属性
| 名称 | 【整理推荐】华师大版 数学八年级上册 同步授课课件:141 勾股定理(共4课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-02 00:00:00 | ||
图片预览








文档简介
课件44张PPT。华东师大版
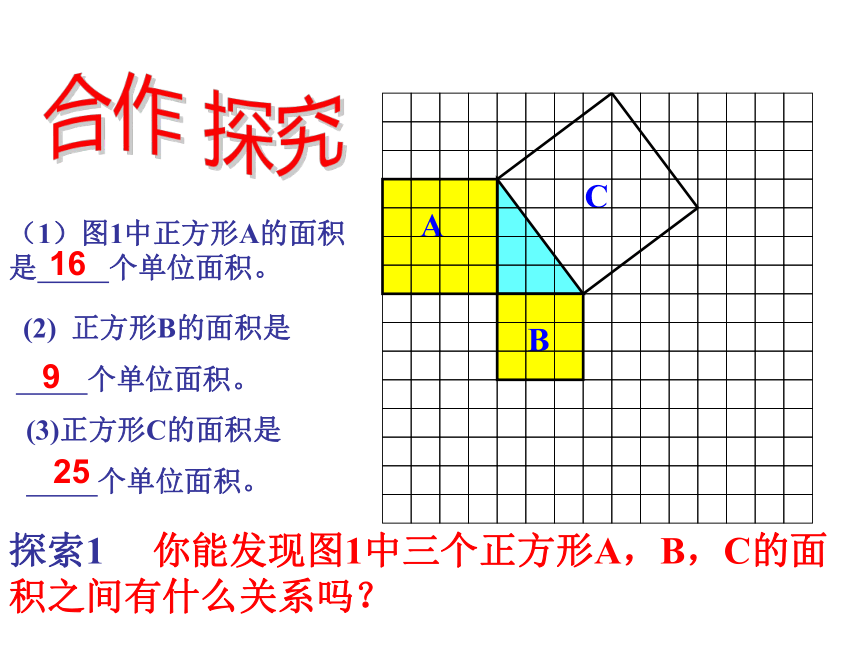
八年级(上)数学教学课件华东师大版八年级(上册)第14章 勾股定理14.1 勾股定理(第1课时)直角三角形三边的关系(1)图1中正方形A的面积是 个单位面积。 (2) 正方形B的面积是
个单位面积。(3)正方形C的面积是
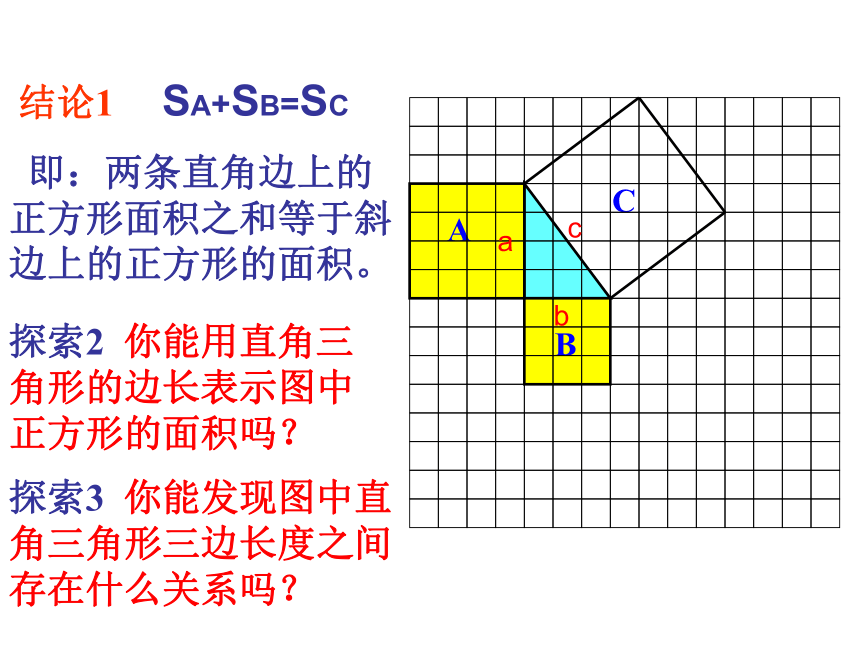
个单位面积。16925合作 探究探索1 你能发现图1中三个正方形A,B,C的面积之间有什么关系吗? 结论1 SA+SB=SC
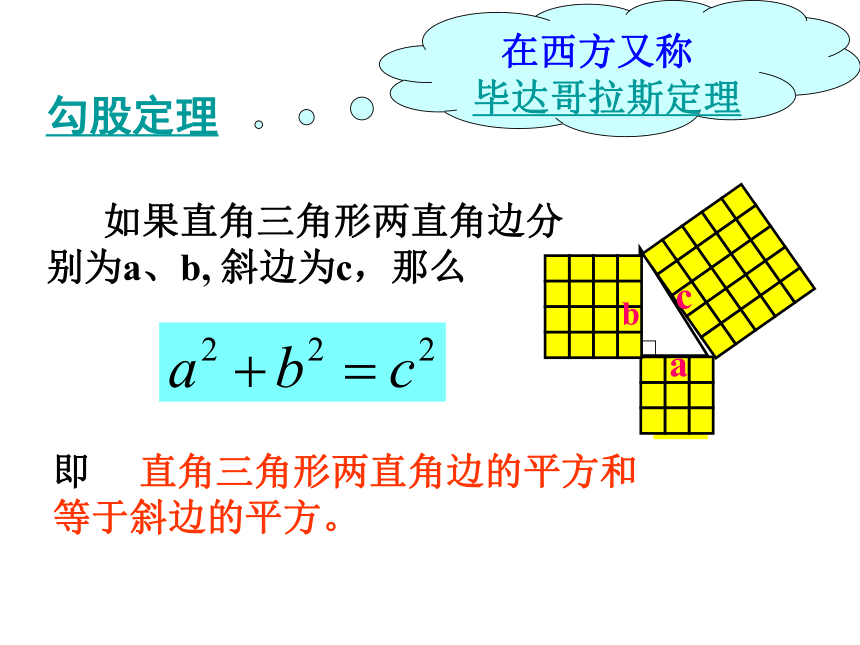
探索2 你能用直角三角形的边长表示图中正方形的面积吗?探索3 你能发现图中直角三角形三边长度之间存在什么关系吗?acb 即:两条直角边上的正方形面积之和等于斜边上的正方形的面积。勾股定理 如果直角三角形两直角边分别为a、b, 斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方。abc勾股弦bac在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.已知一个三角形斜边长17厘米、一条直角边长15厘米的
直角三角形,求这个三角形的面积.
解: 如 图, 设另一条直角边长是 x 厘米.由勾股定理得:
152 + x2 = 172而 x2 = 172 - 152= 289 – 225 = 64所以 :x=8直角三角形的面积是:
(平方厘米)习题讲解在一场强大的台风中,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
想一想1、下图中的三角形是直角三角形,其余是正方形,求下列图中字母所表示的正方形的面积.=625=144想一想 2. 小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?∴售货员没搞错∵荧屏对角线大约为74厘米4658算一算 如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。49? 议一议 美丽的勾股树(一)欣赏美丽的勾股树(二)欣赏 中国最早的一部数学著作《周髀(bì) 算经》中记录着在公元前1100年左右的西周时期数学家商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。” 后来人们就简单地把这个事实说成“勾三股四弦五”。这就是著名的勾股定理。
在稍后一点的《九章算术》( 约在 公元50至100年间)一书中,勾股定理得到了更加规范的一般性表达。书中的《勾股章》说:“把勾和股分别自乘,然后把它们的积加起来,再进行开方,便可以得到弦。”
我国最早对勾股定理进行证明的,是三国时期吴国的数学家赵爽。毕达哥拉斯 在国外,相传勾股定理是公元前550年古希腊数学家兼哲学家毕达哥拉斯首先发现的。因此又称此定理为“毕达哥拉斯定理”。但毕达哥拉斯对勾股定理的证明方法已经失传。且他发现的时间比我国要迟得多。 小结1、利用数格子的方法,探索了以直角三角形三边为边长的正方形面积的关系(即两个小正方形的面积之和等于大正方形的面积)2、探索了直角三角形的三边关系, 得到勾股定理:即直角三角形两直角边的平方和等于斜边的平方平A的面积+B的面积=C的面积a2+b2=c2总结反思布置作业你有何收获呢?精彩不断
创意无限华东师大版八年级(上册)第14章 勾股定理14.1 勾股定理(第2课时)直角三角形三边的关系2002年国际数学家大会会标赵爽
弦图2002年国际数学家大会会标思考:
1、中间小正方形的边长和面积分别是多少?
2、大正方形的面积可以看成哪几个图形面积相加得到?
3、根据上题可以写出怎样一个关系式?
?动手拼一拼即a2+b2=c2伽菲尔德
1881 年成为美国第 20 任总统
1876 年提出有关证明,
证法称为“总统”证法 例1 我方侦察员小王在距离东西方向公路400米处侦察,发现一辆汽车在公路上行驶,他赶紧拿出红外线测距仪,测得汽车与他相距400米,10秒后,汽车与他相距500米,你能帮小王计算敌方汽车的速度吗?典例精析例2 飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方4000米处,过了20秒,飞机距离这个男孩5000米,飞机每小时飞行多少千米?40005000学以致用ADBC34 1.已知∠ACB=Rt∠,
CD⊥AB,AC=3,BC=4.
求CD的长.我来试一试C2. 如图所示是某机械零件的平面图,尺寸如图所示, 求两孔中心A, B之间的距离.(单位:毫米)(1)直角三角形的两直角边为3和4,则斜边为___(3)直角三角形的两直角边为6和8,则斜边为___(2)直角三角形的两直角边为5和12,则斜边为___比一比谁最快(5)直角三角形的两条边为3和4,则斜边上的高是 。(4)直角三角形的两条边为3和4,则这个直角三角形的周长为 。1251013补充练习:
1、放学以后,小红和小颖从学校分手,分别沿着东南方向和西南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖用20分钟到家,小红和小颖家的距离为 ( )
A、600米; B、800米; C、1000米; D、不能确定
2、直角三角形两直角边分别为5厘米、12厘米,那么斜边上的高是 ( )
A、6厘米; B、 8厘米; C、 80/13厘米;D、 60/13厘米;
CD3、等腰三角形底边上的高为8,周长为32,求这个三角形的面积8DABC解:设这个三角形为ABC,高为AD,设BD为X,则AB为(16-X), 由勾股定理得:
X2+82=(16-X)2即X2+64=256-32X+X2∴ X=6∴ S?ABC=BC?AD/2=2 ?6 ?8/2=48你能想到不同的证明勾股定理的方法吗华东师大版八年级(上册)第14章 勾股定理14.1 勾股定理(第3课时)直角三角形的判定古埃及人曾用下面的方法得到直角:他们用13个等距离的结把一根绳子分成等长的12段,一个工匠同时握住第一个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处。做 一 做 下列的五组数分别是一个三角形的三边
长a,b,c:
①3,4,5; ②6,8,10;③5,12,13;
④7,24,25; ⑤ 8,15,17
(1)这三组数都满足a2+b2=c2吗?
(2)分别以每组数为三边作出三角形,用
量角器量一量,它们都是直角三角形吗? 如果三角形的三边长a,b,c 满足a2+b2=c2,那么这个三角形是
直角三角形。
其中满足a2+b2=c2的三个正整数, 称为勾股数。3、4、55、12、137、24、259、40、4111、60、6112、35、3716、63、6520、21、2928、45、5313、84、8533、56、6536、77、8520、99、1018、15、17常见勾股数例1 一个零件的形状如图1所示,按规定这个零件中,∠A和∠DBC都应为直角,工人师傅量得这个零件各边尺寸如图2所示,这个零件符合要求吗?图1图2解:∵在△ABD中,AB2+AD2=9+16=25=BD2
∴△ABD是直角三角形,∠A是直角
∵在△BCD中,BD2+BC2=25+144=169=CD2
∴△BCD是直角三角形,∠DBC是直角
因此这个零件符合要求随 堂 练 习1、下列几组数是勾股数的为( )。
(A)9,12,19 (B)1.5,2,2.5
(C)7,25,24 (D)12,18,22
2、一艘帆船在海上航行,由于风向的原因,帆船先向正东方向航行9千米,然后向正北方向航行40千米,这时它离开出发点_________千米。随 堂 练 习5、判断下列哪组数是勾股数:
(1)6,7,8; (2)8,15,6;
(3)a=n2-1,b=2n,c=n2+1 (n>1)
(4)a=m2-n2,b=2mn,c=m2+n2 (m>n>0)4、下列几组数能否作为直角三角形的三边长?说说你的理由。
(1)9,12,15; (2)15,36,39;
(3)12,35,36; (4)12,18,22。√√√√例2 一小船先向正南行进了80米到另一小船处借东西,之后又向正东行进了150米,此时它距出发地多少米?解:设它距出发地x米,
由勾股定理得:
x2=802+1502=28900=1702,
解得:x=170
此时小船距出发点170米.例3 如图,四边形ABCD中,AB⊥AD,已知AD=3cm,AB=4cm,CD=12cm,BC=13cm,求四边形ABCD 的面积。解:连接BD,在Rt△ABD中,
由勾股定理,得BD=5cm.
又因为在△ BDC中,三边分别是5,12,13,满足勾股定理的逆定理,所以△ BDC是直角三角形。因此四边形ABCD的面积为36平方厘米拓展演练1、如果三角形的三条线段a,b,c满足a2=c2-b2,这个三角形是直角三角形吗?为什么?
2、如果将直角三角形的三条边长同时扩大一个相同的倍数,得到的三角形还是直角三角形吗?填写下表,并计算第一列每组数是否为勾股数,她们的2倍、3倍、4倍、10倍呢?9,12,1512,16,2030,40,5010,24,2620,48,5250,120,13016,30,3424,45,5180,150,17014,48,5021,72,7528,96,1003、将一根长为24个单位的绳子,分别标出A,B,C,D四个点,它们将绳子分成长为6个单位、8个单位和10个单位的三条线段,自己握住绳子的两个端点(A点和D点),两名同伴分别握住B点和C点,一起将绳子拉直,会得到一个什么形状的三角形?为什么?因为三边满足勾股定理.4、假期中,王强和同学到某海岛上去探宝旅游,按照探宝图(如图),他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,再折向北走到6千米处往东一拐,仅走1千米就找到了宝藏,问登陆点A到宝藏埋藏点B的直线距离是多少千米?82361CBC=6+2=8AC=8-3+1=6AB2=AC2+BC2=36+64=100∴ AC=10(千米)
八年级(上)数学教学课件华东师大版八年级(上册)第14章 勾股定理14.1 勾股定理(第1课时)直角三角形三边的关系(1)图1中正方形A的面积是 个单位面积。 (2) 正方形B的面积是
个单位面积。(3)正方形C的面积是
个单位面积。16925合作 探究探索1 你能发现图1中三个正方形A,B,C的面积之间有什么关系吗? 结论1 SA+SB=SC
探索2 你能用直角三角形的边长表示图中正方形的面积吗?探索3 你能发现图中直角三角形三边长度之间存在什么关系吗?acb 即:两条直角边上的正方形面积之和等于斜边上的正方形的面积。勾股定理 如果直角三角形两直角边分别为a、b, 斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方。abc勾股弦bac在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.已知一个三角形斜边长17厘米、一条直角边长15厘米的
直角三角形,求这个三角形的面积.
解: 如 图, 设另一条直角边长是 x 厘米.由勾股定理得:
152 + x2 = 172而 x2 = 172 - 152= 289 – 225 = 64所以 :x=8直角三角形的面积是:
(平方厘米)习题讲解在一场强大的台风中,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
想一想1、下图中的三角形是直角三角形,其余是正方形,求下列图中字母所表示的正方形的面积.=625=144想一想 2. 小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?∴售货员没搞错∵荧屏对角线大约为74厘米4658算一算 如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。49? 议一议 美丽的勾股树(一)欣赏美丽的勾股树(二)欣赏 中国最早的一部数学著作《周髀(bì) 算经》中记录着在公元前1100年左右的西周时期数学家商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。” 后来人们就简单地把这个事实说成“勾三股四弦五”。这就是著名的勾股定理。
在稍后一点的《九章算术》( 约在 公元50至100年间)一书中,勾股定理得到了更加规范的一般性表达。书中的《勾股章》说:“把勾和股分别自乘,然后把它们的积加起来,再进行开方,便可以得到弦。”
我国最早对勾股定理进行证明的,是三国时期吴国的数学家赵爽。毕达哥拉斯 在国外,相传勾股定理是公元前550年古希腊数学家兼哲学家毕达哥拉斯首先发现的。因此又称此定理为“毕达哥拉斯定理”。但毕达哥拉斯对勾股定理的证明方法已经失传。且他发现的时间比我国要迟得多。 小结1、利用数格子的方法,探索了以直角三角形三边为边长的正方形面积的关系(即两个小正方形的面积之和等于大正方形的面积)2、探索了直角三角形的三边关系, 得到勾股定理:即直角三角形两直角边的平方和等于斜边的平方平A的面积+B的面积=C的面积a2+b2=c2总结反思布置作业你有何收获呢?精彩不断
创意无限华东师大版八年级(上册)第14章 勾股定理14.1 勾股定理(第2课时)直角三角形三边的关系2002年国际数学家大会会标赵爽
弦图2002年国际数学家大会会标思考:
1、中间小正方形的边长和面积分别是多少?
2、大正方形的面积可以看成哪几个图形面积相加得到?
3、根据上题可以写出怎样一个关系式?
?动手拼一拼即a2+b2=c2伽菲尔德
1881 年成为美国第 20 任总统
1876 年提出有关证明,
证法称为“总统”证法 例1 我方侦察员小王在距离东西方向公路400米处侦察,发现一辆汽车在公路上行驶,他赶紧拿出红外线测距仪,测得汽车与他相距400米,10秒后,汽车与他相距500米,你能帮小王计算敌方汽车的速度吗?典例精析例2 飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方4000米处,过了20秒,飞机距离这个男孩5000米,飞机每小时飞行多少千米?40005000学以致用ADBC34 1.已知∠ACB=Rt∠,
CD⊥AB,AC=3,BC=4.
求CD的长.我来试一试C2. 如图所示是某机械零件的平面图,尺寸如图所示, 求两孔中心A, B之间的距离.(单位:毫米)(1)直角三角形的两直角边为3和4,则斜边为___(3)直角三角形的两直角边为6和8,则斜边为___(2)直角三角形的两直角边为5和12,则斜边为___比一比谁最快(5)直角三角形的两条边为3和4,则斜边上的高是 。(4)直角三角形的两条边为3和4,则这个直角三角形的周长为 。1251013补充练习:
1、放学以后,小红和小颖从学校分手,分别沿着东南方向和西南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖用20分钟到家,小红和小颖家的距离为 ( )
A、600米; B、800米; C、1000米; D、不能确定
2、直角三角形两直角边分别为5厘米、12厘米,那么斜边上的高是 ( )
A、6厘米; B、 8厘米; C、 80/13厘米;D、 60/13厘米;
CD3、等腰三角形底边上的高为8,周长为32,求这个三角形的面积8DABC解:设这个三角形为ABC,高为AD,设BD为X,则AB为(16-X), 由勾股定理得:
X2+82=(16-X)2即X2+64=256-32X+X2∴ X=6∴ S?ABC=BC?AD/2=2 ?6 ?8/2=48你能想到不同的证明勾股定理的方法吗华东师大版八年级(上册)第14章 勾股定理14.1 勾股定理(第3课时)直角三角形的判定古埃及人曾用下面的方法得到直角:他们用13个等距离的结把一根绳子分成等长的12段,一个工匠同时握住第一个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处。做 一 做 下列的五组数分别是一个三角形的三边
长a,b,c:
①3,4,5; ②6,8,10;③5,12,13;
④7,24,25; ⑤ 8,15,17
(1)这三组数都满足a2+b2=c2吗?
(2)分别以每组数为三边作出三角形,用
量角器量一量,它们都是直角三角形吗? 如果三角形的三边长a,b,c 满足a2+b2=c2,那么这个三角形是
直角三角形。
其中满足a2+b2=c2的三个正整数, 称为勾股数。3、4、55、12、137、24、259、40、4111、60、6112、35、3716、63、6520、21、2928、45、5313、84、8533、56、6536、77、8520、99、1018、15、17常见勾股数例1 一个零件的形状如图1所示,按规定这个零件中,∠A和∠DBC都应为直角,工人师傅量得这个零件各边尺寸如图2所示,这个零件符合要求吗?图1图2解:∵在△ABD中,AB2+AD2=9+16=25=BD2
∴△ABD是直角三角形,∠A是直角
∵在△BCD中,BD2+BC2=25+144=169=CD2
∴△BCD是直角三角形,∠DBC是直角
因此这个零件符合要求随 堂 练 习1、下列几组数是勾股数的为( )。
(A)9,12,19 (B)1.5,2,2.5
(C)7,25,24 (D)12,18,22
2、一艘帆船在海上航行,由于风向的原因,帆船先向正东方向航行9千米,然后向正北方向航行40千米,这时它离开出发点_________千米。随 堂 练 习5、判断下列哪组数是勾股数:
(1)6,7,8; (2)8,15,6;
(3)a=n2-1,b=2n,c=n2+1 (n>1)
(4)a=m2-n2,b=2mn,c=m2+n2 (m>n>0)4、下列几组数能否作为直角三角形的三边长?说说你的理由。
(1)9,12,15; (2)15,36,39;
(3)12,35,36; (4)12,18,22。√√√√例2 一小船先向正南行进了80米到另一小船处借东西,之后又向正东行进了150米,此时它距出发地多少米?解:设它距出发地x米,
由勾股定理得:
x2=802+1502=28900=1702,
解得:x=170
此时小船距出发点170米.例3 如图,四边形ABCD中,AB⊥AD,已知AD=3cm,AB=4cm,CD=12cm,BC=13cm,求四边形ABCD 的面积。解:连接BD,在Rt△ABD中,
由勾股定理,得BD=5cm.
又因为在△ BDC中,三边分别是5,12,13,满足勾股定理的逆定理,所以△ BDC是直角三角形。因此四边形ABCD的面积为36平方厘米拓展演练1、如果三角形的三条线段a,b,c满足a2=c2-b2,这个三角形是直角三角形吗?为什么?
2、如果将直角三角形的三条边长同时扩大一个相同的倍数,得到的三角形还是直角三角形吗?填写下表,并计算第一列每组数是否为勾股数,她们的2倍、3倍、4倍、10倍呢?9,12,1512,16,2030,40,5010,24,2620,48,5250,120,13016,30,3424,45,5180,150,17014,48,5021,72,7528,96,1003、将一根长为24个单位的绳子,分别标出A,B,C,D四个点,它们将绳子分成长为6个单位、8个单位和10个单位的三条线段,自己握住绳子的两个端点(A点和D点),两名同伴分别握住B点和C点,一起将绳子拉直,会得到一个什么形状的三角形?为什么?因为三边满足勾股定理.4、假期中,王强和同学到某海岛上去探宝旅游,按照探宝图(如图),他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,再折向北走到6千米处往东一拐,仅走1千米就找到了宝藏,问登陆点A到宝藏埋藏点B的直线距离是多少千米?82361CBC=6+2=8AC=8-3+1=6AB2=AC2+BC2=36+64=100∴ AC=10(千米)
