北师大版数学七年级上册 第二章 有理数及其运算 过关训练课件(共26张PPT)
文档属性
| 名称 | 北师大版数学七年级上册 第二章 有理数及其运算 过关训练课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 868.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-09 14:22:17 | ||
图片预览








文档简介
(共26张PPT)
第二章 有理数及其运算过关训练
过关训练+综合训练
B
A
3.一天早晨的气温是-7 ℃,中午上升了11 ℃,半夜又下降了9 ℃,则半夜的气温是( )
A.4 ℃ B.-5 ℃ C.13 ℃ D.-13 ℃
4.一个整数用科学记数法表示为1.234 5×1010,则原数中“0”的个数为( )
A.4 B.6 C.8 D.10
B
B
D
D
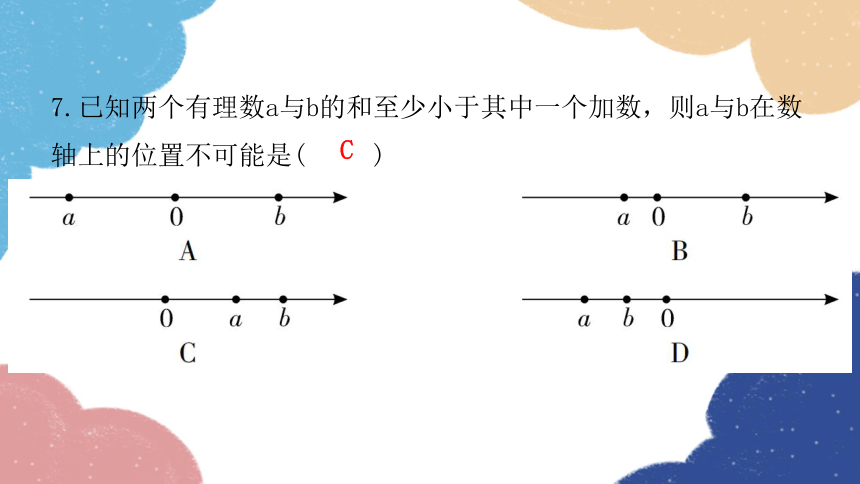
7.已知两个有理数a与b的和至少小于其中一个加数,则a与b在数轴上的位置不可能是( )
C
8.若a=-3×42,b=(-3×4)2,c=-(3×4)2,则a,b,c的大小关系正确的是( )
A.c>a>b B.b>c>a C.a>b>c D.b>a>c
D
9.利用计算器可计算出72=49,672=4 489,6672=444 889,6 6672=44 448 889,则66 6672=( )
A.4 444 488 889 B.4 444 488 899
C.444 488 889 D.4 444 888 889
A
10.将一把刻度尺按如图S2-1所示放在数轴上(数轴的单位长度是1 cm),刻度尺上的“0 cm”和“8 cm”分别对应数轴上的-3.6和x,则x的值为( )
A.4.2 B.4.3 C.4.4 D.4.5
C
13.如图S2-2,小明写作业时不慎将墨水滴在数轴上,墨迹盖住部分的整数共有_____个.
7
14.小明与小刚规定了一种新运算△:a△b=3a-2b.按照运算规则,小明计算出2△5=-4,请你帮小刚计算2△(-5)=_______.
15.在如图S2-3所示的正方形数阵中规定运算:16-4=2×6,若a=10,则b=_______.
16
1
-3,
-1
0,
...
2,
-(-3)
18.已知:|a|=3,|b|=2,且a<b,求(a+b)3的值.
解:因为|a|=3,
所以a=±3.
因为|b|=2,
所以b=±2.
又因为a<b,
所以a=-3,b=±2.
所以①当a=-3,b=2时,(a+b)3=(-3+2)3=-1;
②当a=-3,b=-2时,(a+b)3=(-3-2)3=-53=-125.
综上所述,(a+b)3的值为-1或-125.
四、解答题(二)(本大题3小题,每小题9分,共27分)
19.计算:
(1)-12+11-8+39;
解:原式=(-12-8)+(11+39)
=-20+50
=30.
21.今年国庆,重庆再次成为了人气爆棚旅游目的地,其中作为“网红打卡地”的解放碑商圈在十一假期首日(10月1日)人流量达到40万人次,我市文旅部持续记录了10月2日~7日解放碑商圈的人流量变化情况:(用正数表示比前一天上升数,负数表示比前一天下降数)
日期 2 3 4 5 6 7
人流量变化/万人次 +5.4 +4.7 -2.6 +4.8 -3.5 -12.9
(1)“十一”期间解放碑商圈哪一天人流量最大?人流量是多少?
解:(1)10月2日人流量是40+5.4=45.4(万人次),
10月3日人流量是45.4+4.7=50.1(万人次),
10月4日人流量是50.1-2.6=47.5(万人次),
10月5日人流量是47.5+4.8=52.3(万人次),
10月6日人流量是52.3-3.5=48.8(万人次),
10月7日人流量是48.8-12.9=35.9(万人次).
答:10月5日人流量最大,是52.3万人次.
(2)据统计解放碑商圈“十一”期间人均每日消费72元,请问“十一”期间(10月1日~7日)解放碑商圈总收入为多少万元?
(2)总收入为(40+45.4+50.1+47.5+52.3+48.8+35.9)×72=23 040(万元).
答:“十一”期间解放碑商圈总收入为23 040万元.
五、解答题(三)(本大题2小题,每小题12分,共24分)
22.设用符号(a,b)表示a,b两数中较小的一个,用符号[a,b]表示a,b两数中较大的一个,如(-2,1)=-2,[-3,5]=5.小红求解(-5,-3)+[5,1]+[-4,(-2,-7)]的过程如下:
原式=-3+5+[-4,-7]=-3+5+(-7)=-5
(1)小红的计算过程正确吗?若不正确,请给出正确的解答;
解:(1)不正确.正确解答如下:
原式=-5+5+[-4,-7]=-5+5+(-4)=-4.
(2)仿照上面的规定,构造一个含分数和负数的算式,并求解.
23.如图S2-4,在数轴上点A表示的数是8,若动点P从原点O出发,以2个单位/s的速度向左运动,同时另一动点Q从点A出发,以4个单位/s的速度也向左运动,到达原点后立即以原来的速度返回,向右运动,设运动的时间为t(s).
(1)当t=0.5时,求点Q到原点O的距离;
解:(1)当t=0.5时,AQ=4t=4×0.5=2.
因为OA=8,
所以OQ=OA-AQ=8-2=6.
所以点Q到原点O的距离为6.
(2)当t=2.5时,求点Q到原点O的距离;
(2)当t=2.5时,点Q运动的距离为4t=4×2.5=10.
因为OA=8,
所以OQ=10-8=2.
所以点Q到原点O的距离为2.
(3)当点Q到原点O的距离为4时,求点P到原点O的距离.
(3)当点Q到原点O的距离为4时,即OQ=4.
①当点Q向左运动时,OA=8,则AQ=4.
所以t=1.
所以OP=2;
②当点Q向右运动时,OQ=4,
所以点Q运动的距离是8+4=12.
所以t=12÷4=3.
所以OP=2×3=6.
综上所述,点P到原点O的距离为2或6.
谢 谢!
第二章 有理数及其运算过关训练
过关训练+综合训练
B
A
3.一天早晨的气温是-7 ℃,中午上升了11 ℃,半夜又下降了9 ℃,则半夜的气温是( )
A.4 ℃ B.-5 ℃ C.13 ℃ D.-13 ℃
4.一个整数用科学记数法表示为1.234 5×1010,则原数中“0”的个数为( )
A.4 B.6 C.8 D.10
B
B
D
D
7.已知两个有理数a与b的和至少小于其中一个加数,则a与b在数轴上的位置不可能是( )
C
8.若a=-3×42,b=(-3×4)2,c=-(3×4)2,则a,b,c的大小关系正确的是( )
A.c>a>b B.b>c>a C.a>b>c D.b>a>c
D
9.利用计算器可计算出72=49,672=4 489,6672=444 889,6 6672=44 448 889,则66 6672=( )
A.4 444 488 889 B.4 444 488 899
C.444 488 889 D.4 444 888 889
A
10.将一把刻度尺按如图S2-1所示放在数轴上(数轴的单位长度是1 cm),刻度尺上的“0 cm”和“8 cm”分别对应数轴上的-3.6和x,则x的值为( )
A.4.2 B.4.3 C.4.4 D.4.5
C
13.如图S2-2,小明写作业时不慎将墨水滴在数轴上,墨迹盖住部分的整数共有_____个.
7
14.小明与小刚规定了一种新运算△:a△b=3a-2b.按照运算规则,小明计算出2△5=-4,请你帮小刚计算2△(-5)=_______.
15.在如图S2-3所示的正方形数阵中规定运算:16-4=2×6,若a=10,则b=_______.
16
1
-3,
-1
0,
...
2,
-(-3)
18.已知:|a|=3,|b|=2,且a<b,求(a+b)3的值.
解:因为|a|=3,
所以a=±3.
因为|b|=2,
所以b=±2.
又因为a<b,
所以a=-3,b=±2.
所以①当a=-3,b=2时,(a+b)3=(-3+2)3=-1;
②当a=-3,b=-2时,(a+b)3=(-3-2)3=-53=-125.
综上所述,(a+b)3的值为-1或-125.
四、解答题(二)(本大题3小题,每小题9分,共27分)
19.计算:
(1)-12+11-8+39;
解:原式=(-12-8)+(11+39)
=-20+50
=30.
21.今年国庆,重庆再次成为了人气爆棚旅游目的地,其中作为“网红打卡地”的解放碑商圈在十一假期首日(10月1日)人流量达到40万人次,我市文旅部持续记录了10月2日~7日解放碑商圈的人流量变化情况:(用正数表示比前一天上升数,负数表示比前一天下降数)
日期 2 3 4 5 6 7
人流量变化/万人次 +5.4 +4.7 -2.6 +4.8 -3.5 -12.9
(1)“十一”期间解放碑商圈哪一天人流量最大?人流量是多少?
解:(1)10月2日人流量是40+5.4=45.4(万人次),
10月3日人流量是45.4+4.7=50.1(万人次),
10月4日人流量是50.1-2.6=47.5(万人次),
10月5日人流量是47.5+4.8=52.3(万人次),
10月6日人流量是52.3-3.5=48.8(万人次),
10月7日人流量是48.8-12.9=35.9(万人次).
答:10月5日人流量最大,是52.3万人次.
(2)据统计解放碑商圈“十一”期间人均每日消费72元,请问“十一”期间(10月1日~7日)解放碑商圈总收入为多少万元?
(2)总收入为(40+45.4+50.1+47.5+52.3+48.8+35.9)×72=23 040(万元).
答:“十一”期间解放碑商圈总收入为23 040万元.
五、解答题(三)(本大题2小题,每小题12分,共24分)
22.设用符号(a,b)表示a,b两数中较小的一个,用符号[a,b]表示a,b两数中较大的一个,如(-2,1)=-2,[-3,5]=5.小红求解(-5,-3)+[5,1]+[-4,(-2,-7)]的过程如下:
原式=-3+5+[-4,-7]=-3+5+(-7)=-5
(1)小红的计算过程正确吗?若不正确,请给出正确的解答;
解:(1)不正确.正确解答如下:
原式=-5+5+[-4,-7]=-5+5+(-4)=-4.
(2)仿照上面的规定,构造一个含分数和负数的算式,并求解.
23.如图S2-4,在数轴上点A表示的数是8,若动点P从原点O出发,以2个单位/s的速度向左运动,同时另一动点Q从点A出发,以4个单位/s的速度也向左运动,到达原点后立即以原来的速度返回,向右运动,设运动的时间为t(s).
(1)当t=0.5时,求点Q到原点O的距离;
解:(1)当t=0.5时,AQ=4t=4×0.5=2.
因为OA=8,
所以OQ=OA-AQ=8-2=6.
所以点Q到原点O的距离为6.
(2)当t=2.5时,求点Q到原点O的距离;
(2)当t=2.5时,点Q运动的距离为4t=4×2.5=10.
因为OA=8,
所以OQ=10-8=2.
所以点Q到原点O的距离为2.
(3)当点Q到原点O的距离为4时,求点P到原点O的距离.
(3)当点Q到原点O的距离为4时,即OQ=4.
①当点Q向左运动时,OA=8,则AQ=4.
所以t=1.
所以OP=2;
②当点Q向右运动时,OQ=4,
所以点Q运动的距离是8+4=12.
所以t=12÷4=3.
所以OP=2×3=6.
综上所述,点P到原点O的距离为2或6.
谢 谢!
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
