相似三角形判定(SAS)[下学期]
文档属性
| 名称 | 相似三角形判定(SAS)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 40.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-01-09 10:20:00 | ||
图片预览


文档简介
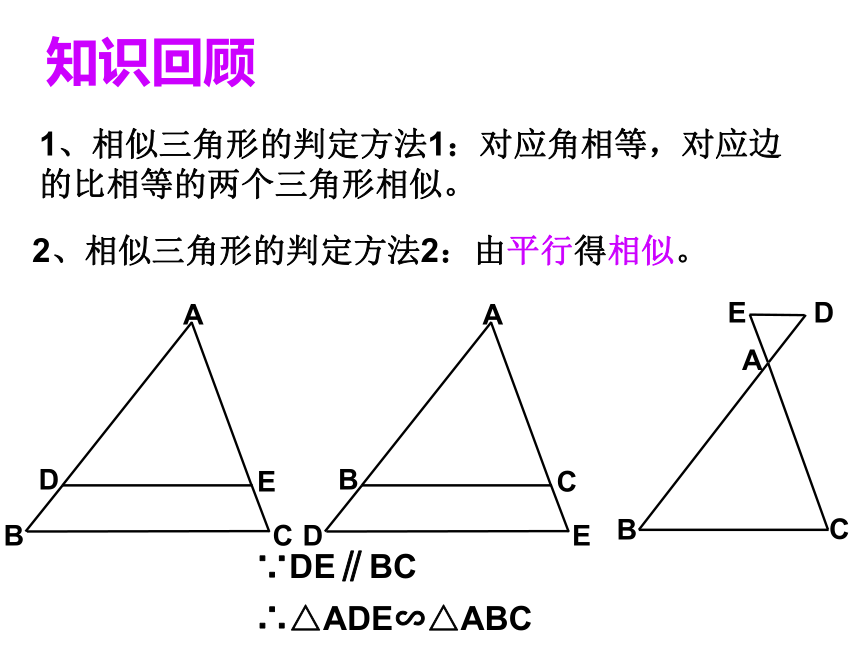
课件12张PPT。相似三角形的判定∵DE∥BC
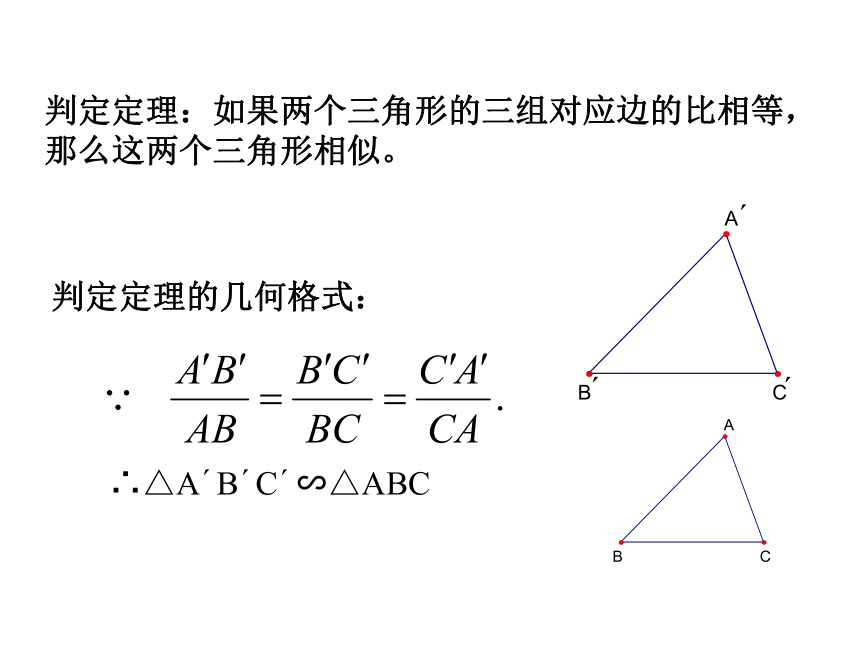
∴△ADE∽△ABC1、相似三角形的判定方法1:对应角相等,对应边的比相等的两个三角形相似。知识回顾2、相似三角形的判定方法2:由平行得相似。判定定理:如果两个三角形的三组对应边的比相等,那么这两个三角形相似。判定定理的几何格式:∴△A′B′C′∽△ABC 学习三角形全等时,我们知道,除了可以通过证明三组对应角相等,三组对应边相等来判定两个三角形全等外,判定的简便方法有哪些?SSS SAS ASA AAS类似地,判定两个三角形相似时,是不是对所有
的对应角和对应边都要一一验证呢?类似于判定三角形全等的SSS方法,我们能
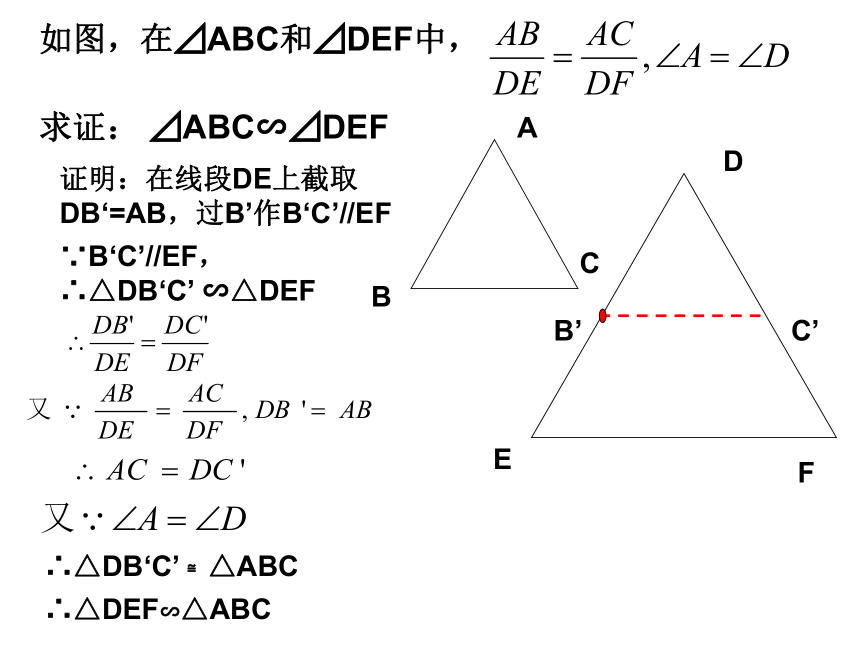
不能通过三边来判断两个三角形相似呢?如图,在⊿ABC和⊿DEF中,
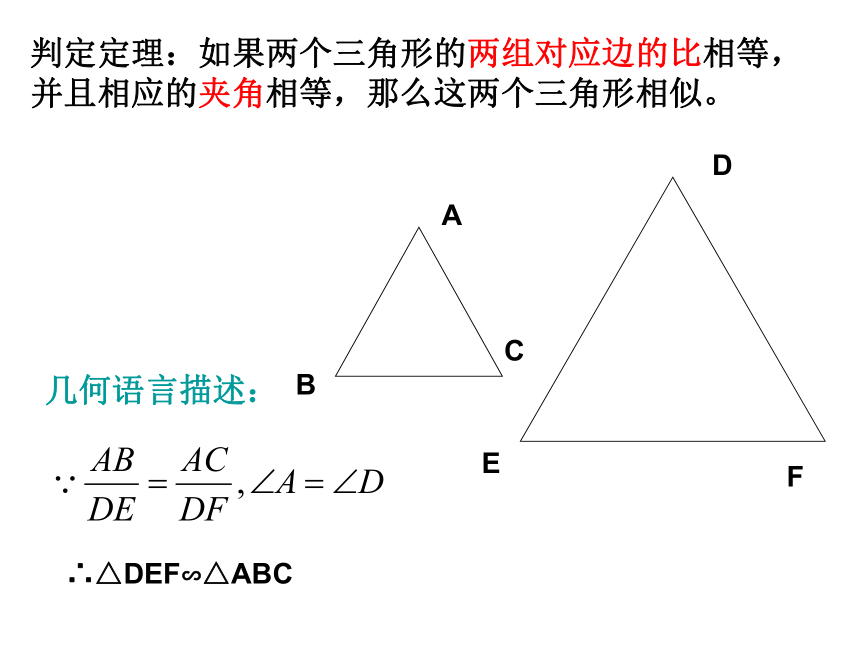
求证: ⊿ABC∽⊿DEFC’证明:在线段DE上截取DB‘=AB,过B’作B‘C’//EF∵B‘C’//EF,∴△DB‘C’ ∽△DEF∴△DB‘C’ ≌△ABC∴△DEF∽△ABC判定定理:如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似。∴△DEF∽△ABC几何语言描述:例1.依据下列各组条件,判定△ABC与△A′B′C′是不是相似,并说明为什么:
(1)AB=4厘米, BC=6厘米, ∠B=550,
A′B′=12厘米,B′C′=18厘米, ∠B′=550(2)AB=4厘米, BC=6厘米, AC=9厘米,
A′B′=12厘米,B′C′=18厘米,A′C′=24厘米(3)AB=6厘米, BC=9厘米, ∠B=550,
A′B′=12厘米,B′C′=18厘米, ∠A′=550(4)AB=6厘米, AC=9厘米, ∠B=550,
A′B′=12厘米,A′C′=18厘米, ∠B′=550EBFAC△AFE∽△ABCEBACABCOEFG求证:△EFG∽△ABC本节课你的收获是?学会了利用三角形三边的比来判定三角形是否相似的方法化归的思想分类讨论的思想方法相似三角形的判定方法:1、相似三角形的判定方法1:对应角相等,对应边的比相等的两个三角形相似。2、相似三角形的判定方法2:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似。3、相似三角形的判定方法3:如果两个三角形的三组对应边的比相等,那么这两个三角形相似。判定定理:如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似。
∴△ADE∽△ABC1、相似三角形的判定方法1:对应角相等,对应边的比相等的两个三角形相似。知识回顾2、相似三角形的判定方法2:由平行得相似。判定定理:如果两个三角形的三组对应边的比相等,那么这两个三角形相似。判定定理的几何格式:∴△A′B′C′∽△ABC 学习三角形全等时,我们知道,除了可以通过证明三组对应角相等,三组对应边相等来判定两个三角形全等外,判定的简便方法有哪些?SSS SAS ASA AAS类似地,判定两个三角形相似时,是不是对所有
的对应角和对应边都要一一验证呢?类似于判定三角形全等的SSS方法,我们能
不能通过三边来判断两个三角形相似呢?如图,在⊿ABC和⊿DEF中,
求证: ⊿ABC∽⊿DEFC’证明:在线段DE上截取DB‘=AB,过B’作B‘C’//EF∵B‘C’//EF,∴△DB‘C’ ∽△DEF∴△DB‘C’ ≌△ABC∴△DEF∽△ABC判定定理:如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似。∴△DEF∽△ABC几何语言描述:例1.依据下列各组条件,判定△ABC与△A′B′C′是不是相似,并说明为什么:
(1)AB=4厘米, BC=6厘米, ∠B=550,
A′B′=12厘米,B′C′=18厘米, ∠B′=550(2)AB=4厘米, BC=6厘米, AC=9厘米,
A′B′=12厘米,B′C′=18厘米,A′C′=24厘米(3)AB=6厘米, BC=9厘米, ∠B=550,
A′B′=12厘米,B′C′=18厘米, ∠A′=550(4)AB=6厘米, AC=9厘米, ∠B=550,
A′B′=12厘米,A′C′=18厘米, ∠B′=550EBFAC△AFE∽△ABCEBACABCOEFG求证:△EFG∽△ABC本节课你的收获是?学会了利用三角形三边的比来判定三角形是否相似的方法化归的思想分类讨论的思想方法相似三角形的判定方法:1、相似三角形的判定方法1:对应角相等,对应边的比相等的两个三角形相似。2、相似三角形的判定方法2:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似。3、相似三角形的判定方法3:如果两个三角形的三组对应边的比相等,那么这两个三角形相似。判定定理:如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似。
