相似三角形的应用1[下学期]
文档属性
| 名称 | 相似三角形的应用1[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 560.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-01-16 18:15:00 | ||
图片预览




文档简介
课件13张PPT。 相似三角形的应用(一) 估算河的宽度此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB.ADCEB走近河流小小旅行家: 我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.?
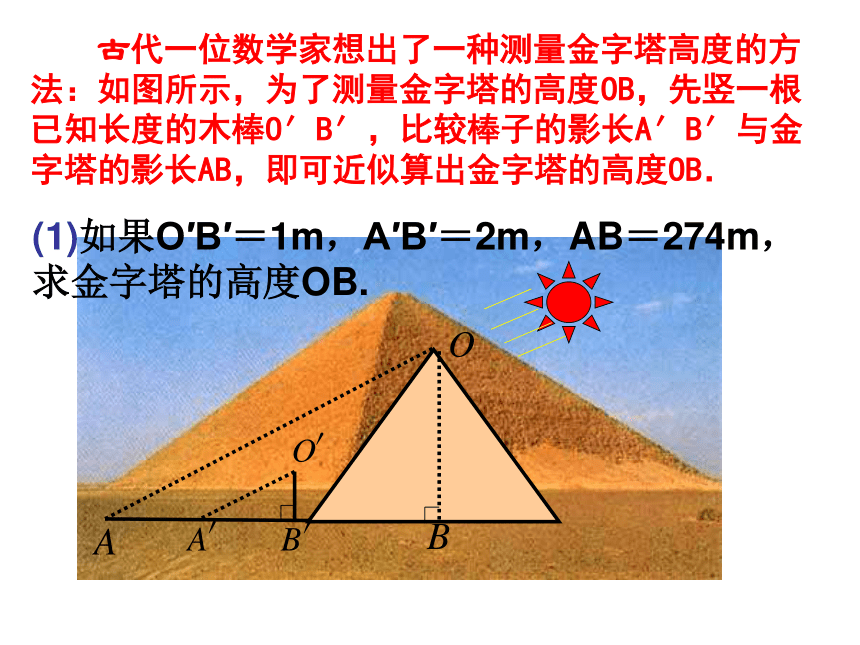
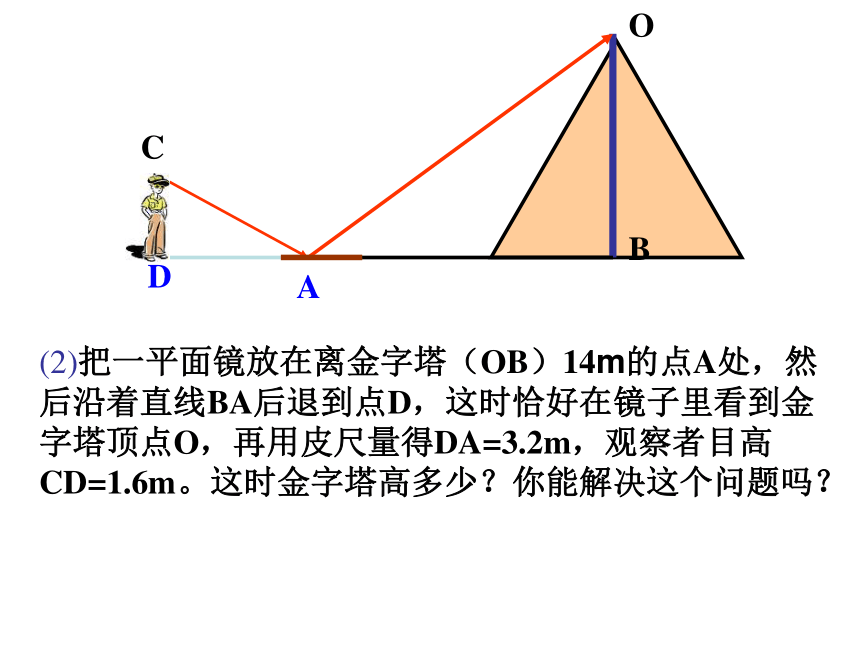
胡夫金字塔是埃及现存规模最大的金字塔,被喻为“世界古代七大奇观之一”。塔的4个斜面正对东南西北四个方向,塔基呈正方形,每边长约230多米。据考证,为建成大金字塔,共动用了10万人花了20年时间.原高146.59米,但由于经过几千年的风吹雨打,顶端被风化吹蚀.所以高度有所降低 。 小小旅行家:走近金字塔 埃及著名的考古专家穆罕穆德决定重新测量胡夫金字塔的高度.在一个烈日高照的上午.他和儿子小穆罕穆德来到了金字塔脚下,他想考一考年仅14岁的小穆罕穆德.给你一条1米高的木杆,一把皮尺,一面平面镜.你能利用所学知识来测出塔高吗?1米木杆皮尺平面镜 古代一位数学家想出了一种测量金字塔高度的方法:如图所示,为了测量金字塔的高度OB,先竖一根已知长度的木棒O′B′,比较棒子的影长A′B′与金字塔的影长AB,即可近似算出金字塔的高度OB.(1)如果O′B′=1m,A′B′=2m,AB=274m,求金字塔的高度OB.OBADC(2)把一平面镜放在离金字塔(OB)14m的点A处,然后沿着直线BA后退到点D,这时恰好在镜子里看到金字塔顶点O,再用皮尺量得DA=3.2m,观察者目高CD=1.6m。这时金字塔高多少?你能解决这个问题吗? 1、如图,小明在打网球时,使球恰好能打过网,而且落在离网5米的位置上,求球拍击球的高度h.课堂练习2 、为了测量一河的宽AB,在河对岸选定一目标点A,再在河的一边选点D和 E,使DE⊥AD,然后,再选点B,作BC∥DE,与视线EA相交于点C。此时,测得DE=90m , BC=60m, BD=45m, 求两岸间的大致距离AB。3、(2006淄博市)如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B时,人影的长度( )
A.增大1.5米 B. 减小1.5米
C. 增大3.5米 D. 减小3.5米课堂练习 3.如图:小明想测量电线杆AB的高度,发现电线杆的影子恰好落在土坡的坡面CD和地面CB上,测得CD=4m,BC=10m,CD与地面成30度角,且此时测得1米杆子的影子长为2米,那么电线杆的高度是多少?ABDC课堂练习课堂小结:一 、相似三角形的应用主要有如下两个方面
1 测高(不能直接使用皮尺或刻度尺量的)
2 测距(不能直接测量的两点间的距离)、测高的方法
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长的比例”的原理解决 、测距的方法
测量不能到达两点间的距离,常构造相似三角形求解小明在晚上由路灯A走向路灯B,当他走到P时,发现身后他的影子的顶部刚好接触路灯A的底部;当他再向前走12米到达Q时,发现身前他的影子的顶部刚好接触到路灯B的底部,已知小明的身高是1.6米,两个路灯高9.6米,且AP=QB=x米
(1)求两灯的距离
(2)当小明走到路灯B时,他在路灯A的影长为多少?(2006年茂名市)如图,李华晚上在路灯下散步.已知李华的身高AB=h,灯柱的高OP=O/P/=l,两灯柱之间的距离OO/=m.
(l)若李华距灯柱OP的水平距离OA=a,求他影子AC的长;
(2)若李华在两路灯之间行走,则他前后的两个影子的长度之和(DA+AC)是否是定值?请说明理由;
(3)若李华在点A朝着影子(如图箭头)的方向以匀速行走,试求他影子的顶端在地面上移动的速度. 努力现在,成就未来
胡夫金字塔是埃及现存规模最大的金字塔,被喻为“世界古代七大奇观之一”。塔的4个斜面正对东南西北四个方向,塔基呈正方形,每边长约230多米。据考证,为建成大金字塔,共动用了10万人花了20年时间.原高146.59米,但由于经过几千年的风吹雨打,顶端被风化吹蚀.所以高度有所降低 。 小小旅行家:走近金字塔 埃及著名的考古专家穆罕穆德决定重新测量胡夫金字塔的高度.在一个烈日高照的上午.他和儿子小穆罕穆德来到了金字塔脚下,他想考一考年仅14岁的小穆罕穆德.给你一条1米高的木杆,一把皮尺,一面平面镜.你能利用所学知识来测出塔高吗?1米木杆皮尺平面镜 古代一位数学家想出了一种测量金字塔高度的方法:如图所示,为了测量金字塔的高度OB,先竖一根已知长度的木棒O′B′,比较棒子的影长A′B′与金字塔的影长AB,即可近似算出金字塔的高度OB.(1)如果O′B′=1m,A′B′=2m,AB=274m,求金字塔的高度OB.OBADC(2)把一平面镜放在离金字塔(OB)14m的点A处,然后沿着直线BA后退到点D,这时恰好在镜子里看到金字塔顶点O,再用皮尺量得DA=3.2m,观察者目高CD=1.6m。这时金字塔高多少?你能解决这个问题吗? 1、如图,小明在打网球时,使球恰好能打过网,而且落在离网5米的位置上,求球拍击球的高度h.课堂练习2 、为了测量一河的宽AB,在河对岸选定一目标点A,再在河的一边选点D和 E,使DE⊥AD,然后,再选点B,作BC∥DE,与视线EA相交于点C。此时,测得DE=90m , BC=60m, BD=45m, 求两岸间的大致距离AB。3、(2006淄博市)如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B时,人影的长度( )
A.增大1.5米 B. 减小1.5米
C. 增大3.5米 D. 减小3.5米课堂练习 3.如图:小明想测量电线杆AB的高度,发现电线杆的影子恰好落在土坡的坡面CD和地面CB上,测得CD=4m,BC=10m,CD与地面成30度角,且此时测得1米杆子的影子长为2米,那么电线杆的高度是多少?ABDC课堂练习课堂小结:一 、相似三角形的应用主要有如下两个方面
1 测高(不能直接使用皮尺或刻度尺量的)
2 测距(不能直接测量的两点间的距离)、测高的方法
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长的比例”的原理解决 、测距的方法
测量不能到达两点间的距离,常构造相似三角形求解小明在晚上由路灯A走向路灯B,当他走到P时,发现身后他的影子的顶部刚好接触路灯A的底部;当他再向前走12米到达Q时,发现身前他的影子的顶部刚好接触到路灯B的底部,已知小明的身高是1.6米,两个路灯高9.6米,且AP=QB=x米
(1)求两灯的距离
(2)当小明走到路灯B时,他在路灯A的影长为多少?(2006年茂名市)如图,李华晚上在路灯下散步.已知李华的身高AB=h,灯柱的高OP=O/P/=l,两灯柱之间的距离OO/=m.
(l)若李华距灯柱OP的水平距离OA=a,求他影子AC的长;
(2)若李华在两路灯之间行走,则他前后的两个影子的长度之和(DA+AC)是否是定值?请说明理由;
(3)若李华在点A朝着影子(如图箭头)的方向以匀速行走,试求他影子的顶端在地面上移动的速度. 努力现在,成就未来
