相似三角形的性质和判定[下学期]
文档属性
| 名称 | 相似三角形的性质和判定[下学期] |
|
|
| 格式 | rar | ||
| 文件大小 | 30.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-09-12 00:00:00 | ||
图片预览

文档简介
相似三角形的判定和性质(二)
班级 姓名
1. 填空题:
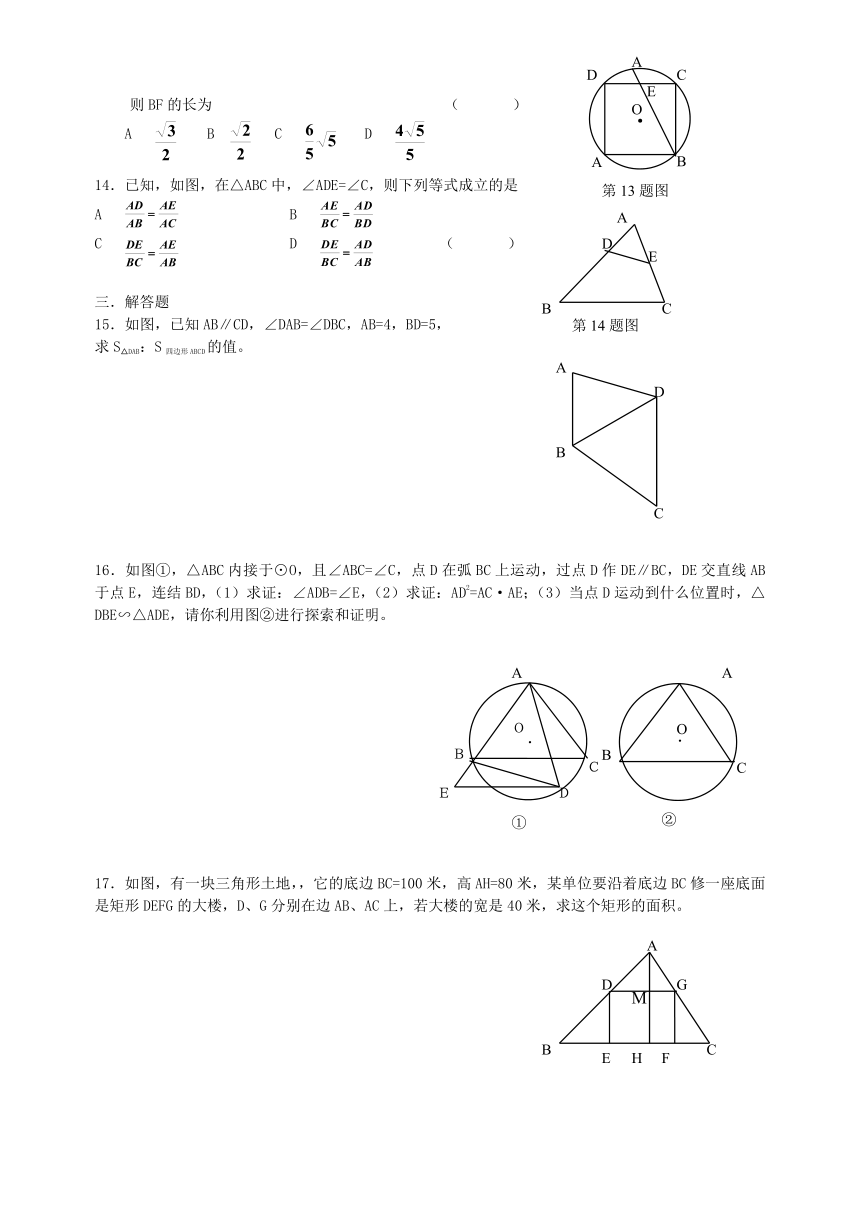
1. 如图是小明做的一个风筝的支架,AB=40cm,BP=60cm,且△ABC∽△APQ相似,则两者的相似比为 。
2.两个相似多边形最短边分别为15cm和6cm,它们的面积之差为630cm2,则它们的面积分别为 , 。
3.△ABC∽△A′B′C′,且AB=4,BC=5,AC=7,△A′B′C′的最大边为10.5,
则它们的相似比为 ,△A′B′C′的周长为 。
4.如图菱形BEFD内接于△ABC,且AB=18,AC=BC=12,那么菱形BEFD的周长是 。
5.如图,在Rt△ABC中,作出三个正方形,若第一个正方形的边长为9,第二个正方形的边长为6,则第三个正方形的面积为 。
6.在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AD=6,BD=2,则CD= ,BC= 。
7.△ABC中,D、E分别是AB、AC上点,且DE∥BC,S△ADE:S四边形BCED=1:2,
则AD:DB= 。
8.在△ABC中,D为AC边上的中点,AE∥BC,ED交AB于G,交BC的延长线于F,若BG:GA=3:1,BC=10,则AE的长为 。
2. 选择题:
9.如图,ABCD中,M是BC边上一点,且BM:MC=3:4,连接AM交BD于F,则BF:BD=
A 3:4 B 3:7 C 3:10 D 7:3 ( )
10.两个相似三角形的对应边上的中线的比是2:3,周长之和是20,那么这两个三角形的周长分别是
A 8和12 B 9和11 C 7和13 D 6和14 ( )
11.梯形ABCD的对角线交于点O,有以下四个结论:①△AOB∽△COD,②△AOD∽△ACB,③S△DOC:S△AOD
=DC:AB,④S△AOD=S△BOC 其中正确的有 ( )
A 1个 B 2个 C 3个 D 4个
12.如图,A、B、C、D、E、F、G、H、O都是5×7方格纸中的格点,为使△DME∽△ABC,则点M应是
F、G、H点中的 ( )
A. F B. G C. H D. O
13.如图,正方形ABCD内接于⊙O,E为DC的中点,直线BE交⊙O于点F,若⊙O的半径为 ,
则BF的长为 ( )
A B C D
14.已知,如图,在△ABC中,∠ADE=∠C,则下列等式成立的是
A B
C D ( )
三.解答题
15.如图,已知AB∥CD,∠DAB=∠DBC,AB=4,BD=5,
求S△DAB:S四边形ABCD的值。
16.如图①,△ABC内接于⊙O,且∠ABC=∠C,点D在弧BC上运动,过点D作DE∥BC,DE交直线AB于点E,连结BD,(1)求证:∠ADB=∠E,(2)求证:AD2=AC·AE;(3)当点D运动到什么位置时,△DBE∽△ADE,请你利用图②进行探索和证明。
17.如图,有一块三角形土地,,它的底边BC=100米,高AH=80米,某单位要沿着底边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上,若大楼的宽是40米,求这个矩形的面积。
18.在△ABC中,AB=AC=1,点D、E在直线BC上运动,设BD=x,CE=y,(1)如果
∠BAC=30°,∠DAE=105°,试确定y与x之间的函数关系式;(2)如果∠BAC=α,∠DAE=β,当α、β满足怎样的关系时,(1)中的y与x之间的函数关系式还成立?试说明理由。
19.已知:如图,在正方形ABCD中,AD=12,点E是边CD上的动点(点E不与端点C、D重合),AE的垂直平分线FP分别交AD、AE、BC于点F、H、G,交AB的延长线于点P,(1)设DE=m(020.在直角坐标系中,OM是第一象限的平分线,按以下要求解答问题:(1)将含45°角的三角板的直角顶点P在射线OM上移动,两直角边分别与Y轴,X轴交于点C、D,①在图甲中,证明:PC=PD;②在图乙中,点G是CD与OP的交点,且PG= PD,求△POD与△PDG的面积之比;(2)将三角板的直角顶点P在射线OM上移动,一直角边与X轴交于点D,OD=1,另一直角边与Y轴、X轴分别交于点C、E,使以P、D、E为顶点的三角形与△OCD相似,在图丙中画出图形,试求OP的长。
21.已知点P在线段AB上,点O在线段AB的延长线上,以点O为圆心,OP为半径作圆,点C是圆O的一点,(1)如图AP=2PB,PB=BO,求证:△CAO∽△BCO;(2)如果AP=m(m是常数且m>1),BP=1,OA:OP=OP:OB,当点C在圆O上运动时,求AC:BC的值(结果用含m的式子表示)
22.如图,AB是⊙O的直径,BC是⊙O的切线,OC平行于弦AD,DE⊥AB于E,AC交ED于P,求证:(1)△AED∽△OBC;(2) ;(3)EP=PD
23. 如图,有一边长为5cm的正方形ABCD和等腰三角形PQR,PQ=QR=5cm,QR=8cm,点B、C、Q、R在同一条直线l上,当C、Q两点重合时,等腰三角形PQR以1cm/秒的速度沿直线l按C至B的方向开始匀速运动,t秒后正方形ABCD与等腰△PQR重合部分的面积为Scm2。解答下列问题:(1)当t=3,求S的值;(2)当t=5时,求S的值;(3)当5≤t≤8时,求S与t之间的函数关系式。
A
C
D
O
B
第11题图
A
B
C
D
E
·
O
P
第1题图
Q
P
C
B
A
F
M
B
C
D
A
第9题图
A
G
C
F
H
E
B
D
M
B
C
E
F
P
R
T
A
S
Q
H
G
A
O
P
B
C
E
P
B
A
G
H
F
D
E
C
D
B
A
B
A
D
C
第4题图
B
C
F
E
D
A
第14题图
A
B
C
D
E
第7题图
B
F
G
C
D
E
A
第12题图
B
C
A
D
E
·
·
F
G
H
O
·
·
l
R
P
C
Q
B
D
A
第13题图
A
B
C
第5题图
甲
乙
M
X
D
O
P
C
X
O
丙
M
Y
O
X
D
P
C
Y
G
M
Y
.
O
A
O
·
D
E
A
C
B
D
E
.
O
B
C
A
②
①
班级 姓名
1. 填空题:
1. 如图是小明做的一个风筝的支架,AB=40cm,BP=60cm,且△ABC∽△APQ相似,则两者的相似比为 。
2.两个相似多边形最短边分别为15cm和6cm,它们的面积之差为630cm2,则它们的面积分别为 , 。
3.△ABC∽△A′B′C′,且AB=4,BC=5,AC=7,△A′B′C′的最大边为10.5,
则它们的相似比为 ,△A′B′C′的周长为 。
4.如图菱形BEFD内接于△ABC,且AB=18,AC=BC=12,那么菱形BEFD的周长是 。
5.如图,在Rt△ABC中,作出三个正方形,若第一个正方形的边长为9,第二个正方形的边长为6,则第三个正方形的面积为 。
6.在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AD=6,BD=2,则CD= ,BC= 。
7.△ABC中,D、E分别是AB、AC上点,且DE∥BC,S△ADE:S四边形BCED=1:2,
则AD:DB= 。
8.在△ABC中,D为AC边上的中点,AE∥BC,ED交AB于G,交BC的延长线于F,若BG:GA=3:1,BC=10,则AE的长为 。
2. 选择题:
9.如图,ABCD中,M是BC边上一点,且BM:MC=3:4,连接AM交BD于F,则BF:BD=
A 3:4 B 3:7 C 3:10 D 7:3 ( )
10.两个相似三角形的对应边上的中线的比是2:3,周长之和是20,那么这两个三角形的周长分别是
A 8和12 B 9和11 C 7和13 D 6和14 ( )
11.梯形ABCD的对角线交于点O,有以下四个结论:①△AOB∽△COD,②△AOD∽△ACB,③S△DOC:S△AOD
=DC:AB,④S△AOD=S△BOC 其中正确的有 ( )
A 1个 B 2个 C 3个 D 4个
12.如图,A、B、C、D、E、F、G、H、O都是5×7方格纸中的格点,为使△DME∽△ABC,则点M应是
F、G、H点中的 ( )
A. F B. G C. H D. O
13.如图,正方形ABCD内接于⊙O,E为DC的中点,直线BE交⊙O于点F,若⊙O的半径为 ,
则BF的长为 ( )
A B C D
14.已知,如图,在△ABC中,∠ADE=∠C,则下列等式成立的是
A B
C D ( )
三.解答题
15.如图,已知AB∥CD,∠DAB=∠DBC,AB=4,BD=5,
求S△DAB:S四边形ABCD的值。
16.如图①,△ABC内接于⊙O,且∠ABC=∠C,点D在弧BC上运动,过点D作DE∥BC,DE交直线AB于点E,连结BD,(1)求证:∠ADB=∠E,(2)求证:AD2=AC·AE;(3)当点D运动到什么位置时,△DBE∽△ADE,请你利用图②进行探索和证明。
17.如图,有一块三角形土地,,它的底边BC=100米,高AH=80米,某单位要沿着底边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上,若大楼的宽是40米,求这个矩形的面积。
18.在△ABC中,AB=AC=1,点D、E在直线BC上运动,设BD=x,CE=y,(1)如果
∠BAC=30°,∠DAE=105°,试确定y与x之间的函数关系式;(2)如果∠BAC=α,∠DAE=β,当α、β满足怎样的关系时,(1)中的y与x之间的函数关系式还成立?试说明理由。
19.已知:如图,在正方形ABCD中,AD=12,点E是边CD上的动点(点E不与端点C、D重合),AE的垂直平分线FP分别交AD、AE、BC于点F、H、G,交AB的延长线于点P,(1)设DE=m(0
21.已知点P在线段AB上,点O在线段AB的延长线上,以点O为圆心,OP为半径作圆,点C是圆O的一点,(1)如图AP=2PB,PB=BO,求证:△CAO∽△BCO;(2)如果AP=m(m是常数且m>1),BP=1,OA:OP=OP:OB,当点C在圆O上运动时,求AC:BC的值(结果用含m的式子表示)
22.如图,AB是⊙O的直径,BC是⊙O的切线,OC平行于弦AD,DE⊥AB于E,AC交ED于P,求证:(1)△AED∽△OBC;(2) ;(3)EP=PD
23. 如图,有一边长为5cm的正方形ABCD和等腰三角形PQR,PQ=QR=5cm,QR=8cm,点B、C、Q、R在同一条直线l上,当C、Q两点重合时,等腰三角形PQR以1cm/秒的速度沿直线l按C至B的方向开始匀速运动,t秒后正方形ABCD与等腰△PQR重合部分的面积为Scm2。解答下列问题:(1)当t=3,求S的值;(2)当t=5时,求S的值;(3)当5≤t≤8时,求S与t之间的函数关系式。
A
C
D
O
B
第11题图
A
B
C
D
E
·
O
P
第1题图
Q
P
C
B
A
F
M
B
C
D
A
第9题图
A
G
C
F
H
E
B
D
M
B
C
E
F
P
R
T
A
S
Q
H
G
A
O
P
B
C
E
P
B
A
G
H
F
D
E
C
D
B
A
B
A
D
C
第4题图
B
C
F
E
D
A
第14题图
A
B
C
D
E
第7题图
B
F
G
C
D
E
A
第12题图
B
C
A
D
E
·
·
F
G
H
O
·
·
l
R
P
C
Q
B
D
A
第13题图
A
B
C
第5题图
甲
乙
M
X
D
O
P
C
X
O
丙
M
Y
O
X
D
P
C
Y
G
M
Y
.
O
A
O
·
D
E
A
C
B
D
E
.
O
B
C
A
②
①
