相似三角形的判定定理[下学期]
文档属性
| 名称 | 相似三角形的判定定理[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 190.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-01-26 00:00:00 | ||
图片预览

文档简介
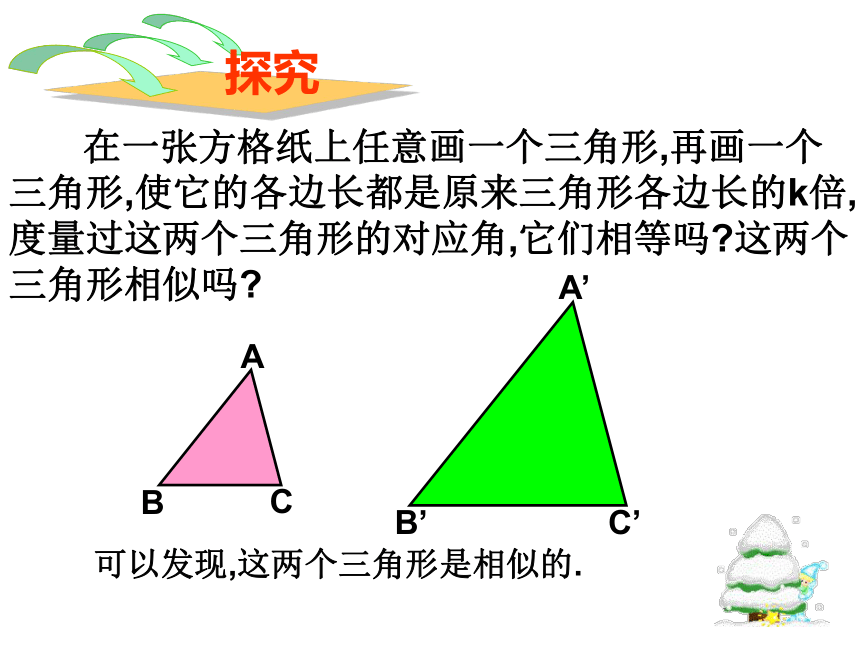
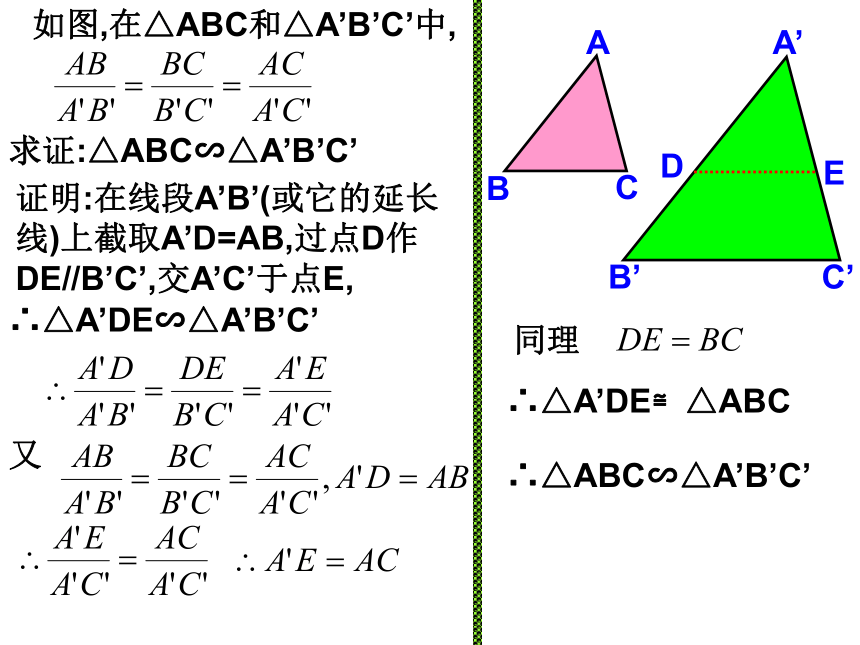
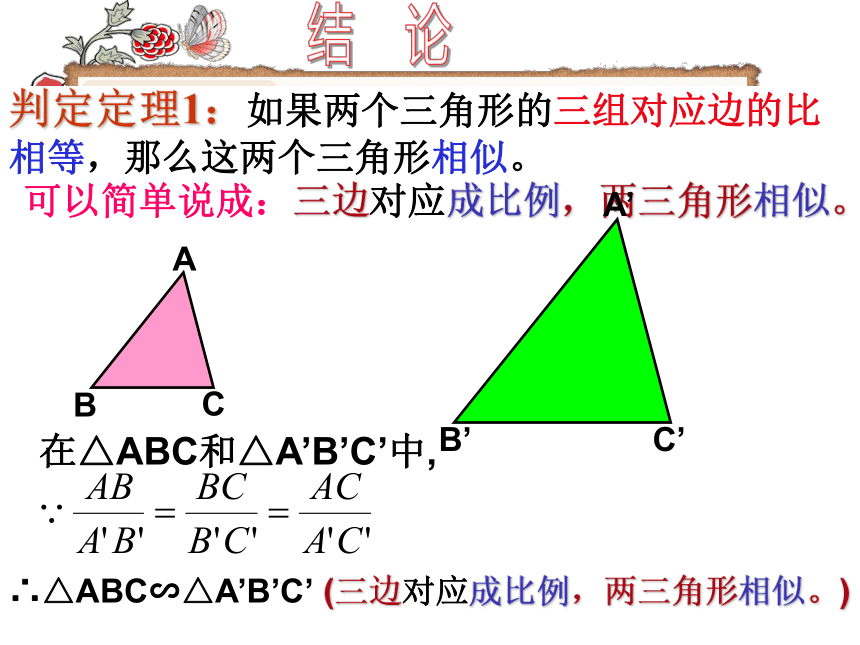
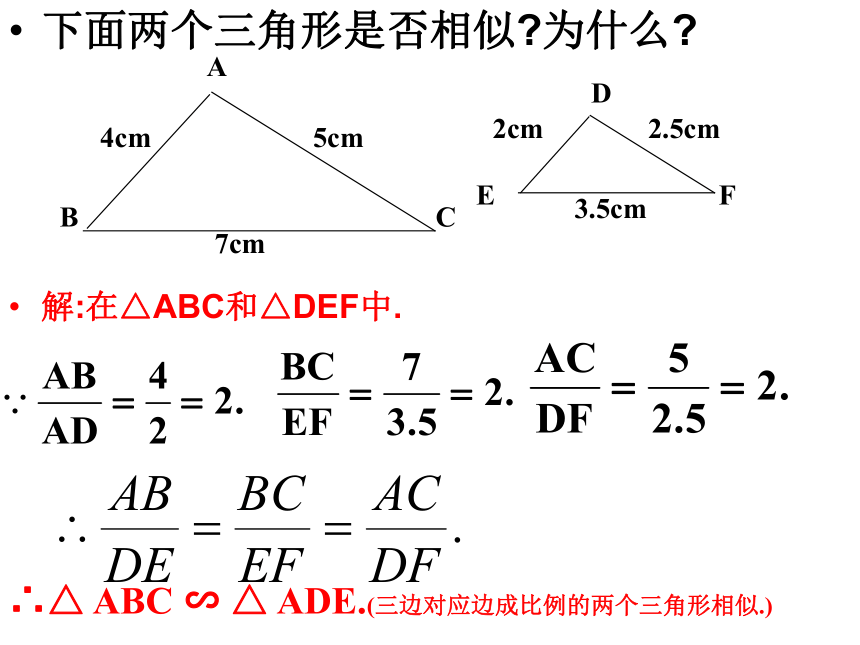
课件11张PPT。相似三角形的判定(第二课时) 在一张方格纸上任意画一个三角形,再画一个三角形,使它的各边长都是原来三角形各边长的k倍,度量过这两个三角形的对应角,它们相等吗?这两个三角形相似吗?可以发现,这两个三角形是相似的.如图,在△ABC和△A’B’C’中,求证:△ABC∽△A’B’C’证明:在线段A’B’(或它的延长线)上截取A’D=AB,过点D作DE//B’C’,交A’C’于点E,DE∴△A’DE∽△A’B’C’又同理∴△A’DE≌△ABC∴△ABC∽△A’B’C’判定定理1:如果两个三角形的三组对应边的比相等,那么这两个三角形相似。结 论可以简单说成:三边对应成比例,两三角形相似。在△ABC和△A’B’C’中,∴△ABC∽△A’B’C’(三边对应成比例,两三角形相似。)下面两个三角形是否相似?为什么?解:在△ABC和△DEF中.∴△ ABC ∽ △ ADE.(三边对应边成比例的两个三角形相似.)例 题 讲 解例1:如图,D,E,F分别是△ABC三边的中点,
求证:△EFD∽△ABC证明:∵D是AB的中点,F是AC的中点,∴BC=2DF同理∴△EFD∽△ABC(三边对应成比例,两三角形相似。)如图,△ ABC与△ A′B′C′相似吗?
你用什么方法来支持你的判断?
∴△ ABC∽△ A′B′C′ 解:如图,设小正方形的边长为1,由勾股定理可得:相似三角形判定方法1、三组对应边的比相等且对应角相等;2、平行于三角形一边的直线与其他两边(或 两边的延长线)相交,所构成的三角形与原三角形相似。总结反思 与同桌交流一下你这节课的收获! 3、三组对应边的比相等的两个三角形相似。牛刀小试: 根据下列条件判断△ABC与以D、E、F为顶点的两个三角形是否相似。(1)AB=3,BC=4,AC=6;
DE=6,EF=8,DF=12(3)AB=3,BC=4,AC=6;
DE=6,EF=9,DF=12(2)AB=3,BC=4,AC=6;
DE=6,EF=8,DF=12△ABC∽△DEF△ABC∽不 相 似△EDFDE=6,EF=12,DF=8△ABC∽△DEF例题教学:例2 如图,判断4×4方格中的两个三角形是否相似,并说明理由.例题教学:证明:即 ∠BAD=∠CAE∵∴△ABC∽△ADE∴∠BAC=∠DAE∴∠BAC-∠DAC =∠DAE-∠DAC
求证:△EFD∽△ABC证明:∵D是AB的中点,F是AC的中点,∴BC=2DF同理∴△EFD∽△ABC(三边对应成比例,两三角形相似。)如图,△ ABC与△ A′B′C′相似吗?
你用什么方法来支持你的判断?
∴△ ABC∽△ A′B′C′ 解:如图,设小正方形的边长为1,由勾股定理可得:相似三角形判定方法1、三组对应边的比相等且对应角相等;2、平行于三角形一边的直线与其他两边(或 两边的延长线)相交,所构成的三角形与原三角形相似。总结反思 与同桌交流一下你这节课的收获! 3、三组对应边的比相等的两个三角形相似。牛刀小试: 根据下列条件判断△ABC与以D、E、F为顶点的两个三角形是否相似。(1)AB=3,BC=4,AC=6;
DE=6,EF=8,DF=12(3)AB=3,BC=4,AC=6;
DE=6,EF=9,DF=12(2)AB=3,BC=4,AC=6;
DE=6,EF=8,DF=12△ABC∽△DEF△ABC∽不 相 似△EDFDE=6,EF=12,DF=8△ABC∽△DEF例题教学:例2 如图,判断4×4方格中的两个三角形是否相似,并说明理由.例题教学:证明:即 ∠BAD=∠CAE∵∴△ABC∽△ADE∴∠BAC=∠DAE∴∠BAC-∠DAC =∠DAE-∠DAC
