2007年相似三角形的举例应用(第二课时)[上学期] 新人教版[下学期]
文档属性
| 名称 | 2007年相似三角形的举例应用(第二课时)[上学期] 新人教版[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 288.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-01-26 00:00:00 | ||
图片预览


文档简介
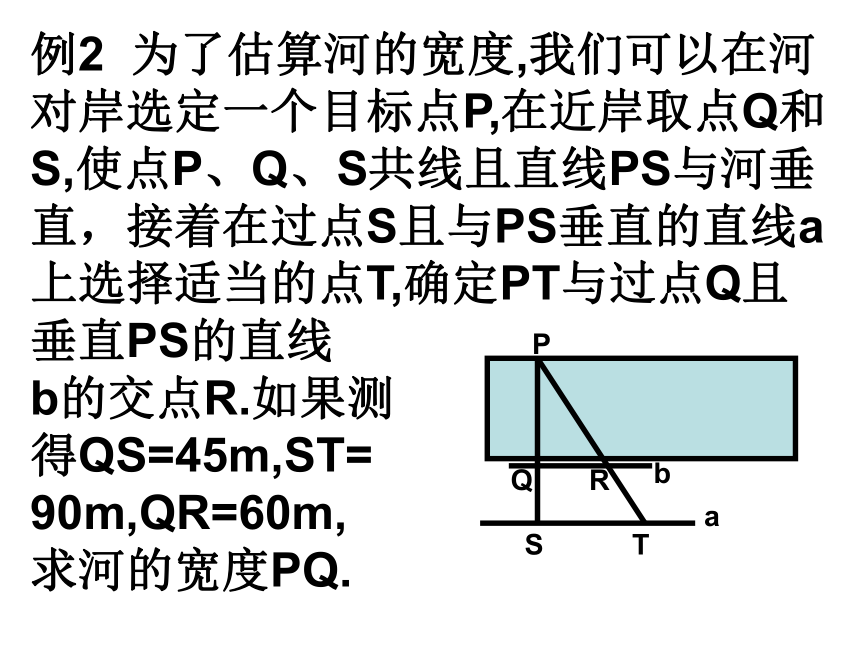
课件9张PPT。27.2.2相似三角形应用举例(二)上节课我们学习了利用相似三角形测量一些不能直接测量的物体的高度.回顾这节课我们学习利用相似三角形测量一些不能直接测量的物体的宽度.例2 为了估算河的宽度,我们可以在河对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线
b的交点R.如果测
得QS=45m,ST=
90m,QR=60m,
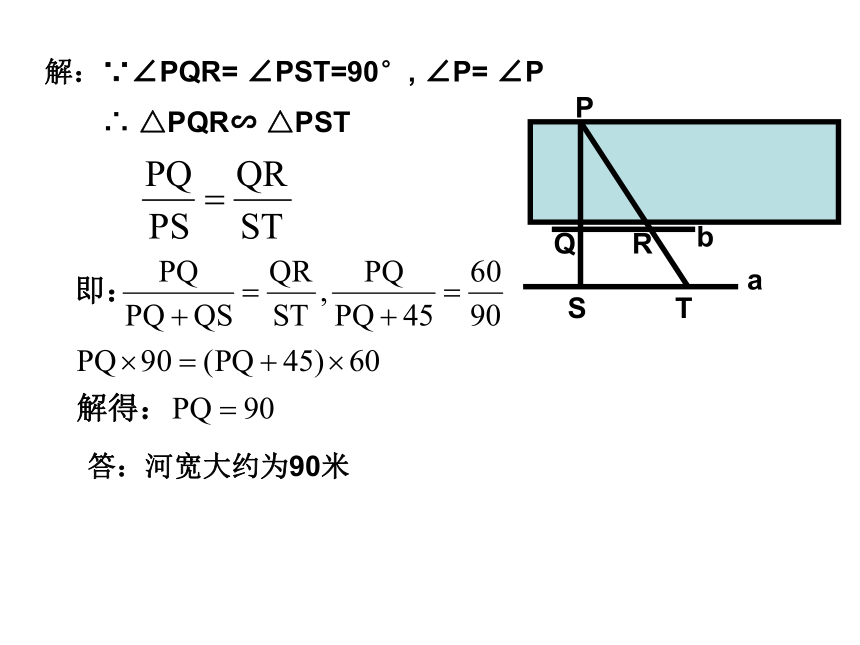
求河的宽度PQ.解:∵∠PQR= ∠PST=90°, ∠P= ∠P∴ △PQR∽ △PST答:河宽大约为90米 例3.已知左、右并排的两棵大树的高分别是AB=8m和CD=12m,两树的根部的距离BD=5m.一个身高1.6m的人沿着正对这两棵树的一条水平直路L从左向右前进,当他与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点C?解:如图:假设观察者从左向右走到点E时,
他的眼睛的位置点F与两棵树的顶端的点A、C
恰好在同一条直线上∴AB∥CD, △AHF∽ △CFK由题意可知,AB⊥FG, CD⊥FG由此可知,如果观察者继续前进,即他与左边的树的距离小于
8米时,由于这棵树的遮挡,右边树的顶端点C在观察者的盲区
内,观察者看不到它。练习:P51练习2大家都来动动手挑战自我 如图,△ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?NMQPEDCBA解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。
因为PN∥BC,所以△APN∽ △ABC
所以
他的眼睛的位置点F与两棵树的顶端的点A、C
恰好在同一条直线上∴AB∥CD, △AHF∽ △CFK由题意可知,AB⊥FG, CD⊥FG由此可知,如果观察者继续前进,即他与左边的树的距离小于
8米时,由于这棵树的遮挡,右边树的顶端点C在观察者的盲区
内,观察者看不到它。练习:P51练习2大家都来动动手挑战自我 如图,△ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?NMQPEDCBA解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。
因为PN∥BC,所以△APN∽ △ABC
所以
