青岛市2013-2014学年第一学期九年级数学期中考试题(有答案)
文档属性
| 名称 | 青岛市2013-2014学年第一学期九年级数学期中考试题(有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 107.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-02 00:00:00 | ||
图片预览

文档简介
青岛市2013——2014学年度第一学期九年级数学期中考试题
(时间 90分钟 满分 120分)
题号 一 二 三 四 合计 合计人 复核人
15 16 17 18 19 20 21 22 23 24
得分
一、选择题(本题满分24分,共有8道小题,每小题3分)
下列每小题都给出标号为A、B、C、D的四个结论,其中只有一个是正确的.每小题选对得分;不选、选错或选出的标号超过一个的不得分.请将1—8各小题所选答案的标号填写在第8小题后面的表格内.
1、已知三角形两边长分别为2和9,第三边的长为二次方程x2-14x+48=0的一根,
则这个三角形的周长为( )
A.11 B.17 C.17或19 D.19
2、下列方程中,是关于x的一元二次方程的是( )
A、 B、
C、 D、
3、元旦期间,一个小组有若干人,他们之间互送贺卡一张,已知全组共送贺卡132张,则这个小组共有( )人
A、11 B、12 C、13 D、14
4、顺次连接某个四边形各边中点得到一个正方形,则原四边形一定是( )
A、正方形 B、对角线互相垂直的等腰梯形
C、菱形 D、对角线互相垂直且相等的四边形
5、正方形具有而菱形不一定具有的性质是( )
A、对角线互相平分 B、对角线相等 C、对角线平分一组对角 D、对角线互相垂直
6、小丽要在一幅长为80cm,宽为50cm的矩形风景画的四周外围镶上一条宽度相同的金
色纸边制成一幅矩形挂图,使整幅挂图的面积是5400,设金色纸边的宽度为xcm,
则x满足的方程是( )
A、 B、
C、 D、
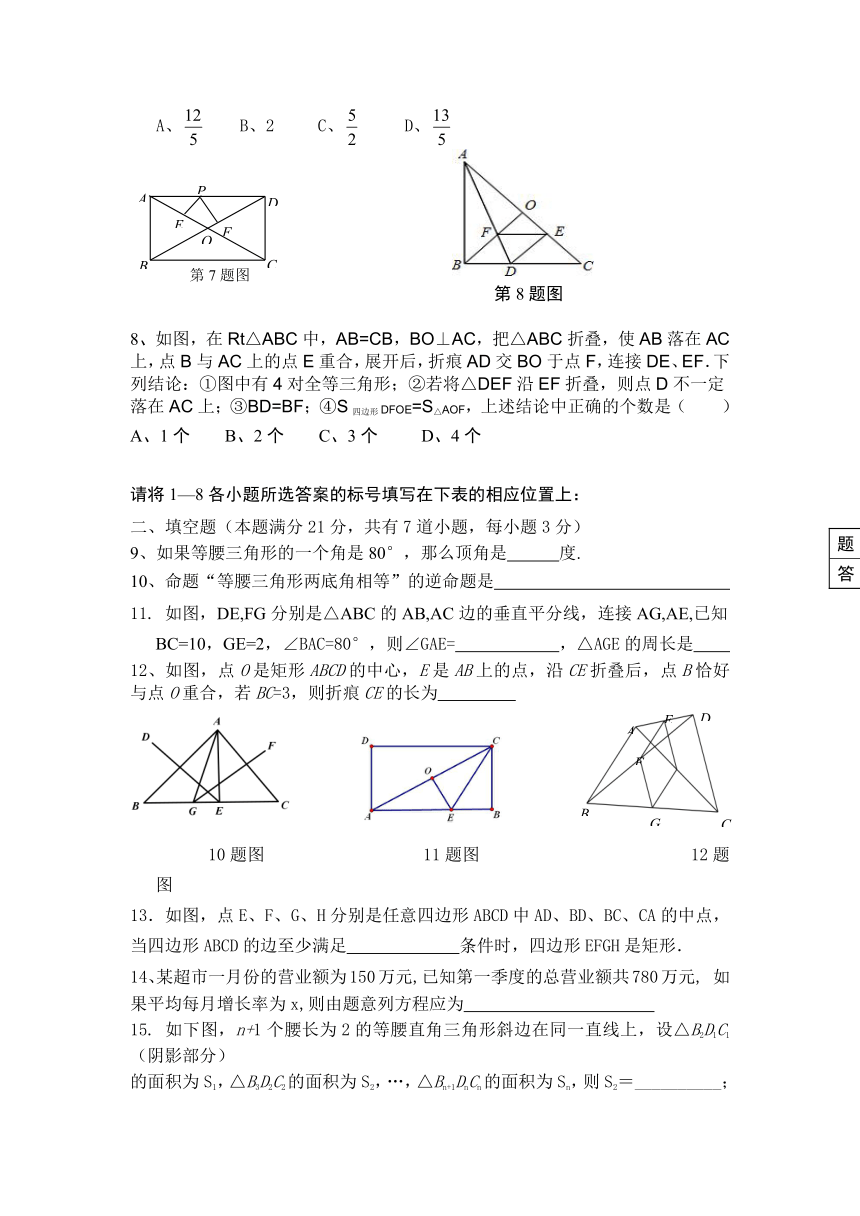
7、如图2,在矩形ABCD中,AB=3,AD=4,P是AD上的动点,PE⊥AC于E,PF⊥BD于F,则PE+FF的值是( )
A、 B、2 C、 D、
第8题图
8、如图,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AD交BO于点F,连接DE、EF.下列结论:①图中有4对全等三角形;②若将△DEF沿EF折叠,则点D不一定落在AC上;③BD=BF;④S四边形DFOE=S△AOF,上述结论中正确的个数是( )
A、1个 B、2个 C、3个 D、4个
请将1—8各小题所选答案的标号填写在下表的相应位置上:
题 号 1 2 3 4 5 6 7 8
答 案
二、填空题(本题满分21分,共有7道小题,每小题3分)
9、如果等腰三角形的一个角是80°,那么顶角是 度.
10、命题“等腰三角形两底角相等”的逆命题是
11. 如图,DE,FG分别是△ABC的AB,AC边的垂直平分线,连接AG,AE,已知BC=10,GE=2,∠BAC=80°,则∠GAE= ,△AGE的周长是
12、如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为
10题图 11题图 12题图
13.如图,点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,当四边形ABCD的边至少满足 条件时,四边形EFGH是矩形.
14、某超市一月份的营业额为150万元,已知第一季度的总营业额共780万元, 如果平均每月增长率为x,则由题意列方程应为
15. 如下图,n+1个腰长为2的等腰直角三角形斜边在同一直线上,设△B2D1C1(阴影部分)
的面积为S1,△B3D2C2的面积为S2,…,△Bn+1DnCn的面积为Sn,则S2=__________;Sn=__________.(用含n的式子表示).
请将9—14各小题的答案填写在下表中相应的位置上:
题 号 9 10 11 12
答 案
题 号 13 14 15
答 案
三、解答题
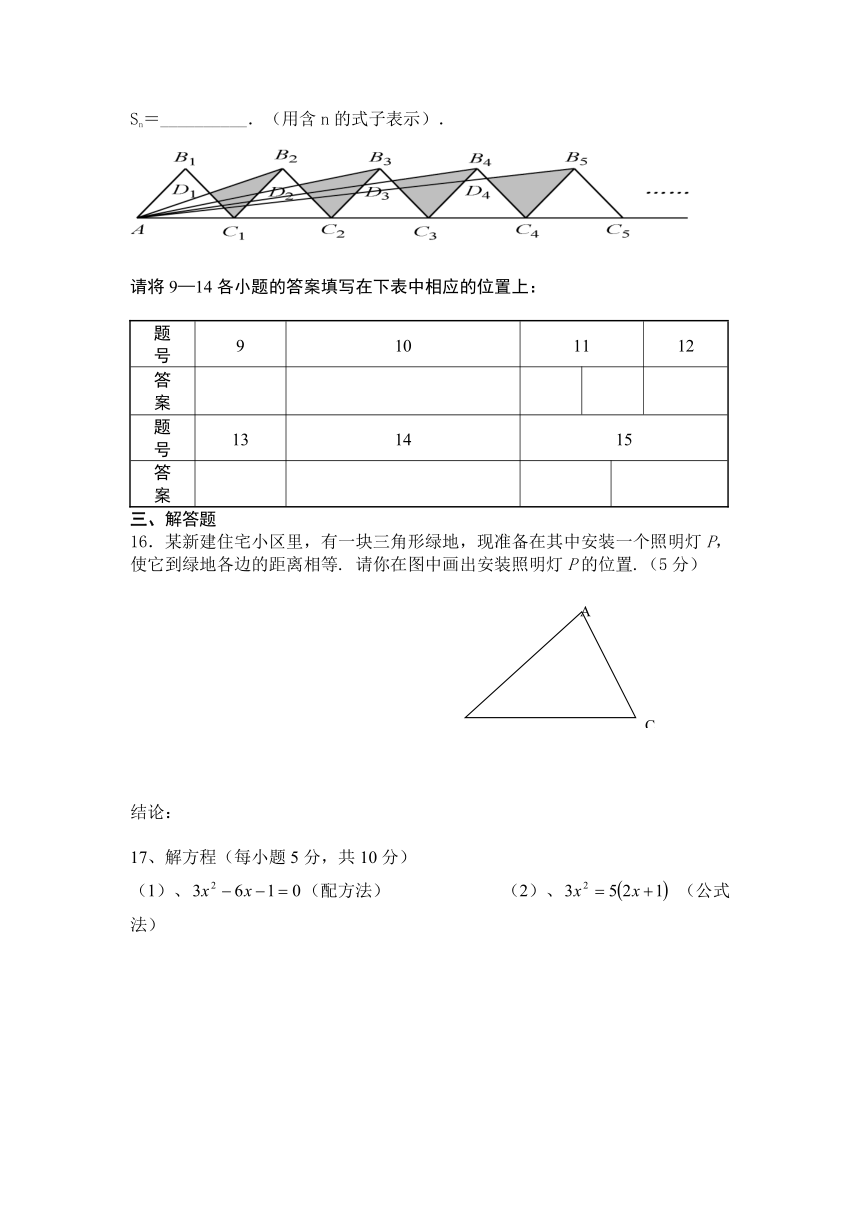
16.某新建住宅小区里,有一块三角形绿地,现准备在其中安装一个照明灯P,使它到绿地各边的距离相等. 请你在图中画出安装照明灯P的位置.(5分)
结论:
17、解方程(每小题5分,共10分)
(1)、(配方法) (2)、 (公式法)
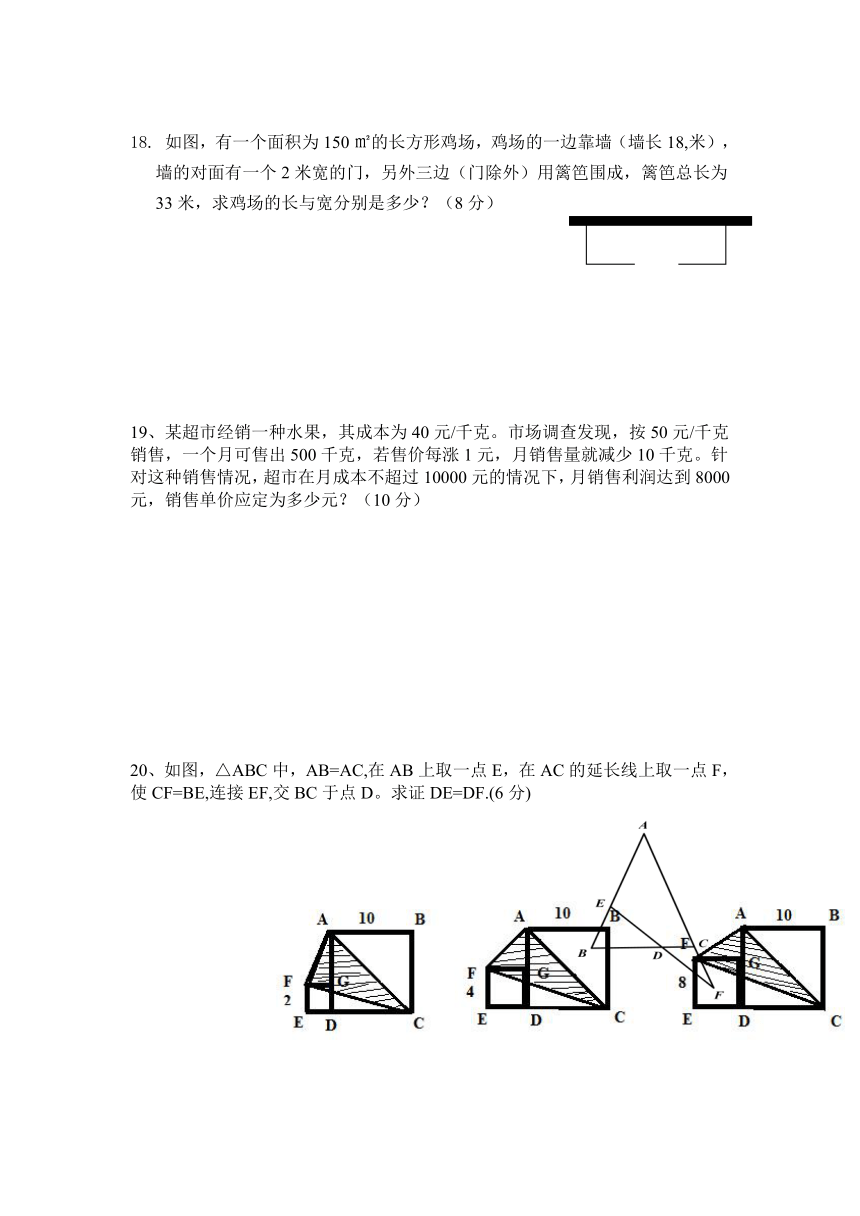
18. 如图,有一个面积为150㎡的长方形鸡场,鸡场的一边靠墙(墙长18,米),墙的对面有一个2米宽的门,另外三边(门除外)用篱笆围成,篱笆总长为33米,求鸡场的长与宽分别是多少?(8分)
19、某超市经销一种水果,其成本为40元/千克。市场调查发现,按50元/千克销售,一个月可售出500千克,若售价每涨1元,月销售量就减少10千克。针对这种销售情况,超市在月成本不超过10000元的情况下,月销售利润达到8000元,销售单价应定为多少元?(10分)
20、如图,△ABC中,AB=AC,在AB上取一点E,在AC的延长线上取一点F,
使CF=BE,连接EF,交BC于点D。求证DE=DF.(6分)
21、如图,在□ABDC中,分别取AC、BD的中点E和F,连接BE、CF,过点A作
AP∥BC,交DC的延长线于点P.(10分)
(1)求证:△ABE≌△DCF;
(2)当∠P满足什么条件时,四边形BECF是菱形?证明你的结论.
证明:(1)
(2)
22、
【探究发现】(5分)
按图中方式将大小不同的两个正方形放在一起,分别求出阴影部分(⊿ACF)的面积。(单位:厘米,阴影部分的面积依次用S1、S2、S3表示)
1.S1= cm2; S2= cm2; S3= cm2.
2.归纳总结你的发现:
【推理反思】(4分)
按图中方式将大小不同的两个正方形放在一起,设小正方形的边长是b cm ,大正方形的边长是a cm,求:阴影部分(⊿ACF)的面积。
【应用拓展】(5分)
1.按上图方式将大小不同的两个正方形放在一起,若大正方形的面积是80cm2,则图中阴影三角形的面积是 cm2.
2.如图(1),C是线段AB上任意一点,分别以AC、BC为边在线段AB同侧构造等边三角形⊿ACD和等边三角形⊿CBE,若⊿CBE的边长是1 cm,则图中阴影三角形的面积
是 cm2.
3. 如图(2),菱形ABCD和菱形ECGF的边长分别为2和3,∠A=120°,则图中阴影部分的面积是
(1) (2)
22.(本小题满分12分)
如图1,已知△ABC中,AB=10cm,AC=8cm,BC=6cm.如果点P由B出发沿BA方向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
(1)当t为何值时,PQ∥BC.
(2)设△AQP面积为S(单位:cm2),求S与t的函数关系式
(3)是否存在某时刻t,使四边形BPQC的面积为△ABC面积的三分之二?若存在,求出此时t的值;若不存在,请说明理由.
(4)如图2,把△AQP沿AP翻折,得到四边形AQPQ′.那么是否存在某时刻t,使四边形AQPQ′为菱形?
答案
请将1—8各小题所选答案的标号填写在下表的相应位置上:
题 号 1 2 3 4 5 6 7 8
答 案 D B B D B C A C
请将9—14各小题的答案填写在下表中相应的位置上:
题 号 9 10 11 12
答 案 80°或20° 有两个角相等的三角形是等腰三角形 20° 14 2
题 号 13 14 15
答 案 AB⊥CD 1
16、每条角平分线2分,结论1分
17、(1)解:--------------1分
-------------3分
-----------4分
---5分
(2)、----------------1分
b=-10 c=-5-------------2分
--3分
--------------------4分
-----5分
18、解:设垂直于墙的一边长为x米,由题意得
-----------------------3分
解得 ---------------------5分
当x=时,33-2x+2=20>18 ∵x=不合题意,舍去-----6分
当x=10时,33-2x+2=15----------------------------7分
答:养鸡场的长为15米,宽为10米-------------------8分
19、解:设销售单价为x元,由题意得:
-----------------4分
解得 -----------------------7分
∵----------------8分
∴不合题意,舍去------------------9分
答:销售单价应定为80元.--------------------------10分
20、6分
21、每小题5分
22、【探究发现】1.50 50 50 每空1分 2. (3分) 【推理反思】(4分)
【应用拓展】1.40 -------1分2. -----2分 3.--------2分
23、 (1)、--------3分(2)、------3分
(3)、= = 方程无解,不存在—3分
(4)、---------------3分
F
O
P
E
D
C
B
A
第7题图
A
B
C
D
E
F
G
A
C
A
B
D
F
C
P
E
(时间 90分钟 满分 120分)
题号 一 二 三 四 合计 合计人 复核人
15 16 17 18 19 20 21 22 23 24
得分
一、选择题(本题满分24分,共有8道小题,每小题3分)
下列每小题都给出标号为A、B、C、D的四个结论,其中只有一个是正确的.每小题选对得分;不选、选错或选出的标号超过一个的不得分.请将1—8各小题所选答案的标号填写在第8小题后面的表格内.
1、已知三角形两边长分别为2和9,第三边的长为二次方程x2-14x+48=0的一根,
则这个三角形的周长为( )
A.11 B.17 C.17或19 D.19
2、下列方程中,是关于x的一元二次方程的是( )
A、 B、
C、 D、
3、元旦期间,一个小组有若干人,他们之间互送贺卡一张,已知全组共送贺卡132张,则这个小组共有( )人
A、11 B、12 C、13 D、14
4、顺次连接某个四边形各边中点得到一个正方形,则原四边形一定是( )
A、正方形 B、对角线互相垂直的等腰梯形
C、菱形 D、对角线互相垂直且相等的四边形
5、正方形具有而菱形不一定具有的性质是( )
A、对角线互相平分 B、对角线相等 C、对角线平分一组对角 D、对角线互相垂直
6、小丽要在一幅长为80cm,宽为50cm的矩形风景画的四周外围镶上一条宽度相同的金
色纸边制成一幅矩形挂图,使整幅挂图的面积是5400,设金色纸边的宽度为xcm,
则x满足的方程是( )
A、 B、
C、 D、
7、如图2,在矩形ABCD中,AB=3,AD=4,P是AD上的动点,PE⊥AC于E,PF⊥BD于F,则PE+FF的值是( )
A、 B、2 C、 D、
第8题图
8、如图,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AD交BO于点F,连接DE、EF.下列结论:①图中有4对全等三角形;②若将△DEF沿EF折叠,则点D不一定落在AC上;③BD=BF;④S四边形DFOE=S△AOF,上述结论中正确的个数是( )
A、1个 B、2个 C、3个 D、4个
请将1—8各小题所选答案的标号填写在下表的相应位置上:
题 号 1 2 3 4 5 6 7 8
答 案
二、填空题(本题满分21分,共有7道小题,每小题3分)
9、如果等腰三角形的一个角是80°,那么顶角是 度.
10、命题“等腰三角形两底角相等”的逆命题是
11. 如图,DE,FG分别是△ABC的AB,AC边的垂直平分线,连接AG,AE,已知BC=10,GE=2,∠BAC=80°,则∠GAE= ,△AGE的周长是
12、如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为
10题图 11题图 12题图
13.如图,点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,当四边形ABCD的边至少满足 条件时,四边形EFGH是矩形.
14、某超市一月份的营业额为150万元,已知第一季度的总营业额共780万元, 如果平均每月增长率为x,则由题意列方程应为
15. 如下图,n+1个腰长为2的等腰直角三角形斜边在同一直线上,设△B2D1C1(阴影部分)
的面积为S1,△B3D2C2的面积为S2,…,△Bn+1DnCn的面积为Sn,则S2=__________;Sn=__________.(用含n的式子表示).
请将9—14各小题的答案填写在下表中相应的位置上:
题 号 9 10 11 12
答 案
题 号 13 14 15
答 案
三、解答题
16.某新建住宅小区里,有一块三角形绿地,现准备在其中安装一个照明灯P,使它到绿地各边的距离相等. 请你在图中画出安装照明灯P的位置.(5分)
结论:
17、解方程(每小题5分,共10分)
(1)、(配方法) (2)、 (公式法)
18. 如图,有一个面积为150㎡的长方形鸡场,鸡场的一边靠墙(墙长18,米),墙的对面有一个2米宽的门,另外三边(门除外)用篱笆围成,篱笆总长为33米,求鸡场的长与宽分别是多少?(8分)
19、某超市经销一种水果,其成本为40元/千克。市场调查发现,按50元/千克销售,一个月可售出500千克,若售价每涨1元,月销售量就减少10千克。针对这种销售情况,超市在月成本不超过10000元的情况下,月销售利润达到8000元,销售单价应定为多少元?(10分)
20、如图,△ABC中,AB=AC,在AB上取一点E,在AC的延长线上取一点F,
使CF=BE,连接EF,交BC于点D。求证DE=DF.(6分)
21、如图,在□ABDC中,分别取AC、BD的中点E和F,连接BE、CF,过点A作
AP∥BC,交DC的延长线于点P.(10分)
(1)求证:△ABE≌△DCF;
(2)当∠P满足什么条件时,四边形BECF是菱形?证明你的结论.
证明:(1)
(2)
22、
【探究发现】(5分)
按图中方式将大小不同的两个正方形放在一起,分别求出阴影部分(⊿ACF)的面积。(单位:厘米,阴影部分的面积依次用S1、S2、S3表示)
1.S1= cm2; S2= cm2; S3= cm2.
2.归纳总结你的发现:
【推理反思】(4分)
按图中方式将大小不同的两个正方形放在一起,设小正方形的边长是b cm ,大正方形的边长是a cm,求:阴影部分(⊿ACF)的面积。
【应用拓展】(5分)
1.按上图方式将大小不同的两个正方形放在一起,若大正方形的面积是80cm2,则图中阴影三角形的面积是 cm2.
2.如图(1),C是线段AB上任意一点,分别以AC、BC为边在线段AB同侧构造等边三角形⊿ACD和等边三角形⊿CBE,若⊿CBE的边长是1 cm,则图中阴影三角形的面积
是 cm2.
3. 如图(2),菱形ABCD和菱形ECGF的边长分别为2和3,∠A=120°,则图中阴影部分的面积是
(1) (2)
22.(本小题满分12分)
如图1,已知△ABC中,AB=10cm,AC=8cm,BC=6cm.如果点P由B出发沿BA方向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
(1)当t为何值时,PQ∥BC.
(2)设△AQP面积为S(单位:cm2),求S与t的函数关系式
(3)是否存在某时刻t,使四边形BPQC的面积为△ABC面积的三分之二?若存在,求出此时t的值;若不存在,请说明理由.
(4)如图2,把△AQP沿AP翻折,得到四边形AQPQ′.那么是否存在某时刻t,使四边形AQPQ′为菱形?
答案
请将1—8各小题所选答案的标号填写在下表的相应位置上:
题 号 1 2 3 4 5 6 7 8
答 案 D B B D B C A C
请将9—14各小题的答案填写在下表中相应的位置上:
题 号 9 10 11 12
答 案 80°或20° 有两个角相等的三角形是等腰三角形 20° 14 2
题 号 13 14 15
答 案 AB⊥CD 1
16、每条角平分线2分,结论1分
17、(1)解:--------------1分
-------------3分
-----------4分
---5分
(2)、----------------1分
b=-10 c=-5-------------2分
--3分
--------------------4分
-----5分
18、解:设垂直于墙的一边长为x米,由题意得
-----------------------3分
解得 ---------------------5分
当x=时,33-2x+2=20>18 ∵x=不合题意,舍去-----6分
当x=10时,33-2x+2=15----------------------------7分
答:养鸡场的长为15米,宽为10米-------------------8分
19、解:设销售单价为x元,由题意得:
-----------------4分
解得 -----------------------7分
∵----------------8分
∴不合题意,舍去------------------9分
答:销售单价应定为80元.--------------------------10分
20、6分
21、每小题5分
22、【探究发现】1.50 50 50 每空1分 2. (3分) 【推理反思】(4分)
【应用拓展】1.40 -------1分2. -----2分 3.--------2分
23、 (1)、--------3分(2)、------3分
(3)、= = 方程无解,不存在—3分
(4)、---------------3分
F
O
P
E
D
C
B
A
第7题图
A
B
C
D
E
F
G
A
C
A
B
D
F
C
P
E
同课章节目录
