相似三角形的判定(1)[下学期]
文档属性
| 名称 | 相似三角形的判定(1)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 75.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-03-12 20:32:00 | ||
图片预览

文档简介
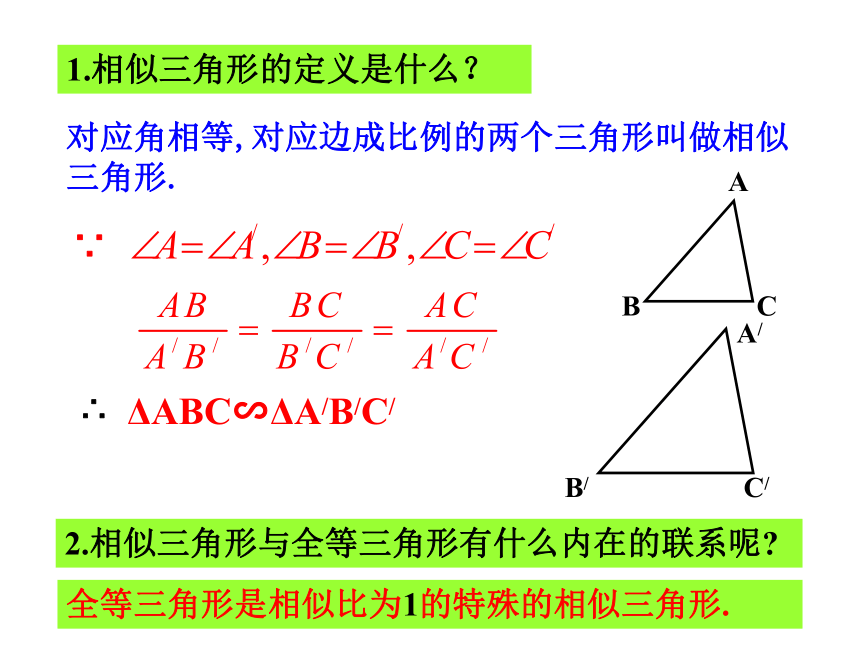
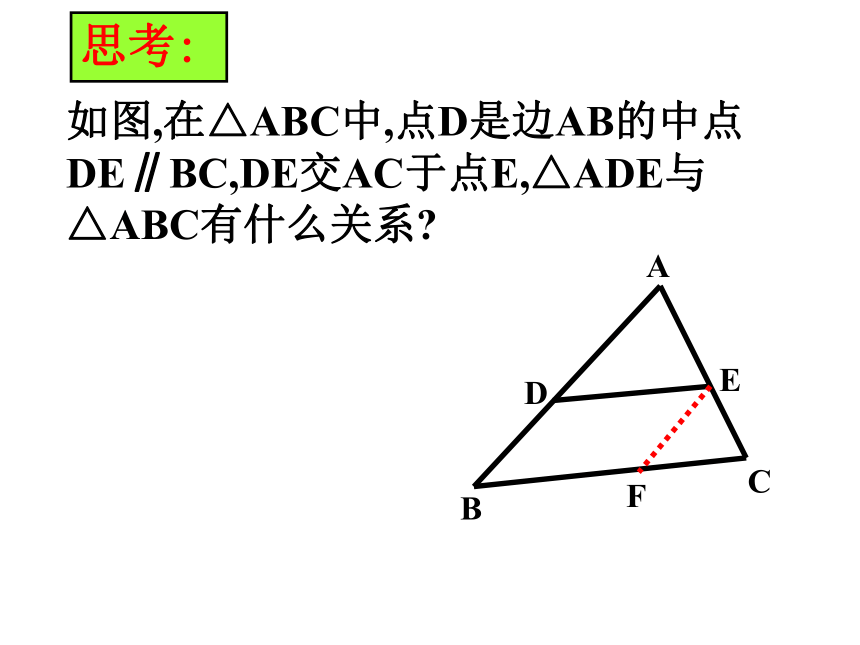
课件13张PPT。相似三角形的判定预备定理对应角相等,对应边成比例的两个三角形叫做相似三角形.1.相似三角形的定义是什么? ∵∴ΔABC∽ΔA/B/C/ 2.相似三角形与全等三角形有什么内在的联系呢?全等三角形是相似比为1的特殊的相似三角形.思考:如图,在△ABC中,点D是边AB的中点DE∥BC,DE交AC于点E,△ADE与△ABC有什么关系?ABCDEF如图在△ABC中,点D,E分别在AB,AC上,且DE∥BC,则△ADE与△ABC相似吗?
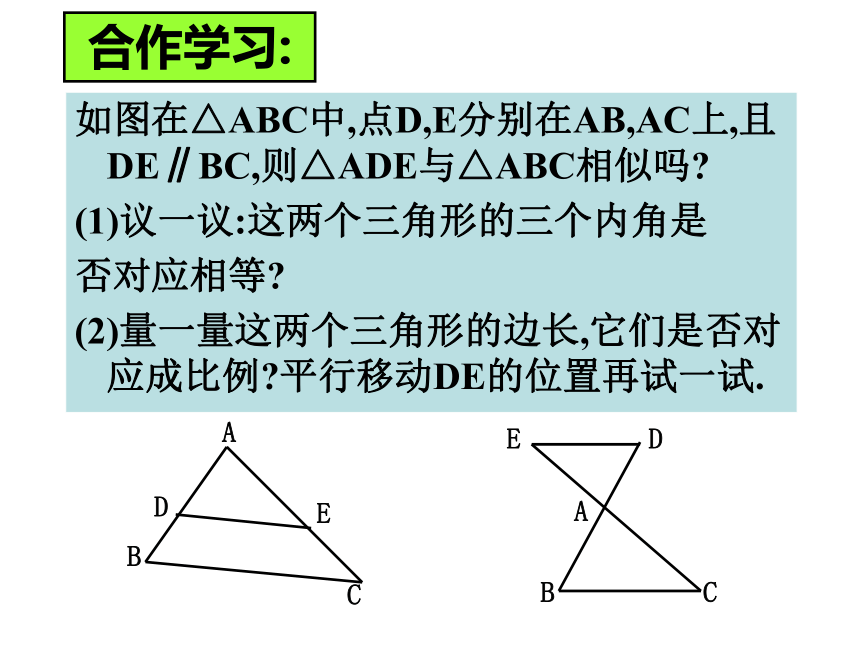
(1)议一议:这两个三角形的三个内角是
否对应相等?
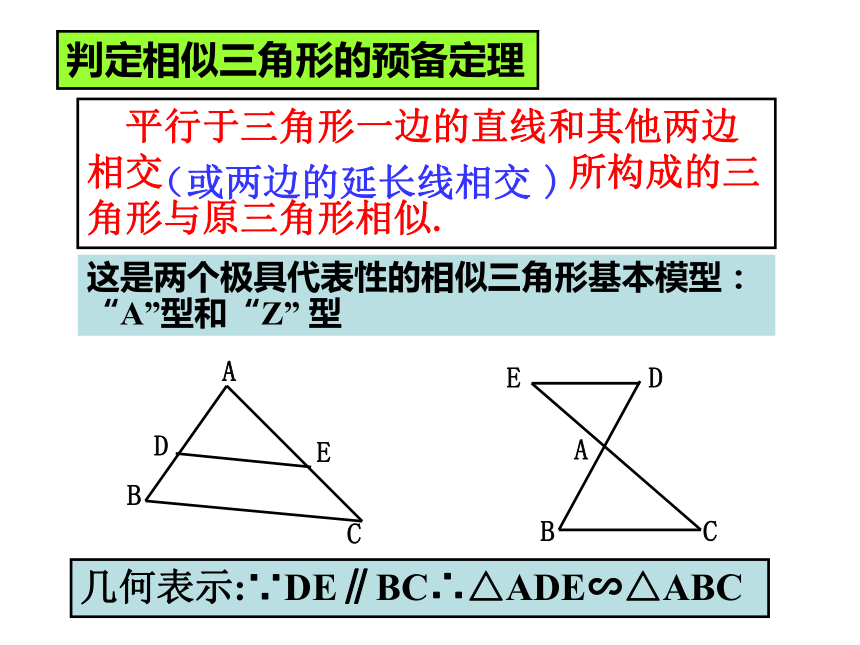
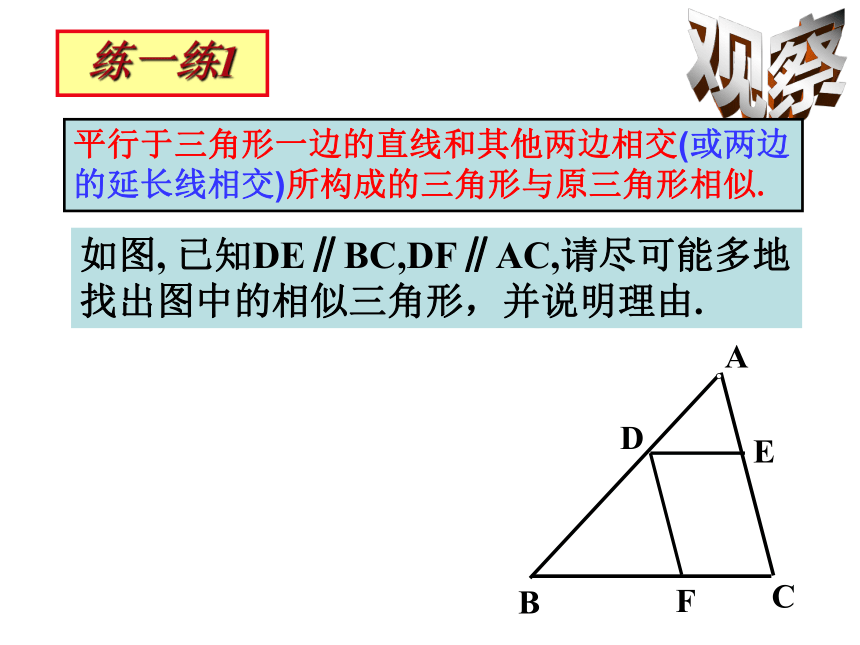
(2)量一量这两个三角形的边长,它们是否对应成比例?平行移动DE的位置再试一试.合作学习:D 平行于三角形一边的直线和其他两边相交 所构成的三角形与原三角形相似.(或两边的延长线相交 ) 这是两个极具代表性的相似三角形基本模型:“A”型和“Z” 型判定相似三角形的预备定理D几何表示:∵DE∥BC∴△ADE∽△ABC观察如图, 已知DE∥BC,DF∥AC,请尽可能多地找出图中的相似三角形,并说明理由.练一练1平行于三角形一边的直线和其他两边相交(或两边的延长线相交)所构成的三角形与原三角形相似.探究1已知:在△AB C和△A/B/ C/中求证:△ABC∽△A/B/C/判定定理1:如果二个三角形的三组边应边的比相等,那么这两个三角形相似.
简单说:三边对应成比例的两个三角形相似.′′′判定定理1的几何格式:∴△A′B′C′∽△ABC′′BCA例1根据下列条件,判断△ABC和△A1B1C1是否相似,并说明理由
AB=4cm BC=6cm AC=8cm
A1B1=12cm B1C1=18cm A1C1=21cm例2 如图判断4×4方格中的两个三角形是
否相似,并说明理由.EDFBAC练一练2 平行于三角形一边的直线和其他两边相交 所构成的三角形与原三角形相似.(或两边的延长线相交 ) 这是两个极具代表性的相似三角形基本模型:“A”型和“Z” 型判定相似三角形的预备定理D几何表示:∵DE∥BC∴△ADE∽△ABC判定定理1:如果二个三角形的三组边应边的比相等,那么这两个三角形相似.
简单说:三边对应成比例的两个三角形相似.′′′判定定理1的几何格式:∴△A′B′C′∽△ABC′′BCA
(1)议一议:这两个三角形的三个内角是
否对应相等?
(2)量一量这两个三角形的边长,它们是否对应成比例?平行移动DE的位置再试一试.合作学习:D 平行于三角形一边的直线和其他两边相交 所构成的三角形与原三角形相似.(或两边的延长线相交 ) 这是两个极具代表性的相似三角形基本模型:“A”型和“Z” 型判定相似三角形的预备定理D几何表示:∵DE∥BC∴△ADE∽△ABC观察如图, 已知DE∥BC,DF∥AC,请尽可能多地找出图中的相似三角形,并说明理由.练一练1平行于三角形一边的直线和其他两边相交(或两边的延长线相交)所构成的三角形与原三角形相似.探究1已知:在△AB C和△A/B/ C/中求证:△ABC∽△A/B/C/判定定理1:如果二个三角形的三组边应边的比相等,那么这两个三角形相似.
简单说:三边对应成比例的两个三角形相似.′′′判定定理1的几何格式:∴△A′B′C′∽△ABC′′BCA例1根据下列条件,判断△ABC和△A1B1C1是否相似,并说明理由
AB=4cm BC=6cm AC=8cm
A1B1=12cm B1C1=18cm A1C1=21cm例2 如图判断4×4方格中的两个三角形是
否相似,并说明理由.EDFBAC练一练2 平行于三角形一边的直线和其他两边相交 所构成的三角形与原三角形相似.(或两边的延长线相交 ) 这是两个极具代表性的相似三角形基本模型:“A”型和“Z” 型判定相似三角形的预备定理D几何表示:∵DE∥BC∴△ADE∽△ABC判定定理1:如果二个三角形的三组边应边的比相等,那么这两个三角形相似.
简单说:三边对应成比例的两个三角形相似.′′′判定定理1的几何格式:∴△A′B′C′∽△ABC′′BCA
