【专项】人教版七年级数学上册 第四章 几何图形初步解答题专项练习(含解析)
文档属性
| 名称 | 【专项】人教版七年级数学上册 第四章 几何图形初步解答题专项练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 11:51:56 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
几何图形初步解答题专项练习
1.已知,∠AOD=160°,OB,OM,ON是∠AOD内的射线.
(1)如图1,若OM平分∠AOB,ON平分∠BOD,∠AOB=40°,则∠BON= °;
(2)如图2,若OM平分∠AOB,ON平分∠BOD,求∠MON的度数;
(3)如图3,OC是∠AOD内的射线,若∠BOC=20°,OM平分∠AOC,ON平分∠BOD,当射线OB在∠AOC内时,求∠MON的度数.
2.解答下列各题:
(1)图①,是一副三角尺(COD和AOB)在桌面上叠放成的图形,已知OB平分∠COD,则∠AOC度数是 ;
(2)如图②,点O在直线AB上.
①若∠1=40°,∠4=20°,则∠COE的度数是 .
②如果OD为任意射线,OC平分∠AOD,OE平分∠BOD,求∠COE的度数.
3.已知:如图,O是直线AB上的一点,∠COD=90°,OE平分∠BOC.
(1)若∠AOC=30°,求∠COE的度数;
(2)若∠AOC=α,求∠DOE的度数(用含α的代数式表示).
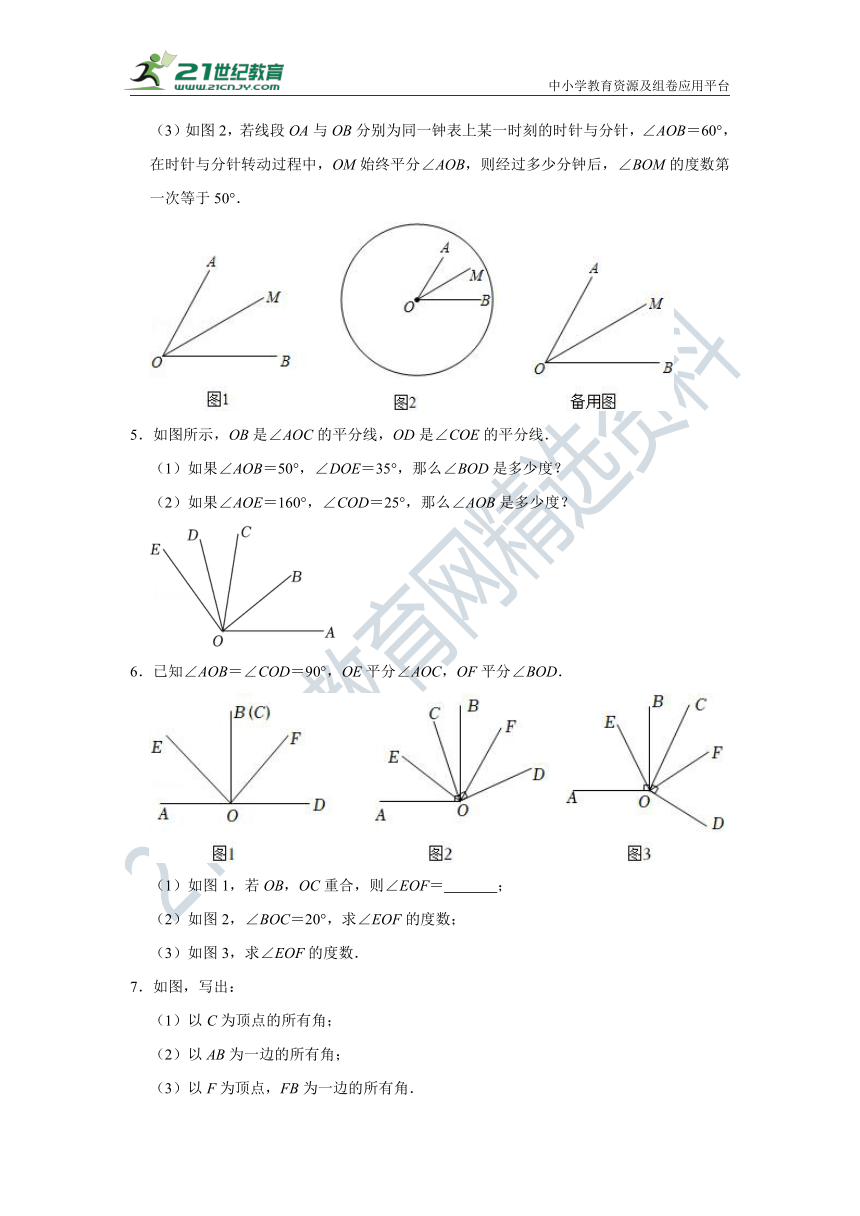
4.如图1,已知∠AOB=60°,OM平分∠AOB.
(1)∠BOM= ;
(2)若在图1中画射线OC,使得∠BOC=20°,ON平分∠BOC,求∠MON的大小;
(3)如图2,若线段OA与OB分别为同一钟表上某一时刻的时针与分针,∠AOB=60°,在时针与分针转动过程中,OM始终平分∠AOB,则经过多少分钟后,∠BOM的度数第一次等于50°.
5.如图所示,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)如果∠AOB=50°,∠DOE=35°,那么∠BOD是多少度?
(2)如果∠AOE=160°,∠COD=25°,那么∠AOB是多少度?
6.已知∠AOB=∠COD=90°,OE平分∠AOC,OF平分∠BOD.
(1)如图1,若OB,OC重合,则∠EOF= ;
(2)如图2,∠BOC=20°,求∠EOF的度数;
(3)如图3,求∠EOF的度数.
7.如图,写出:
(1)以C为顶点的所有角;
(2)以AB为一边的所有角;
(3)以F为顶点,FB为一边的所有角.
8.点O为直线AB上一点,将一直角三角板OMN的直角顶点放在点O处,射线OC平分∠MOB.
(1)如图1,若∠AOM=30°,求∠CON的度数;
(2)在图1中,若∠AOM=α,直接写出∠CON的度数(用含α的式子表示);
(3)将图1中的直角三角板OMN绕顶点O顺时针旋转至图2的位置,一边OM在直线AB上方,另一边ON在直线AB下方.
①探究∠AOM和∠CON的度数之间的关系,写出你的结论,并说明理由;
②当∠AOC=3∠BON时,求∠AOM的度数.
9.如图,已知∠AOB是直角,射线OC在∠AOB的外面,OM,ON分别是∠AOC和∠BOC的平分线.
(1)若∠BOC=40°求∠MON的大小;
(2)当∠BOC=60°,其它条件不变时,直接写出∠MON的度数;
(3)写出∠MON与∠AOB之间的数量关系(∠BOC<90°).
10.如图,点C表示村庄,AC,BC是两条公路,AB是河流.点A和点B处各有一座小桥.已知:AC⊥BC,CD⊥AB.
(1)量出点C到河边的图上距离是 cm;
(2)如果此图按照1:10000的比例画出的,计算出C到河边的实地距离为多少m;
(3)如果测量队测出∠ABC=28°,求出∠FAE的度数.
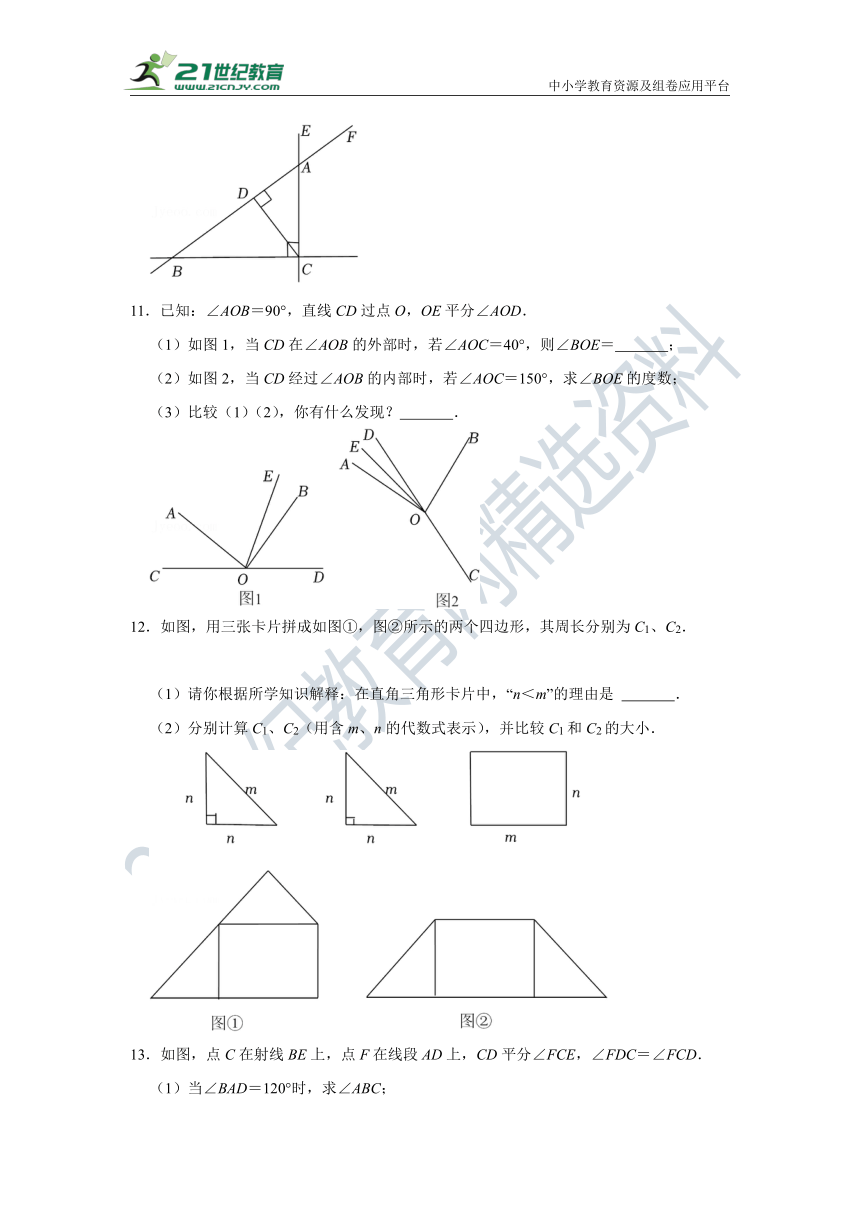
11.已知:∠AOB=90°,直线CD过点O,OE平分∠AOD.
(1)如图1,当CD在∠AOB的外部时,若∠AOC=40°,则∠BOE= ;
(2)如图2,当CD经过∠AOB的内部时,若∠AOC=150°,求∠BOE的度数;
(3)比较(1)(2),你有什么发现? .
12.如图,用三张卡片拼成如图①,图②所示的两个四边形,其周长分别为C1、C2.
(1)请你根据所学知识解释:在直角三角形卡片中,“n<m”的理由是 .
(2)分别计算C1、C2(用含m、n的代数式表示),并比较C1和C2的大小.
13.如图,点C在射线BE上,点F在线段AD上,CD平分∠FCE,∠FDC=∠FCD.
(1)当∠BAD=120°时,求∠ABC;
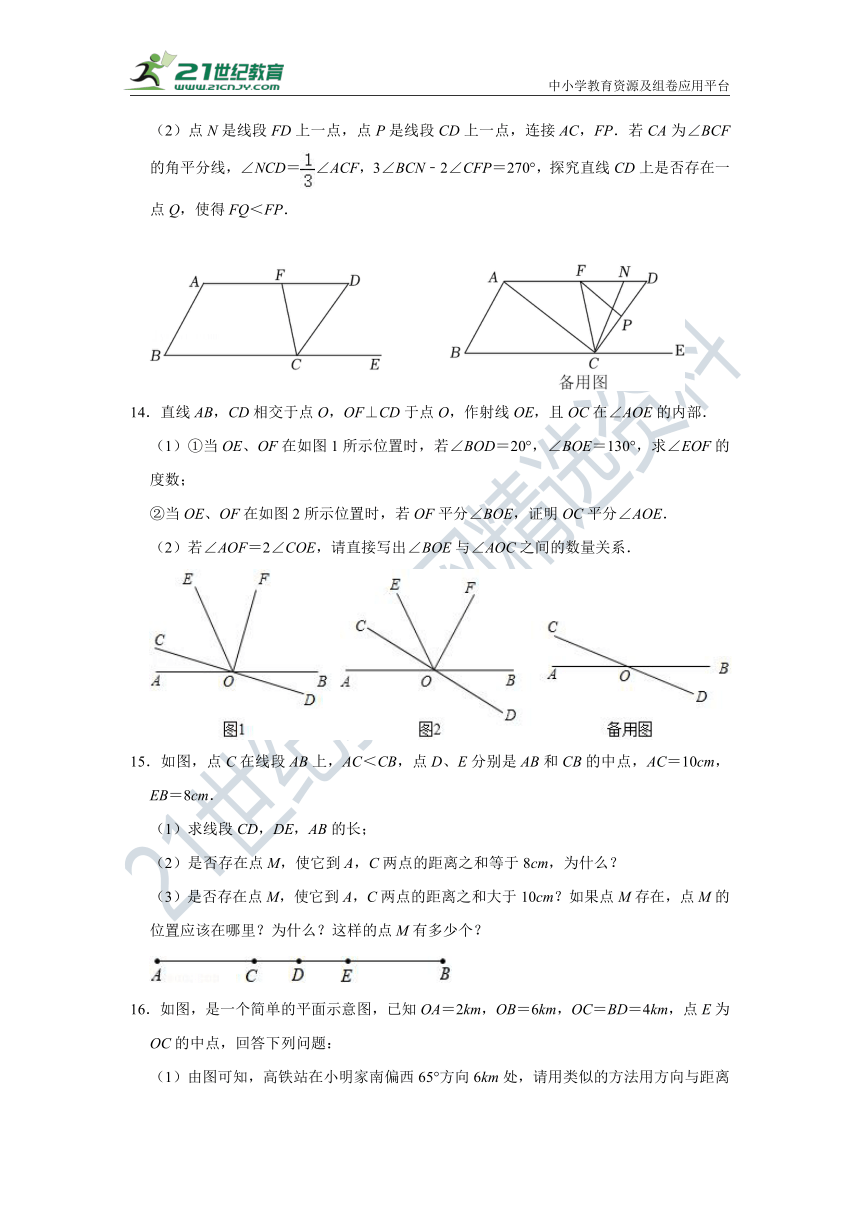
(2)点N是线段FD上一点,点P是线段CD上一点,连接AC,FP.若CA为∠BCF的角平分线,∠NCD=∠ACF,3∠BCN﹣2∠CFP=270°,探究直线CD上是否存在一点Q,使得FQ<FP.
14.直线AB,CD相交于点O,OF⊥CD于点O,作射线OE,且OC在∠AOE的内部.
(1)①当OE、OF在如图1所示位置时,若∠BOD=20°,∠BOE=130°,求∠EOF的度数;
②当OE、OF在如图2所示位置时,若OF平分∠BOE,证明OC平分∠AOE.
(2)若∠AOF=2∠COE,请直接写出∠BOE与∠AOC之间的数量关系.
15.如图,点C在线段AB上,AC<CB,点D、E分别是AB和CB的中点,AC=10cm,EB=8cm.
(1)求线段CD,DE,AB的长;
(2)是否存在点M,使它到A,C两点的距离之和等于8cm,为什么?
(3)是否存在点M,使它到A,C两点的距离之和大于10cm?如果点M存在,点M的位置应该在哪里?为什么?这样的点M有多少个?
16.如图,是一个简单的平面示意图,已知OA=2km,OB=6km,OC=BD=4km,点E为OC的中点,回答下列问题:
(1)由图可知,高铁站在小明家南偏西65°方向6km处,请用类似的方法用方向与距离描述学校、博物馆相对于小明家的位置;
(2)图中到小明家距离相同的是哪些地方?
17.如图,已知点C在线段AB上,且AM=AC,BN=BC.
(1)若AC=12,CB=6,求线段MN的长.
(2)若C为线段AB上任意一点,且满足AC+BC=a,其他条件不变,求线段MN的长.
18.已知射线OC在∠AOB的内部,若∠AOB,∠AOC和∠BOC三个角中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的奇妙线.
(1)一个角的平分线 这个角的奇妙线;(填“是”或“不是”)
(2)如图,∠MPN=60°.
①若射线PQ是∠MPN的奇妙线,则∠QPN的度数为 度;
②射线PF从PN位置开始,以每秒旋转3°45'的速度绕点P按逆时针方向旋转,当
∠FPN首次等于180°时停止旋转,设旋转的时间为t(s).当t为何值时,射线PM是∠FPN的奇妙线?
19.在平面直角坐标系中,D(0,﹣3),M(4,﹣3),直角三角形ABC的边与x轴分别相交于O、G两点,与直线DM分别交于E、F点,∠ACB=90°.
(1)将直角三角形如图1位置摆放,如果∠AOG=46°,则∠CEF= ;
(2)将直角三角形ABC如图2位置摆放,N为AC上一点,
①若∠NEC+∠CEF=180°,请直接写出∠NEF与∠AOG之间的等量关系: ;
②若∠NED+∠CEF=180°,请判断∠NEF与∠AOG之间的等量关系,并说明理由.
(3)将直角三角形ABC如图3位置摆放,若∠GOC=140°,延长AC交DM于点Q,点P是射线GF上一动点,探究∠POQ,∠OPQ与∠PQF的数量关系,请直接写出结论(题中的所有角都大于0°小于180°): .
20.以直线AB上一点O为端点作射线OC,使∠BOC=30°,将一个直角三角板的直角顶点放在O处,即∠DOE=90°.
(1)如图1,若直角三角板DOE的一边OE放在射线OA上,则∠COD= ;
(2)如图2,将直角三角板DOE绕点O顺时针转动到某个位置,
①若OE恰好平分∠AOC,则∠COD= ;
②若OD在∠BOC内部,请直接写由∠BOD与∠COE的数量关系为 ;
(3)将直角三角板DOE绕点O顺时针转动(与OB重合时为停止)的过程中,恰好有∠COD=∠AOE,求此时∠BOD的度数.
21.如图,O是直线EF上一点,OD是直线EF上方过点O的一条射线,∠DOE=70°,若射线OA在∠DOF的内部,∠AOD的度数为x(x<36°).射线OB在直线EF上方,且∠BOE=5∠AOD.
(1)∠AOE= (x的代数式表示);
(2)当∠AOB=30°时,求x的值;
(3)若射线OC在∠AOE的内部,且∠COE=4∠AOD,当OA,OB,OC三条射线中的一条射线是另外两条射线组成的夹角的平分线时,请直接写出x的值.
22.如图,将正方形纸片ABCD折叠,使点D落在BC边点E处,点A落在点F处,折痕为MN,若∠NEC=32°,求∠FMN的大小.
23.已知点O是直线AB上一点,过O作射线OC,使∠BOC=110°.
(1)如图1,∠AOC的度数是 ;
(2)如图2,过点O作射线OD使∠COD=90°,作∠AOC的平分线OE,求∠DOE的度数.
(3)在(2)的条件下,作射线OF,若∠BOF与∠AOE互余,请直接写出∠DOF的度数.
24.如图,直线AB,CD相交于点O,OB平分∠DOE,
(1)如图1,若∠COE=110°,求∠BOD的度数
(2)如图2,若∠BOE:∠COE=1:3,求∠AOC的度数;
(3)在(2)的条件下,画OF⊥CD,请直接写出∠EOF的度数.
参考答案
1.已知,∠AOD=160°,OB,OM,ON是∠AOD内的射线.
(1)如图1,若OM平分∠AOB,ON平分∠BOD,∠AOB=40°,则∠BON= 60 °;
(2)如图2,若OM平分∠AOB,ON平分∠BOD,求∠MON的度数;
(3)如图3,OC是∠AOD内的射线,若∠BOC=20°,OM平分∠AOC,ON平分∠BOD,当射线OB在∠AOC内时,求∠MON的度数.
【解答】解:(1)∵∠AOD=160°,∠AOB=40°,
∴∠BOD=120°,
∵ON平分∠BOD,
∴∠BON=∠BOD=60°,
故答案为:60;
(2)∵ON平分∠BOD,OM平分∠AOB,
∴∠BON=∠BOD,∠BOM=∠AOB,
∵∠AOD=160°,
∴∠MON=∠BON+∠BOM=∠BOD+∠AOB=∠AOD=80°;
(3)设∠AOB=x,则∠BOD=160°﹣x,
∵OM平分∠AOC,ON平分∠BOD,
∴∠COM=∠AOC=(x+20°),∠BON=∠BOD=(160°﹣x),
∴∠MON=∠COM+∠BON﹣∠BOC=(x+20°)+(160°﹣x)﹣20°=70°.
2.解答下列各题:
(1)图①,是一副三角尺(COD和AOB)在桌面上叠放成的图形,已知OB平分∠COD,则∠AOC度数是 67.5° ;
(2)如图②,点O在直线AB上.
①若∠1=40°,∠4=20°,则∠COE的度数是 120° .
②如果OD为任意射线,OC平分∠AOD,OE平分∠BOD,求∠COE的度数.
【解答】解:(1)由图得∠COD=45°,∠AOB=90°,
因为OB平分∠COD,
所以,
故答案为:22.5°;
所以∠AOC=∠AOB﹣∠COB=90°﹣22.5°=67.5°;
(2)①∵∠1=40°,∠4=20°,
∴∠COE=180°﹣∠1﹣∠4=120°,
故答案为:120°;
②因为点O在直线AB上,OD为任意射线,
所以∠AOD+∠BOD=180°,
因为OC平分∠AOD,OE平分∠BOD,
所以,(角平分线定义),
所以===90°.
3.已知:如图,O是直线AB上的一点,∠COD=90°,OE平分∠BOC.
(1)若∠AOC=30°,求∠COE的度数;
(2)若∠AOC=α,求∠DOE的度数(用含α的代数式表示).
【解答】解:(1)∵OE平分∠BOC,∠AOC=30°,
∴∠COB=180°﹣∠AOC=180°﹣30°=150°,
∴∠COE=150°×=75°.
(2))∵OE平分∠BOC,若∠AOC=α,
∴∠COB=180°﹣∠AOC=180°﹣α,
∴∠COE=(180°﹣α)×=90°﹣α,
∵∠COD=90°,
∴∠DOE=∠COD﹣∠COE=90°﹣(90°﹣α)=α.
4.如图1,已知∠AOB=60°,OM平分∠AOB.
(1)∠BOM= 30° ;
(2)若在图1中画射线OC,使得∠BOC=20°,ON平分∠BOC,求∠MON的大小;
(3)如图2,若线段OA与OB分别为同一钟表上某一时刻的时针与分针,∠AOB=60°,在时针与分针转动过程中,OM始终平分∠AOB,则经过多少分钟后,∠BOM的度数第一次等于50°.
【解答】解:(1)∵∠AOB=60°,OM平分∠AOB,
∴∠BOM=∠AOB=30°,
故答案为:30°;
(2)当OC在∠BOM内时,
∵∠BOC=20°,ON平分∠BOC,
∴∠BON=∠CON=10°,
∴∠MON=∠BOM﹣∠BON=30°﹣10°=20°;
当OC在∠BOM外时,
∵∠BOC=20°,ON平分∠BOC,
∴∠BON=∠CON=10°,
∴∠MON=∠BOM+∠BON=30°+10°=40°;
综上所述:∠MON为20°或40°;
(3)设经过t分钟,∠BOM的度数第一次等于50°,
∵∠BOM=50°,OM平分∠AOB,
∴∠AOB=100°,
∴60+6t﹣0.5t=100,
解得t=,
∴经过分钟,∠BOM的度数第一次等于50°.
5.如图所示,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)如果∠AOB=50°,∠DOE=35°,那么∠BOD是多少度?
(2)如果∠AOE=160°,∠COD=25°,那么∠AOB是多少度?
【解答】解:(1)∵OB是∠AOC的平分线,OD是∠COE的平分线,∠AOB=50°,∠DOE=35°,
∴∠BOC=∠AOB=50°,∠COD=∠DOE=35°,
∴∠BOD=∠BOC+∠COD=50°+35°=85°;
(2)∵OD是∠COE的平分线,∠COD=25°,
∴∠COE=2∠COD=2×25°=50°,
∵∠AOE=160°,
∴∠AOC=∠AOE﹣∠COE=160°﹣50°=110°,
∵OB是∠AOC的平分线,
∴∠AOB=∠AOC=×110°=55°.
6.已知∠AOB=∠COD=90°,OE平分∠AOC,OF平分∠BOD.
(1)如图1,若OB,OC重合,则∠EOF= 90° ;
(2)如图2,∠BOC=20°,求∠EOF的度数;
(3)如图3,求∠EOF的度数.
【解答】解:(1)∵OB,OC重合,
∴∠AOB+∠COD=180°.
∵OE平分∠AOC,OF平分∠BOD,
∴∠EOB=∠AOB,∠BOF=∠COD.
∴∠EOF=∠EOB+∠BOF
=∠AOB+∠COD
=(∠AOB+∠COD)
=×180°
=90°.
故答案为:90°.
(2)∵∠AOB=∠COD=90°,∠BOC=20°,
∴∠AOC=∠AOB ∠BOC=70°,∠BOD=∠COD ∠BOC=70°.
∵OE平分∠AOC,OF平分∠BOD,
∴∠EOC=∠AOC=35°,∠BOF=∠BOD=35°.
∴∠EOF=∠EOC+∠BOC+∠BOF=35°+20°+35°=90°.
(3)设∠BOC=x°.
∵∠AOB=∠COD=90°,∠BOC=x°,
∴∠AOC=∠AOB+∠BOC=(90+x)°,∠BOD=∠COD+∠BOC=(90+x)°.
∵OE平分∠AOC,OF平分∠BOD,
∴∠EOC=∠AOC=(90+x)°,∠BOF=∠BOD=(90+x)°.
∴∠EOF=∠EOC+∠BOF ∠BOC=(90+x)°+(90+x)° x°=90°.
7.如图,写出:
(1)以C为顶点的所有角;
(2)以AB为一边的所有角;
(3)以F为顶点,FB为一边的所有角.
【解答】解:(1)以C为顶点的所有角有∠BCE,∠BCF,∠BCD,∠ECF,∠ECD,∠FCD;
(2)以AB为一边的所有角有∠ABC,∠BAD,∠ABF;
(3)以F为顶点,FB为一边的所有角有∠AFB,∠BFC,∠BFD.
8.点O为直线AB上一点,将一直角三角板OMN的直角顶点放在点O处,射线OC平分∠MOB.
(1)如图1,若∠AOM=30°,求∠CON的度数;
(2)在图1中,若∠AOM=α,直接写出∠CON的度数(用含α的式子表示);
(3)将图1中的直角三角板OMN绕顶点O顺时针旋转至图2的位置,一边OM在直线AB上方,另一边ON在直线AB下方.
①探究∠AOM和∠CON的度数之间的关系,写出你的结论,并说明理由;
②当∠AOC=3∠BON时,求∠AOM的度数.
【解答】解:(1)由已知得∠BOM=180°﹣∠AOM=150°,
∵∠MON=90°,OC平分∠BOM,
∴∠CON=∠MON﹣∠BOM=90°﹣×150°=15°;
(2)由已知得∠BOM=180°﹣∠AOM=180°﹣a,
∵∠MON=90°,OC平分∠BOM,
∴∠CON=∠MON﹣∠BOM=90°﹣×(180°﹣a)=a;
(3)①设∠AOM=x,则∠BOM=180°﹣x,OC平分∠BOM,
∴∠MOC=∠BOM=(180°﹣x)=90°﹣,
∵∠MON=90°,
∴∠CON=∠MON﹣∠MOC=90°﹣(90°﹣x)=x,
∴∠CON=∠AOM;
②∵∠BON=∠MON﹣∠BOM=90°﹣(180°﹣x)=x﹣90°,
∴∠AOC=∠AOM+∠MOC=x+90°﹣=90°+x,
∵∠AOC=3∠BON,
∴90°+=3(x﹣90°),
解得x=144°,
∴∠AOM=144°.
9.如图,已知∠AOB是直角,射线OC在∠AOB的外面,OM,ON分别是∠AOC和∠BOC的平分线.
(1)若∠BOC=40°求∠MON的大小;
(2)当∠BOC=60°,其它条件不变时,直接写出∠MON的度数;
(3)写出∠MON与∠AOB之间的数量关系(∠BOC<90°).
【解答】解:(1)∵∠BOC=40°,ON是∠BOC的平分线,
∴∠NOC=∠BON=20°,
∵∠AOB是直角,
∴∠AOB=90°,
∴∠AOC=90°+40°=130°,
∵OM是∠AOC的平分线,
∴∠MOC=∠AOM=65°,
∴∠MON=∠MOC﹣∠NOC=65°﹣20°=45°;
(2)∵∠BOC=60°,ON是∠BOC的平分线,
∴∠NOC=∠BON=30°,
∵∠AOB是直角,
∴∠AOB=90°,
∴∠AOC=90°+60°=150°,
∵OM是∠AOC的平分线,
∴∠MOC=∠AOM=75°,
∴∠MON=∠MOC﹣∠NOC=75°﹣30°=45°;
(3)∠MON=∠AOB,
∵ON是∠BOC的平分线,
∴∠NOC=∠BOC,
∵∠AOB是直角,
∴∠AOB=90°,
∴∠AOC=90°+∠BOC,
∵OM是∠AOC的平分线,
∴∠MOC=∠AOC,
∴∠MON=∠MOC﹣∠NOC=∠AOC﹣∠BOC=(90°+∠BOC)﹣∠BOC=45°=∠AOB,
即∠MON=∠AOB.
10.如图,点C表示村庄,AC,BC是两条公路,AB是河流.点A和点B处各有一座小桥.已知:AC⊥BC,CD⊥AB.
(1)量出点C到河边的图上距离是 1.5 cm;
(2)如果此图按照1:10000的比例画出的,计算出C到河边的实地距离为多少m;
(3)如果测量队测出∠ABC=28°,求出∠FAE的度数.
【解答】解:(1)点C到AB的图上距离即线段CD的长度,测量可得点C到AB的图上距离是1.5厘米,
故答案为:1.5;
(2)1.5×10000=15000(厘米),
15000厘米=150米,
答:C到河边的实地距离为150米;
(3)∵AC⊥BC,∠ABC=28°,
∴∠BAC=90°﹣28°=62°,
∴∠EAF=∠BAC=62°.
11.已知:∠AOB=90°,直线CD过点O,OE平分∠AOD.
(1)如图1,当CD在∠AOB的外部时,若∠AOC=40°,则∠BOE= 20° ;
(2)如图2,当CD经过∠AOB的内部时,若∠AOC=150°,求∠BOE的度数;
(3)比较(1)(2),你有什么发现? ∠BOE=∠AOC. .
【解答】解:(1)∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∵∠AOC=40°,
∴∠DOB=50°,∠AOD=140°,
∵OE平分∠AOD,
∴∠DOE=∠AOD=70°,
∴∠BOE=∠DOE﹣∠DOB=70°﹣50°=20°.
故答案为:20°;
(2)∵∠AOC=150°,
∴∠AOD=30°,
∵OE平分∠AOD,
∴∠DOE=∠AOD=15°,
∵∠AOB=90°,
∴∠BOD=60°,
∴∠BOE=∠DOE+∠DOB=15°+60°=75°.
(3)∠BOE=∠AOC,
故答案为:∠BOE=∠AOC.
12.如图,用三张卡片拼成如图①,图②所示的两个四边形,其周长分别为C1、C2.
(1)请你根据所学知识解释:在直角三角形卡片中,“n<m”的理由是 垂线段最短 .
(2)分别计算C1、C2(用含m、n的代数式表示),并比较C1和C2的大小.
【解答】解:(1)在直角三角形卡片中,“n<m”的理由是垂线段最短,
故答案为:垂线段最短;
(2)如图所示,
C1=2m+4n;C2=4m+2n,
C1﹣C2=(2m+4n)﹣(4m+2n)=2n﹣2m=2(n﹣m),
∵n<m,
∴n﹣m<0,
∴2(n﹣m)<0,
∴C1<C2.
13.如图,点C在射线BE上,点F在线段AD上,CD平分∠FCE,∠FDC=∠FCD.
(1)当∠BAD=120°时,求∠ABC;
(2)点N是线段FD上一点,点P是线段CD上一点,连接AC,FP.若CA为∠BCF的角平分线,∠NCD=∠ACF,3∠BCN﹣2∠CFP=270°,探究直线CD上是否存在一点Q,使得FQ<FP.
【解答】解:(1)∵CD平分∠FCE,
∴∠DCF=∠DCE,
∵∠FDC=∠FCD,
∴∠FDC=∠DCE,
∴AD∥BE,
∴∠A+∠B=180°,
∵∠A=120°,
∴∠B=60°;
(2)∵CA为∠BCF的角平分线,
∴∠BCA=∠ACF,
∵∠BCA+∠ACF+∠DCF+∠DCE=180°,
∵∠DCF=∠DCE,
∴∠ACF+∠DCF=90°,
∴AC⊥CD,
设∠NCD=x,∠FCN=y,
∵∠NCD=∠ACF,
∴∠ACF=∠BCA=3x,
∵3∠BCN﹣2∠CFP=270°,
∴18x+3y+2∠CFP=270°①,
∵4x+y=90°②,
∴由①②消去y得∠CFP=3x,
∴∠CFP=∠ACF,
∴FP∥AC,
∴FP⊥CD,
∵垂线段最短,
∴直线CD上不存在一点Q,使得FQ<FP.
14.直线AB,CD相交于点O,OF⊥CD于点O,作射线OE,且OC在∠AOE的内部.
(1)①当OE、OF在如图1所示位置时,若∠BOD=20°,∠BOE=130°,求∠EOF的度数;
②当OE、OF在如图2所示位置时,若OF平分∠BOE,证明OC平分∠AOE.
(2)若∠AOF=2∠COE,请直接写出∠BOE与∠AOC之间的数量关系.
【解答】(1)①解:∵OF⊥CD于点O,
∴∠DOF=90°,
∵∠BOD=20°,
∴∠BOF=90°﹣20°=70°,
∵∠BOE=130°,
∴∠EOF=∠BOE﹣∠BOF=130°﹣70°=60°;
∴∠EOF的度数为60°;
②证明:∵OF平分∠BOE,
∴∠EOF=∠FOB=∠EOB,
∵OF⊥CD,
∴∠COF=90°,
∴∠COE+∠EOF=∠AOC+∠BOF=90°,
∴∠COE=∠AOC,即OC平分∠AOE;
(2)解:3∠AOC+2∠BOE=270°或∠AOC+2∠BOE=270°,
理由如下:
当点E,F在直线AB的同侧时,如图,
记∠COE=α,则∠AOF=2∠COE=2α,
∵OF⊥CD,
∴∠COF=90°,
∴∠EOF=90°﹣α,∠AOC=∠AOF﹣∠COF=2α﹣90°①,
∴∠BOE=180°﹣∠AOC﹣∠COE=180°﹣(2α﹣90°)﹣α=270°﹣3α②,
①×3+②×2得,3∠AOC+2∠BOE=270°;
当点E和点F在直线AB的异侧时,如图,
记∠COE=α,则∠AOF=2∠COE=2α,
∵OF⊥CD,
∴∠COF=90°,
∴∠AOC=∠COF﹣∠AOF=90°﹣2α①,
∴∠BOE=180°﹣∠AOC﹣∠COE=180°﹣(90°﹣2α)﹣α=90°+α②,
①+2×②得,∠AOC+2∠BOE=270°.
综上可知,3∠AOC+2∠BOE=270°或∠AOC+2∠BOE=270°.
15.如图,点C在线段AB上,AC<CB,点D、E分别是AB和CB的中点,AC=10cm,EB=8cm.
(1)求线段CD,DE,AB的长;
(2)是否存在点M,使它到A,C两点的距离之和等于8cm,为什么?
(3)是否存在点M,使它到A,C两点的距离之和大于10cm?如果点M存在,点M的位置应该在哪里?为什么?这样的点M有多少个?
【解答】解:(1)∵点E是CB的中点,EB=8cm,
∴CE=BE=8cm,
∴BC=CE+BE=8+8=16(cm),
∵AC=10cm,
∴AB=26cm,
∵点D是AB的中点,
∴AD=BD=13cm,
∴CD=AD﹣AC=13﹣10=3(cm),
DE=BD﹣BE=13﹣8=5(cm);
(2)不存在,
∵两点之间线段最短,
∴点A、C之间的最短距离为10cm,
故不存在点M,使它到A,C两点的距离之和等于8cm;
(3)存在,
∵两点之间线段最短,
∴线段AB外任何一点到A,C两点的距离之和都大于10cm,这样的点有无数个.
16.如图,是一个简单的平面示意图,已知OA=2km,OB=6km,OC=BD=4km,点E为OC的中点,回答下列问题:
(1)由图可知,高铁站在小明家南偏西65°方向6km处,请用类似的方法用方向与距离描述学校、博物馆相对于小明家的位置;
(2)图中到小明家距离相同的是哪些地方?
【解答】解:(1)由题意得:
90°﹣45°=45°,90°﹣40°=50°,
学校在小明家北偏东45°方向2km处,
博物馆在小明家南偏东50°方向4km处;
(2)∵OC=4km,点E为OC的中点,
∴OE=OC=2(km),
∵OB=6km,BD=4km,
∴OD=OB﹣BD=2(km),
∵OA=2km,
∴OA=OD=OE,
∴图中到小明家距离相同的是影院,公园,学校.
17.如图,已知点C在线段AB上,且AM=AC,BN=BC.
(1)若AC=12,CB=6,求线段MN的长.
(2)若C为线段AB上任意一点,且满足AC+BC=a,其他条件不变,求线段MN的长.
【解答】解:(1)∵AM=AC,
∴CM=AC,
∵AC=12,
∴CM=8,
∵BN=BC,
∴CN=BC,
∵BC=6,
∴CN=×6=4,
∴MN=CM+CN=8+4=12;
(2)∵AM=AC,BN=BC,
∴AM+BN=AC+BC=(AC+BC),
∴MN=MC+NC=(AC+BC),
∵AC+BC=a,
∴MN=a,
即线段MN的长为a.
18.已知射线OC在∠AOB的内部,若∠AOB,∠AOC和∠BOC三个角中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的奇妙线.
(1)一个角的平分线 是 这个角的奇妙线;(填“是”或“不是”)
(2)如图,∠MPN=60°.
①若射线PQ是∠MPN的奇妙线,则∠QPN的度数为 20或30或40 度;
②射线PF从PN位置开始,以每秒旋转3°45'的速度绕点P按逆时针方向旋转,当
∠FPN首次等于180°时停止旋转,设旋转的时间为t(s).当t为何值时,射线PM是∠FPN的奇妙线?
【解答】解:(1)一个角的平分线是这个角的“奇妙线”;
故答案为:是.
(2)①若∠MPN=60°,且射线PQ是∠MPN的“奇妙线”,则由“奇妙线”的定义可知有三种情况符合题意:
当∠NPQ=2∠MPQ时,∠QPN=40°,
当∠MPQ=2∠NPQ时,∠QPN=20°,
当∠NPM=2∠MPQ时,∠QPN=30°,
故答案为:20或30或40;
②依题意有,3°45′=3.75°,
当3.75t=60+×60时,
解得t=24;
当3.75t=2×60时,
解得t=32;
当3.75t=60+2×60时,
解得t=48.
故当t为24或32或48时,射线PM是∠FPN的“奇妙线”;
19.在平面直角坐标系中,D(0,﹣3),M(4,﹣3),直角三角形ABC的边与x轴分别相交于O、G两点,与直线DM分别交于E、F点,∠ACB=90°.
(1)将直角三角形如图1位置摆放,如果∠AOG=46°,则∠CEF= 136° ;
(2)将直角三角形ABC如图2位置摆放,N为AC上一点,
①若∠NEC+∠CEF=180°,请直接写出∠NEF与∠AOG之间的等量关系: ∠NEF=2∠AOG ;
②若∠NED+∠CEF=180°,请判断∠NEF与∠AOG之间的等量关系,并说明理由.
(3)将直角三角形ABC如图3位置摆放,若∠GOC=140°,延长AC交DM于点Q,点P是射线GF上一动点,探究∠POQ,∠OPQ与∠PQF的数量关系,请直接写出结论(题中的所有角都大于0°小于180°): OPQ=140°﹣∠POQ+∠PQF或140°﹣∠POQ=∠OPQ+∠PQF .
【解答】解:(1)过点C作CP∥DM,
∵D(0,﹣3),M(4,﹣3),
∴DM∥x轴,
∴CP∥DM∥x轴,
∴∠AOG=∠ACP,∠BCP+∠CEF=180°,
∴∠BCP=180°﹣∠CEF,
∵∠ACP+∠BCP=90°,
∴∠AOG+180°﹣∠CEF=90°,
∵∠AOG=46°,
∴∠CEF=136°.
故答案为:136°.
(2)①过点C作CQ∥x轴,
∴CQ∥EM∥x轴,
∴∠AOG=∠ACQ,∠ECQ=∠CEK,
∵∠NEC+∠CEF=180°,∠CEK+∠CEF=180°,
∴∠NEC=∠CEK,
∵∠ACQ+∠ECQ=90°,
∴∠ECQ=∠CEK=∠NEC=90°﹣∠ACQ=90°﹣∠AOG,
∵∠CEK+∠NEC+∠NEF=180°,
∴2(90°﹣∠AOG)+∠NEF=180°,
整理得∠NEF=2∠AOG.
故答案为:∠NEF=2∠AOG.
②∠NEF+∠AOG=90°.
理由如下:
∵CQ∥EM∥x轴,
∴∠AOG=∠ACQ,∠ECQ=∠CEK,
∵∠NED+∠CEF=180°,∠CEK+∠CEF=180°,
∴∠NED=∠CEK,
∵∠ACQ+∠ECQ=90°,
∴∠AOG+∠NEF=90°.
(3)当点P在GF上时,过点P作PH∥OG,
∴PH∥OG∥DM,
∴∠GOP=∠OPH,∠PQF=∠HPQ,
∴∠OPQ=∠GOP+∠PQF,
∴∠OPQ=140°﹣∠POQ+∠PQF.
当点P在线段GF的延长线上时,
∴PR∥OG∥DM,
∴∠GOP=∠OPR,∠PQF=∠QPR,
∵∠OPR=∠OPQ+∠QPR,
∴∠GOP=∠OPQ+∠PQF,
∴140°﹣∠POQ=∠OPQ+∠PQF.
故答案为:∠OPQ=140°﹣∠POQ+∠PQF或140°﹣∠POQ=∠OPQ+∠PQF.
20.以直线AB上一点O为端点作射线OC,使∠BOC=30°,将一个直角三角板的直角顶点放在O处,即∠DOE=90°.
(1)如图1,若直角三角板DOE的一边OE放在射线OA上,则∠COD= 60° ;
(2)如图2,将直角三角板DOE绕点O顺时针转动到某个位置,
①若OE恰好平分∠AOC,则∠COD= 15° ;
②若OD在∠BOC内部,请直接写由∠BOD与∠COE的数量关系为 ∠COE=∠BOD+30° ;
(3)将直角三角板DOE绕点O顺时针转动(与OB重合时为停止)的过程中,恰好有∠COD=∠AOE,求此时∠BOD的度数.
【解答】解:(1)∵∠BOD=90°,∠BOC=30°,
∴∠COD=∠BOD﹣∠BOC=90°﹣30°=60°.
故答案为:60°;
(2)①∵∠AOC=∠AOD+∠COD,
∴∠AOC=90°+60°=150°,
∵OE平分∠AOC,
∴,
∴∠COD=90°﹣∠COE=90°﹣75°=15°;
故答案为:15°;
②∵∠COE+∠COD=90°,
∠BOD+∠COD=30°,
∴∠COD=∠BOD+30°;
故答案为:∠COD=∠BOD+30°;
(3)∵∠COD+∠COE=90°,∠COE+∠AOE=150°,
∴∠AOE=60°+∠COD,
∵∠COD=∠AOE,
∴∠COD=15°,
∴∠BOD=∠BOC﹣∠COD=30°﹣15°=15°.
21.如图,O是直线EF上一点,OD是直线EF上方过点O的一条射线,∠DOE=70°,若射线OA在∠DOF的内部,∠AOD的度数为x(x<36°).射线OB在直线EF上方,且∠BOE=5∠AOD.
(1)∠AOE= x+70° (x的代数式表示);
(2)当∠AOB=30°时,求x的值;
(3)若射线OC在∠AOE的内部,且∠COE=4∠AOD,当OA,OB,OC三条射线中的一条射线是另外两条射线组成的夹角的平分线时,请直接写出x的值.
【解答】解:(1)∠AOE=x+70°.
故答案为:x+70°;
(2)①当射线OB在OA左边时,
∵∠BOE=5∠AOD,∠AOB=30°,∠AOD的度数为x(x<36°).
∴∠AOB=∠AOE﹣∠BOE,
∴70°+x﹣5x=30°,解得x=10°;
②当射线OB在OA右边时,
∵∠BOE=5∠AOD,∠AOB=30°,∠AOD的度数为x(x<36°).
∴∠AOB=∠BOE﹣∠AOE,
∴5x﹣70°﹣x=30°,解得x=25°;
综上,x的值为10或25;
(3)x的值为14,20,35.
∵∠COE=4∠AOD=4x,∠BOE=5∠AOD=5x.
∴∠COE<∠BOE,
∴射线OC在OB的左边,
①当OB为∠AOC的平分线时,
∵∠AOB=∠AOE﹣∠BOE=70°+x﹣5x=70°﹣4x,
∠BOC=∠BOE﹣∠COE=5x﹣4x=x,
∴70°﹣4x=x,
解得:x=14°;
②当OA为∠BOC的平分线时,
∵∠AOB=∠BOE﹣∠AOE=5x﹣70°﹣x=4x﹣70°,
∠AOC=∠AOE﹣∠COE=70°+x﹣4x=70°﹣3x,
∴4x﹣70°=70°﹣3x,
解得:x=20°;
综上,满足条件的x的值为14,20,35.
22.如图,将正方形纸片ABCD折叠,使点D落在BC边点E处,点A落在点F处,折痕为MN,若∠NEC=32°,求∠FMN的大小.
【解答】解:∵四边形ABCD是正方形,正方形纸片ABCD折叠,使点D落在BC边点E处,点A落在点F处,
∴∠F=∠A=90°,∠DNM=∠ENM,∠FEN=∠D=90°,
∵∠NEC=32°,
∴∠ENC=90°﹣32°=58°,
∴,
∴∠FMN=360°﹣90°﹣90°﹣61°=119°.
23.已知点O是直线AB上一点,过O作射线OC,使∠BOC=110°.
(1)如图1,∠AOC的度数是 70° ;
(2)如图2,过点O作射线OD使∠COD=90°,作∠AOC的平分线OE,求∠DOE的度数.
(3)在(2)的条件下,作射线OF,若∠BOF与∠AOE互余,请直接写出∠DOF的度数.
【解答】解:(1)∵∠AOC+∠BOC=180°,∠BOC=110°,
∴∠AOC=180°﹣110°=70°,
故答案为:70°;
(2)∵OE是∠AOC的平分线,
∴∠AOE=∠COE=∠AOC=35°,
又∵∠COD=90°,
∴∠DOE=∠COE+∠COD=125°;
(3)由(2)得∠AOE=35°,∠BOD=110°﹣90°=20°,
∵∠BOF与∠AOE互余,
∴∠BOF=90°﹣35°=55°,
①当射线OF在射线OB的上方时,有∠DOF=∠BOF﹣∠BOD=55°﹣20°=35°,
②当射线OF在射线OB的下方时,有∠DOF=∠BOF+∠BOD=55°+20°=75°,
答:∠DOF的度数为35°或75°.
24.如图,直线AB,CD相交于点O,OB平分∠DOE,
(1)如图1,若∠COE=110°,求∠BOD的度数
(2)如图2,若∠BOE:∠COE=1:3,求∠AOC的度数;
(3)在(2)的条件下,画OF⊥CD,请直接写出∠EOF的度数.
【解答】解:(1)∵∠COE+∠DOE=180°,∠COE=110°,
∴∠DOE=180°﹣110°=70°,
又∵OB平分∠DOE,
∴∠BOD=∠BOE=∠DOE=35°;
(2)∵OB平分∠DOE,
∴∠BOD=∠BOE=∠DOE,
∵∠BOE:∠COE=1:3,
∴∠BOD=180°×=36°,
∴∠AOC=∠BOD=36°;
(3)由(2)得∠DOE=72°,
当OF在直线CD的上方时,有∠EOF=∠FOD+∠DOE=90°+72°=162°,
当OF在直线CD的下方时,有∠EOF=∠FOD﹣∠DOE=90°﹣72°=18°,
因此∠EOF的度数为18°或162°.
几何图形初步解答题专项练习
1.已知,∠AOD=160°,OB,OM,ON是∠AOD内的射线.
(1)如图1,若OM平分∠AOB,ON平分∠BOD,∠AOB=40°,则∠BON= °;
(2)如图2,若OM平分∠AOB,ON平分∠BOD,求∠MON的度数;
(3)如图3,OC是∠AOD内的射线,若∠BOC=20°,OM平分∠AOC,ON平分∠BOD,当射线OB在∠AOC内时,求∠MON的度数.
2.解答下列各题:
(1)图①,是一副三角尺(COD和AOB)在桌面上叠放成的图形,已知OB平分∠COD,则∠AOC度数是 ;
(2)如图②,点O在直线AB上.
①若∠1=40°,∠4=20°,则∠COE的度数是 .
②如果OD为任意射线,OC平分∠AOD,OE平分∠BOD,求∠COE的度数.
3.已知:如图,O是直线AB上的一点,∠COD=90°,OE平分∠BOC.
(1)若∠AOC=30°,求∠COE的度数;
(2)若∠AOC=α,求∠DOE的度数(用含α的代数式表示).
4.如图1,已知∠AOB=60°,OM平分∠AOB.
(1)∠BOM= ;
(2)若在图1中画射线OC,使得∠BOC=20°,ON平分∠BOC,求∠MON的大小;
(3)如图2,若线段OA与OB分别为同一钟表上某一时刻的时针与分针,∠AOB=60°,在时针与分针转动过程中,OM始终平分∠AOB,则经过多少分钟后,∠BOM的度数第一次等于50°.
5.如图所示,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)如果∠AOB=50°,∠DOE=35°,那么∠BOD是多少度?
(2)如果∠AOE=160°,∠COD=25°,那么∠AOB是多少度?
6.已知∠AOB=∠COD=90°,OE平分∠AOC,OF平分∠BOD.
(1)如图1,若OB,OC重合,则∠EOF= ;
(2)如图2,∠BOC=20°,求∠EOF的度数;
(3)如图3,求∠EOF的度数.
7.如图,写出:
(1)以C为顶点的所有角;
(2)以AB为一边的所有角;
(3)以F为顶点,FB为一边的所有角.
8.点O为直线AB上一点,将一直角三角板OMN的直角顶点放在点O处,射线OC平分∠MOB.
(1)如图1,若∠AOM=30°,求∠CON的度数;
(2)在图1中,若∠AOM=α,直接写出∠CON的度数(用含α的式子表示);
(3)将图1中的直角三角板OMN绕顶点O顺时针旋转至图2的位置,一边OM在直线AB上方,另一边ON在直线AB下方.
①探究∠AOM和∠CON的度数之间的关系,写出你的结论,并说明理由;
②当∠AOC=3∠BON时,求∠AOM的度数.
9.如图,已知∠AOB是直角,射线OC在∠AOB的外面,OM,ON分别是∠AOC和∠BOC的平分线.
(1)若∠BOC=40°求∠MON的大小;
(2)当∠BOC=60°,其它条件不变时,直接写出∠MON的度数;
(3)写出∠MON与∠AOB之间的数量关系(∠BOC<90°).
10.如图,点C表示村庄,AC,BC是两条公路,AB是河流.点A和点B处各有一座小桥.已知:AC⊥BC,CD⊥AB.
(1)量出点C到河边的图上距离是 cm;
(2)如果此图按照1:10000的比例画出的,计算出C到河边的实地距离为多少m;
(3)如果测量队测出∠ABC=28°,求出∠FAE的度数.
11.已知:∠AOB=90°,直线CD过点O,OE平分∠AOD.
(1)如图1,当CD在∠AOB的外部时,若∠AOC=40°,则∠BOE= ;
(2)如图2,当CD经过∠AOB的内部时,若∠AOC=150°,求∠BOE的度数;
(3)比较(1)(2),你有什么发现? .
12.如图,用三张卡片拼成如图①,图②所示的两个四边形,其周长分别为C1、C2.
(1)请你根据所学知识解释:在直角三角形卡片中,“n<m”的理由是 .
(2)分别计算C1、C2(用含m、n的代数式表示),并比较C1和C2的大小.
13.如图,点C在射线BE上,点F在线段AD上,CD平分∠FCE,∠FDC=∠FCD.
(1)当∠BAD=120°时,求∠ABC;
(2)点N是线段FD上一点,点P是线段CD上一点,连接AC,FP.若CA为∠BCF的角平分线,∠NCD=∠ACF,3∠BCN﹣2∠CFP=270°,探究直线CD上是否存在一点Q,使得FQ<FP.
14.直线AB,CD相交于点O,OF⊥CD于点O,作射线OE,且OC在∠AOE的内部.
(1)①当OE、OF在如图1所示位置时,若∠BOD=20°,∠BOE=130°,求∠EOF的度数;
②当OE、OF在如图2所示位置时,若OF平分∠BOE,证明OC平分∠AOE.
(2)若∠AOF=2∠COE,请直接写出∠BOE与∠AOC之间的数量关系.
15.如图,点C在线段AB上,AC<CB,点D、E分别是AB和CB的中点,AC=10cm,EB=8cm.
(1)求线段CD,DE,AB的长;
(2)是否存在点M,使它到A,C两点的距离之和等于8cm,为什么?
(3)是否存在点M,使它到A,C两点的距离之和大于10cm?如果点M存在,点M的位置应该在哪里?为什么?这样的点M有多少个?
16.如图,是一个简单的平面示意图,已知OA=2km,OB=6km,OC=BD=4km,点E为OC的中点,回答下列问题:
(1)由图可知,高铁站在小明家南偏西65°方向6km处,请用类似的方法用方向与距离描述学校、博物馆相对于小明家的位置;
(2)图中到小明家距离相同的是哪些地方?
17.如图,已知点C在线段AB上,且AM=AC,BN=BC.
(1)若AC=12,CB=6,求线段MN的长.
(2)若C为线段AB上任意一点,且满足AC+BC=a,其他条件不变,求线段MN的长.
18.已知射线OC在∠AOB的内部,若∠AOB,∠AOC和∠BOC三个角中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的奇妙线.
(1)一个角的平分线 这个角的奇妙线;(填“是”或“不是”)
(2)如图,∠MPN=60°.
①若射线PQ是∠MPN的奇妙线,则∠QPN的度数为 度;
②射线PF从PN位置开始,以每秒旋转3°45'的速度绕点P按逆时针方向旋转,当
∠FPN首次等于180°时停止旋转,设旋转的时间为t(s).当t为何值时,射线PM是∠FPN的奇妙线?
19.在平面直角坐标系中,D(0,﹣3),M(4,﹣3),直角三角形ABC的边与x轴分别相交于O、G两点,与直线DM分别交于E、F点,∠ACB=90°.
(1)将直角三角形如图1位置摆放,如果∠AOG=46°,则∠CEF= ;
(2)将直角三角形ABC如图2位置摆放,N为AC上一点,
①若∠NEC+∠CEF=180°,请直接写出∠NEF与∠AOG之间的等量关系: ;
②若∠NED+∠CEF=180°,请判断∠NEF与∠AOG之间的等量关系,并说明理由.
(3)将直角三角形ABC如图3位置摆放,若∠GOC=140°,延长AC交DM于点Q,点P是射线GF上一动点,探究∠POQ,∠OPQ与∠PQF的数量关系,请直接写出结论(题中的所有角都大于0°小于180°): .
20.以直线AB上一点O为端点作射线OC,使∠BOC=30°,将一个直角三角板的直角顶点放在O处,即∠DOE=90°.
(1)如图1,若直角三角板DOE的一边OE放在射线OA上,则∠COD= ;
(2)如图2,将直角三角板DOE绕点O顺时针转动到某个位置,
①若OE恰好平分∠AOC,则∠COD= ;
②若OD在∠BOC内部,请直接写由∠BOD与∠COE的数量关系为 ;
(3)将直角三角板DOE绕点O顺时针转动(与OB重合时为停止)的过程中,恰好有∠COD=∠AOE,求此时∠BOD的度数.
21.如图,O是直线EF上一点,OD是直线EF上方过点O的一条射线,∠DOE=70°,若射线OA在∠DOF的内部,∠AOD的度数为x(x<36°).射线OB在直线EF上方,且∠BOE=5∠AOD.
(1)∠AOE= (x的代数式表示);
(2)当∠AOB=30°时,求x的值;
(3)若射线OC在∠AOE的内部,且∠COE=4∠AOD,当OA,OB,OC三条射线中的一条射线是另外两条射线组成的夹角的平分线时,请直接写出x的值.
22.如图,将正方形纸片ABCD折叠,使点D落在BC边点E处,点A落在点F处,折痕为MN,若∠NEC=32°,求∠FMN的大小.
23.已知点O是直线AB上一点,过O作射线OC,使∠BOC=110°.
(1)如图1,∠AOC的度数是 ;
(2)如图2,过点O作射线OD使∠COD=90°,作∠AOC的平分线OE,求∠DOE的度数.
(3)在(2)的条件下,作射线OF,若∠BOF与∠AOE互余,请直接写出∠DOF的度数.
24.如图,直线AB,CD相交于点O,OB平分∠DOE,
(1)如图1,若∠COE=110°,求∠BOD的度数
(2)如图2,若∠BOE:∠COE=1:3,求∠AOC的度数;
(3)在(2)的条件下,画OF⊥CD,请直接写出∠EOF的度数.
参考答案
1.已知,∠AOD=160°,OB,OM,ON是∠AOD内的射线.
(1)如图1,若OM平分∠AOB,ON平分∠BOD,∠AOB=40°,则∠BON= 60 °;
(2)如图2,若OM平分∠AOB,ON平分∠BOD,求∠MON的度数;
(3)如图3,OC是∠AOD内的射线,若∠BOC=20°,OM平分∠AOC,ON平分∠BOD,当射线OB在∠AOC内时,求∠MON的度数.
【解答】解:(1)∵∠AOD=160°,∠AOB=40°,
∴∠BOD=120°,
∵ON平分∠BOD,
∴∠BON=∠BOD=60°,
故答案为:60;
(2)∵ON平分∠BOD,OM平分∠AOB,
∴∠BON=∠BOD,∠BOM=∠AOB,
∵∠AOD=160°,
∴∠MON=∠BON+∠BOM=∠BOD+∠AOB=∠AOD=80°;
(3)设∠AOB=x,则∠BOD=160°﹣x,
∵OM平分∠AOC,ON平分∠BOD,
∴∠COM=∠AOC=(x+20°),∠BON=∠BOD=(160°﹣x),
∴∠MON=∠COM+∠BON﹣∠BOC=(x+20°)+(160°﹣x)﹣20°=70°.
2.解答下列各题:
(1)图①,是一副三角尺(COD和AOB)在桌面上叠放成的图形,已知OB平分∠COD,则∠AOC度数是 67.5° ;
(2)如图②,点O在直线AB上.
①若∠1=40°,∠4=20°,则∠COE的度数是 120° .
②如果OD为任意射线,OC平分∠AOD,OE平分∠BOD,求∠COE的度数.
【解答】解:(1)由图得∠COD=45°,∠AOB=90°,
因为OB平分∠COD,
所以,
故答案为:22.5°;
所以∠AOC=∠AOB﹣∠COB=90°﹣22.5°=67.5°;
(2)①∵∠1=40°,∠4=20°,
∴∠COE=180°﹣∠1﹣∠4=120°,
故答案为:120°;
②因为点O在直线AB上,OD为任意射线,
所以∠AOD+∠BOD=180°,
因为OC平分∠AOD,OE平分∠BOD,
所以,(角平分线定义),
所以===90°.
3.已知:如图,O是直线AB上的一点,∠COD=90°,OE平分∠BOC.
(1)若∠AOC=30°,求∠COE的度数;
(2)若∠AOC=α,求∠DOE的度数(用含α的代数式表示).
【解答】解:(1)∵OE平分∠BOC,∠AOC=30°,
∴∠COB=180°﹣∠AOC=180°﹣30°=150°,
∴∠COE=150°×=75°.
(2))∵OE平分∠BOC,若∠AOC=α,
∴∠COB=180°﹣∠AOC=180°﹣α,
∴∠COE=(180°﹣α)×=90°﹣α,
∵∠COD=90°,
∴∠DOE=∠COD﹣∠COE=90°﹣(90°﹣α)=α.
4.如图1,已知∠AOB=60°,OM平分∠AOB.
(1)∠BOM= 30° ;
(2)若在图1中画射线OC,使得∠BOC=20°,ON平分∠BOC,求∠MON的大小;
(3)如图2,若线段OA与OB分别为同一钟表上某一时刻的时针与分针,∠AOB=60°,在时针与分针转动过程中,OM始终平分∠AOB,则经过多少分钟后,∠BOM的度数第一次等于50°.
【解答】解:(1)∵∠AOB=60°,OM平分∠AOB,
∴∠BOM=∠AOB=30°,
故答案为:30°;
(2)当OC在∠BOM内时,
∵∠BOC=20°,ON平分∠BOC,
∴∠BON=∠CON=10°,
∴∠MON=∠BOM﹣∠BON=30°﹣10°=20°;
当OC在∠BOM外时,
∵∠BOC=20°,ON平分∠BOC,
∴∠BON=∠CON=10°,
∴∠MON=∠BOM+∠BON=30°+10°=40°;
综上所述:∠MON为20°或40°;
(3)设经过t分钟,∠BOM的度数第一次等于50°,
∵∠BOM=50°,OM平分∠AOB,
∴∠AOB=100°,
∴60+6t﹣0.5t=100,
解得t=,
∴经过分钟,∠BOM的度数第一次等于50°.
5.如图所示,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)如果∠AOB=50°,∠DOE=35°,那么∠BOD是多少度?
(2)如果∠AOE=160°,∠COD=25°,那么∠AOB是多少度?
【解答】解:(1)∵OB是∠AOC的平分线,OD是∠COE的平分线,∠AOB=50°,∠DOE=35°,
∴∠BOC=∠AOB=50°,∠COD=∠DOE=35°,
∴∠BOD=∠BOC+∠COD=50°+35°=85°;
(2)∵OD是∠COE的平分线,∠COD=25°,
∴∠COE=2∠COD=2×25°=50°,
∵∠AOE=160°,
∴∠AOC=∠AOE﹣∠COE=160°﹣50°=110°,
∵OB是∠AOC的平分线,
∴∠AOB=∠AOC=×110°=55°.
6.已知∠AOB=∠COD=90°,OE平分∠AOC,OF平分∠BOD.
(1)如图1,若OB,OC重合,则∠EOF= 90° ;
(2)如图2,∠BOC=20°,求∠EOF的度数;
(3)如图3,求∠EOF的度数.
【解答】解:(1)∵OB,OC重合,
∴∠AOB+∠COD=180°.
∵OE平分∠AOC,OF平分∠BOD,
∴∠EOB=∠AOB,∠BOF=∠COD.
∴∠EOF=∠EOB+∠BOF
=∠AOB+∠COD
=(∠AOB+∠COD)
=×180°
=90°.
故答案为:90°.
(2)∵∠AOB=∠COD=90°,∠BOC=20°,
∴∠AOC=∠AOB ∠BOC=70°,∠BOD=∠COD ∠BOC=70°.
∵OE平分∠AOC,OF平分∠BOD,
∴∠EOC=∠AOC=35°,∠BOF=∠BOD=35°.
∴∠EOF=∠EOC+∠BOC+∠BOF=35°+20°+35°=90°.
(3)设∠BOC=x°.
∵∠AOB=∠COD=90°,∠BOC=x°,
∴∠AOC=∠AOB+∠BOC=(90+x)°,∠BOD=∠COD+∠BOC=(90+x)°.
∵OE平分∠AOC,OF平分∠BOD,
∴∠EOC=∠AOC=(90+x)°,∠BOF=∠BOD=(90+x)°.
∴∠EOF=∠EOC+∠BOF ∠BOC=(90+x)°+(90+x)° x°=90°.
7.如图,写出:
(1)以C为顶点的所有角;
(2)以AB为一边的所有角;
(3)以F为顶点,FB为一边的所有角.
【解答】解:(1)以C为顶点的所有角有∠BCE,∠BCF,∠BCD,∠ECF,∠ECD,∠FCD;
(2)以AB为一边的所有角有∠ABC,∠BAD,∠ABF;
(3)以F为顶点,FB为一边的所有角有∠AFB,∠BFC,∠BFD.
8.点O为直线AB上一点,将一直角三角板OMN的直角顶点放在点O处,射线OC平分∠MOB.
(1)如图1,若∠AOM=30°,求∠CON的度数;
(2)在图1中,若∠AOM=α,直接写出∠CON的度数(用含α的式子表示);
(3)将图1中的直角三角板OMN绕顶点O顺时针旋转至图2的位置,一边OM在直线AB上方,另一边ON在直线AB下方.
①探究∠AOM和∠CON的度数之间的关系,写出你的结论,并说明理由;
②当∠AOC=3∠BON时,求∠AOM的度数.
【解答】解:(1)由已知得∠BOM=180°﹣∠AOM=150°,
∵∠MON=90°,OC平分∠BOM,
∴∠CON=∠MON﹣∠BOM=90°﹣×150°=15°;
(2)由已知得∠BOM=180°﹣∠AOM=180°﹣a,
∵∠MON=90°,OC平分∠BOM,
∴∠CON=∠MON﹣∠BOM=90°﹣×(180°﹣a)=a;
(3)①设∠AOM=x,则∠BOM=180°﹣x,OC平分∠BOM,
∴∠MOC=∠BOM=(180°﹣x)=90°﹣,
∵∠MON=90°,
∴∠CON=∠MON﹣∠MOC=90°﹣(90°﹣x)=x,
∴∠CON=∠AOM;
②∵∠BON=∠MON﹣∠BOM=90°﹣(180°﹣x)=x﹣90°,
∴∠AOC=∠AOM+∠MOC=x+90°﹣=90°+x,
∵∠AOC=3∠BON,
∴90°+=3(x﹣90°),
解得x=144°,
∴∠AOM=144°.
9.如图,已知∠AOB是直角,射线OC在∠AOB的外面,OM,ON分别是∠AOC和∠BOC的平分线.
(1)若∠BOC=40°求∠MON的大小;
(2)当∠BOC=60°,其它条件不变时,直接写出∠MON的度数;
(3)写出∠MON与∠AOB之间的数量关系(∠BOC<90°).
【解答】解:(1)∵∠BOC=40°,ON是∠BOC的平分线,
∴∠NOC=∠BON=20°,
∵∠AOB是直角,
∴∠AOB=90°,
∴∠AOC=90°+40°=130°,
∵OM是∠AOC的平分线,
∴∠MOC=∠AOM=65°,
∴∠MON=∠MOC﹣∠NOC=65°﹣20°=45°;
(2)∵∠BOC=60°,ON是∠BOC的平分线,
∴∠NOC=∠BON=30°,
∵∠AOB是直角,
∴∠AOB=90°,
∴∠AOC=90°+60°=150°,
∵OM是∠AOC的平分线,
∴∠MOC=∠AOM=75°,
∴∠MON=∠MOC﹣∠NOC=75°﹣30°=45°;
(3)∠MON=∠AOB,
∵ON是∠BOC的平分线,
∴∠NOC=∠BOC,
∵∠AOB是直角,
∴∠AOB=90°,
∴∠AOC=90°+∠BOC,
∵OM是∠AOC的平分线,
∴∠MOC=∠AOC,
∴∠MON=∠MOC﹣∠NOC=∠AOC﹣∠BOC=(90°+∠BOC)﹣∠BOC=45°=∠AOB,
即∠MON=∠AOB.
10.如图,点C表示村庄,AC,BC是两条公路,AB是河流.点A和点B处各有一座小桥.已知:AC⊥BC,CD⊥AB.
(1)量出点C到河边的图上距离是 1.5 cm;
(2)如果此图按照1:10000的比例画出的,计算出C到河边的实地距离为多少m;
(3)如果测量队测出∠ABC=28°,求出∠FAE的度数.
【解答】解:(1)点C到AB的图上距离即线段CD的长度,测量可得点C到AB的图上距离是1.5厘米,
故答案为:1.5;
(2)1.5×10000=15000(厘米),
15000厘米=150米,
答:C到河边的实地距离为150米;
(3)∵AC⊥BC,∠ABC=28°,
∴∠BAC=90°﹣28°=62°,
∴∠EAF=∠BAC=62°.
11.已知:∠AOB=90°,直线CD过点O,OE平分∠AOD.
(1)如图1,当CD在∠AOB的外部时,若∠AOC=40°,则∠BOE= 20° ;
(2)如图2,当CD经过∠AOB的内部时,若∠AOC=150°,求∠BOE的度数;
(3)比较(1)(2),你有什么发现? ∠BOE=∠AOC. .
【解答】解:(1)∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∵∠AOC=40°,
∴∠DOB=50°,∠AOD=140°,
∵OE平分∠AOD,
∴∠DOE=∠AOD=70°,
∴∠BOE=∠DOE﹣∠DOB=70°﹣50°=20°.
故答案为:20°;
(2)∵∠AOC=150°,
∴∠AOD=30°,
∵OE平分∠AOD,
∴∠DOE=∠AOD=15°,
∵∠AOB=90°,
∴∠BOD=60°,
∴∠BOE=∠DOE+∠DOB=15°+60°=75°.
(3)∠BOE=∠AOC,
故答案为:∠BOE=∠AOC.
12.如图,用三张卡片拼成如图①,图②所示的两个四边形,其周长分别为C1、C2.
(1)请你根据所学知识解释:在直角三角形卡片中,“n<m”的理由是 垂线段最短 .
(2)分别计算C1、C2(用含m、n的代数式表示),并比较C1和C2的大小.
【解答】解:(1)在直角三角形卡片中,“n<m”的理由是垂线段最短,
故答案为:垂线段最短;
(2)如图所示,
C1=2m+4n;C2=4m+2n,
C1﹣C2=(2m+4n)﹣(4m+2n)=2n﹣2m=2(n﹣m),
∵n<m,
∴n﹣m<0,
∴2(n﹣m)<0,
∴C1<C2.
13.如图,点C在射线BE上,点F在线段AD上,CD平分∠FCE,∠FDC=∠FCD.
(1)当∠BAD=120°时,求∠ABC;
(2)点N是线段FD上一点,点P是线段CD上一点,连接AC,FP.若CA为∠BCF的角平分线,∠NCD=∠ACF,3∠BCN﹣2∠CFP=270°,探究直线CD上是否存在一点Q,使得FQ<FP.
【解答】解:(1)∵CD平分∠FCE,
∴∠DCF=∠DCE,
∵∠FDC=∠FCD,
∴∠FDC=∠DCE,
∴AD∥BE,
∴∠A+∠B=180°,
∵∠A=120°,
∴∠B=60°;
(2)∵CA为∠BCF的角平分线,
∴∠BCA=∠ACF,
∵∠BCA+∠ACF+∠DCF+∠DCE=180°,
∵∠DCF=∠DCE,
∴∠ACF+∠DCF=90°,
∴AC⊥CD,
设∠NCD=x,∠FCN=y,
∵∠NCD=∠ACF,
∴∠ACF=∠BCA=3x,
∵3∠BCN﹣2∠CFP=270°,
∴18x+3y+2∠CFP=270°①,
∵4x+y=90°②,
∴由①②消去y得∠CFP=3x,
∴∠CFP=∠ACF,
∴FP∥AC,
∴FP⊥CD,
∵垂线段最短,
∴直线CD上不存在一点Q,使得FQ<FP.
14.直线AB,CD相交于点O,OF⊥CD于点O,作射线OE,且OC在∠AOE的内部.
(1)①当OE、OF在如图1所示位置时,若∠BOD=20°,∠BOE=130°,求∠EOF的度数;
②当OE、OF在如图2所示位置时,若OF平分∠BOE,证明OC平分∠AOE.
(2)若∠AOF=2∠COE,请直接写出∠BOE与∠AOC之间的数量关系.
【解答】(1)①解:∵OF⊥CD于点O,
∴∠DOF=90°,
∵∠BOD=20°,
∴∠BOF=90°﹣20°=70°,
∵∠BOE=130°,
∴∠EOF=∠BOE﹣∠BOF=130°﹣70°=60°;
∴∠EOF的度数为60°;
②证明:∵OF平分∠BOE,
∴∠EOF=∠FOB=∠EOB,
∵OF⊥CD,
∴∠COF=90°,
∴∠COE+∠EOF=∠AOC+∠BOF=90°,
∴∠COE=∠AOC,即OC平分∠AOE;
(2)解:3∠AOC+2∠BOE=270°或∠AOC+2∠BOE=270°,
理由如下:
当点E,F在直线AB的同侧时,如图,
记∠COE=α,则∠AOF=2∠COE=2α,
∵OF⊥CD,
∴∠COF=90°,
∴∠EOF=90°﹣α,∠AOC=∠AOF﹣∠COF=2α﹣90°①,
∴∠BOE=180°﹣∠AOC﹣∠COE=180°﹣(2α﹣90°)﹣α=270°﹣3α②,
①×3+②×2得,3∠AOC+2∠BOE=270°;
当点E和点F在直线AB的异侧时,如图,
记∠COE=α,则∠AOF=2∠COE=2α,
∵OF⊥CD,
∴∠COF=90°,
∴∠AOC=∠COF﹣∠AOF=90°﹣2α①,
∴∠BOE=180°﹣∠AOC﹣∠COE=180°﹣(90°﹣2α)﹣α=90°+α②,
①+2×②得,∠AOC+2∠BOE=270°.
综上可知,3∠AOC+2∠BOE=270°或∠AOC+2∠BOE=270°.
15.如图,点C在线段AB上,AC<CB,点D、E分别是AB和CB的中点,AC=10cm,EB=8cm.
(1)求线段CD,DE,AB的长;
(2)是否存在点M,使它到A,C两点的距离之和等于8cm,为什么?
(3)是否存在点M,使它到A,C两点的距离之和大于10cm?如果点M存在,点M的位置应该在哪里?为什么?这样的点M有多少个?
【解答】解:(1)∵点E是CB的中点,EB=8cm,
∴CE=BE=8cm,
∴BC=CE+BE=8+8=16(cm),
∵AC=10cm,
∴AB=26cm,
∵点D是AB的中点,
∴AD=BD=13cm,
∴CD=AD﹣AC=13﹣10=3(cm),
DE=BD﹣BE=13﹣8=5(cm);
(2)不存在,
∵两点之间线段最短,
∴点A、C之间的最短距离为10cm,
故不存在点M,使它到A,C两点的距离之和等于8cm;
(3)存在,
∵两点之间线段最短,
∴线段AB外任何一点到A,C两点的距离之和都大于10cm,这样的点有无数个.
16.如图,是一个简单的平面示意图,已知OA=2km,OB=6km,OC=BD=4km,点E为OC的中点,回答下列问题:
(1)由图可知,高铁站在小明家南偏西65°方向6km处,请用类似的方法用方向与距离描述学校、博物馆相对于小明家的位置;
(2)图中到小明家距离相同的是哪些地方?
【解答】解:(1)由题意得:
90°﹣45°=45°,90°﹣40°=50°,
学校在小明家北偏东45°方向2km处,
博物馆在小明家南偏东50°方向4km处;
(2)∵OC=4km,点E为OC的中点,
∴OE=OC=2(km),
∵OB=6km,BD=4km,
∴OD=OB﹣BD=2(km),
∵OA=2km,
∴OA=OD=OE,
∴图中到小明家距离相同的是影院,公园,学校.
17.如图,已知点C在线段AB上,且AM=AC,BN=BC.
(1)若AC=12,CB=6,求线段MN的长.
(2)若C为线段AB上任意一点,且满足AC+BC=a,其他条件不变,求线段MN的长.
【解答】解:(1)∵AM=AC,
∴CM=AC,
∵AC=12,
∴CM=8,
∵BN=BC,
∴CN=BC,
∵BC=6,
∴CN=×6=4,
∴MN=CM+CN=8+4=12;
(2)∵AM=AC,BN=BC,
∴AM+BN=AC+BC=(AC+BC),
∴MN=MC+NC=(AC+BC),
∵AC+BC=a,
∴MN=a,
即线段MN的长为a.
18.已知射线OC在∠AOB的内部,若∠AOB,∠AOC和∠BOC三个角中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的奇妙线.
(1)一个角的平分线 是 这个角的奇妙线;(填“是”或“不是”)
(2)如图,∠MPN=60°.
①若射线PQ是∠MPN的奇妙线,则∠QPN的度数为 20或30或40 度;
②射线PF从PN位置开始,以每秒旋转3°45'的速度绕点P按逆时针方向旋转,当
∠FPN首次等于180°时停止旋转,设旋转的时间为t(s).当t为何值时,射线PM是∠FPN的奇妙线?
【解答】解:(1)一个角的平分线是这个角的“奇妙线”;
故答案为:是.
(2)①若∠MPN=60°,且射线PQ是∠MPN的“奇妙线”,则由“奇妙线”的定义可知有三种情况符合题意:
当∠NPQ=2∠MPQ时,∠QPN=40°,
当∠MPQ=2∠NPQ时,∠QPN=20°,
当∠NPM=2∠MPQ时,∠QPN=30°,
故答案为:20或30或40;
②依题意有,3°45′=3.75°,
当3.75t=60+×60时,
解得t=24;
当3.75t=2×60时,
解得t=32;
当3.75t=60+2×60时,
解得t=48.
故当t为24或32或48时,射线PM是∠FPN的“奇妙线”;
19.在平面直角坐标系中,D(0,﹣3),M(4,﹣3),直角三角形ABC的边与x轴分别相交于O、G两点,与直线DM分别交于E、F点,∠ACB=90°.
(1)将直角三角形如图1位置摆放,如果∠AOG=46°,则∠CEF= 136° ;
(2)将直角三角形ABC如图2位置摆放,N为AC上一点,
①若∠NEC+∠CEF=180°,请直接写出∠NEF与∠AOG之间的等量关系: ∠NEF=2∠AOG ;
②若∠NED+∠CEF=180°,请判断∠NEF与∠AOG之间的等量关系,并说明理由.
(3)将直角三角形ABC如图3位置摆放,若∠GOC=140°,延长AC交DM于点Q,点P是射线GF上一动点,探究∠POQ,∠OPQ与∠PQF的数量关系,请直接写出结论(题中的所有角都大于0°小于180°): OPQ=140°﹣∠POQ+∠PQF或140°﹣∠POQ=∠OPQ+∠PQF .
【解答】解:(1)过点C作CP∥DM,
∵D(0,﹣3),M(4,﹣3),
∴DM∥x轴,
∴CP∥DM∥x轴,
∴∠AOG=∠ACP,∠BCP+∠CEF=180°,
∴∠BCP=180°﹣∠CEF,
∵∠ACP+∠BCP=90°,
∴∠AOG+180°﹣∠CEF=90°,
∵∠AOG=46°,
∴∠CEF=136°.
故答案为:136°.
(2)①过点C作CQ∥x轴,
∴CQ∥EM∥x轴,
∴∠AOG=∠ACQ,∠ECQ=∠CEK,
∵∠NEC+∠CEF=180°,∠CEK+∠CEF=180°,
∴∠NEC=∠CEK,
∵∠ACQ+∠ECQ=90°,
∴∠ECQ=∠CEK=∠NEC=90°﹣∠ACQ=90°﹣∠AOG,
∵∠CEK+∠NEC+∠NEF=180°,
∴2(90°﹣∠AOG)+∠NEF=180°,
整理得∠NEF=2∠AOG.
故答案为:∠NEF=2∠AOG.
②∠NEF+∠AOG=90°.
理由如下:
∵CQ∥EM∥x轴,
∴∠AOG=∠ACQ,∠ECQ=∠CEK,
∵∠NED+∠CEF=180°,∠CEK+∠CEF=180°,
∴∠NED=∠CEK,
∵∠ACQ+∠ECQ=90°,
∴∠AOG+∠NEF=90°.
(3)当点P在GF上时,过点P作PH∥OG,
∴PH∥OG∥DM,
∴∠GOP=∠OPH,∠PQF=∠HPQ,
∴∠OPQ=∠GOP+∠PQF,
∴∠OPQ=140°﹣∠POQ+∠PQF.
当点P在线段GF的延长线上时,
∴PR∥OG∥DM,
∴∠GOP=∠OPR,∠PQF=∠QPR,
∵∠OPR=∠OPQ+∠QPR,
∴∠GOP=∠OPQ+∠PQF,
∴140°﹣∠POQ=∠OPQ+∠PQF.
故答案为:∠OPQ=140°﹣∠POQ+∠PQF或140°﹣∠POQ=∠OPQ+∠PQF.
20.以直线AB上一点O为端点作射线OC,使∠BOC=30°,将一个直角三角板的直角顶点放在O处,即∠DOE=90°.
(1)如图1,若直角三角板DOE的一边OE放在射线OA上,则∠COD= 60° ;
(2)如图2,将直角三角板DOE绕点O顺时针转动到某个位置,
①若OE恰好平分∠AOC,则∠COD= 15° ;
②若OD在∠BOC内部,请直接写由∠BOD与∠COE的数量关系为 ∠COE=∠BOD+30° ;
(3)将直角三角板DOE绕点O顺时针转动(与OB重合时为停止)的过程中,恰好有∠COD=∠AOE,求此时∠BOD的度数.
【解答】解:(1)∵∠BOD=90°,∠BOC=30°,
∴∠COD=∠BOD﹣∠BOC=90°﹣30°=60°.
故答案为:60°;
(2)①∵∠AOC=∠AOD+∠COD,
∴∠AOC=90°+60°=150°,
∵OE平分∠AOC,
∴,
∴∠COD=90°﹣∠COE=90°﹣75°=15°;
故答案为:15°;
②∵∠COE+∠COD=90°,
∠BOD+∠COD=30°,
∴∠COD=∠BOD+30°;
故答案为:∠COD=∠BOD+30°;
(3)∵∠COD+∠COE=90°,∠COE+∠AOE=150°,
∴∠AOE=60°+∠COD,
∵∠COD=∠AOE,
∴∠COD=15°,
∴∠BOD=∠BOC﹣∠COD=30°﹣15°=15°.
21.如图,O是直线EF上一点,OD是直线EF上方过点O的一条射线,∠DOE=70°,若射线OA在∠DOF的内部,∠AOD的度数为x(x<36°).射线OB在直线EF上方,且∠BOE=5∠AOD.
(1)∠AOE= x+70° (x的代数式表示);
(2)当∠AOB=30°时,求x的值;
(3)若射线OC在∠AOE的内部,且∠COE=4∠AOD,当OA,OB,OC三条射线中的一条射线是另外两条射线组成的夹角的平分线时,请直接写出x的值.
【解答】解:(1)∠AOE=x+70°.
故答案为:x+70°;
(2)①当射线OB在OA左边时,
∵∠BOE=5∠AOD,∠AOB=30°,∠AOD的度数为x(x<36°).
∴∠AOB=∠AOE﹣∠BOE,
∴70°+x﹣5x=30°,解得x=10°;
②当射线OB在OA右边时,
∵∠BOE=5∠AOD,∠AOB=30°,∠AOD的度数为x(x<36°).
∴∠AOB=∠BOE﹣∠AOE,
∴5x﹣70°﹣x=30°,解得x=25°;
综上,x的值为10或25;
(3)x的值为14,20,35.
∵∠COE=4∠AOD=4x,∠BOE=5∠AOD=5x.
∴∠COE<∠BOE,
∴射线OC在OB的左边,
①当OB为∠AOC的平分线时,
∵∠AOB=∠AOE﹣∠BOE=70°+x﹣5x=70°﹣4x,
∠BOC=∠BOE﹣∠COE=5x﹣4x=x,
∴70°﹣4x=x,
解得:x=14°;
②当OA为∠BOC的平分线时,
∵∠AOB=∠BOE﹣∠AOE=5x﹣70°﹣x=4x﹣70°,
∠AOC=∠AOE﹣∠COE=70°+x﹣4x=70°﹣3x,
∴4x﹣70°=70°﹣3x,
解得:x=20°;
综上,满足条件的x的值为14,20,35.
22.如图,将正方形纸片ABCD折叠,使点D落在BC边点E处,点A落在点F处,折痕为MN,若∠NEC=32°,求∠FMN的大小.
【解答】解:∵四边形ABCD是正方形,正方形纸片ABCD折叠,使点D落在BC边点E处,点A落在点F处,
∴∠F=∠A=90°,∠DNM=∠ENM,∠FEN=∠D=90°,
∵∠NEC=32°,
∴∠ENC=90°﹣32°=58°,
∴,
∴∠FMN=360°﹣90°﹣90°﹣61°=119°.
23.已知点O是直线AB上一点,过O作射线OC,使∠BOC=110°.
(1)如图1,∠AOC的度数是 70° ;
(2)如图2,过点O作射线OD使∠COD=90°,作∠AOC的平分线OE,求∠DOE的度数.
(3)在(2)的条件下,作射线OF,若∠BOF与∠AOE互余,请直接写出∠DOF的度数.
【解答】解:(1)∵∠AOC+∠BOC=180°,∠BOC=110°,
∴∠AOC=180°﹣110°=70°,
故答案为:70°;
(2)∵OE是∠AOC的平分线,
∴∠AOE=∠COE=∠AOC=35°,
又∵∠COD=90°,
∴∠DOE=∠COE+∠COD=125°;
(3)由(2)得∠AOE=35°,∠BOD=110°﹣90°=20°,
∵∠BOF与∠AOE互余,
∴∠BOF=90°﹣35°=55°,
①当射线OF在射线OB的上方时,有∠DOF=∠BOF﹣∠BOD=55°﹣20°=35°,
②当射线OF在射线OB的下方时,有∠DOF=∠BOF+∠BOD=55°+20°=75°,
答:∠DOF的度数为35°或75°.
24.如图,直线AB,CD相交于点O,OB平分∠DOE,
(1)如图1,若∠COE=110°,求∠BOD的度数
(2)如图2,若∠BOE:∠COE=1:3,求∠AOC的度数;
(3)在(2)的条件下,画OF⊥CD,请直接写出∠EOF的度数.
【解答】解:(1)∵∠COE+∠DOE=180°,∠COE=110°,
∴∠DOE=180°﹣110°=70°,
又∵OB平分∠DOE,
∴∠BOD=∠BOE=∠DOE=35°;
(2)∵OB平分∠DOE,
∴∠BOD=∠BOE=∠DOE,
∵∠BOE:∠COE=1:3,
∴∠BOD=180°×=36°,
∴∠AOC=∠BOD=36°;
(3)由(2)得∠DOE=72°,
当OF在直线CD的上方时,有∠EOF=∠FOD+∠DOE=90°+72°=162°,
当OF在直线CD的下方时,有∠EOF=∠FOD﹣∠DOE=90°﹣72°=18°,
因此∠EOF的度数为18°或162°.
