相似三角形的判定定理2[下学期]
文档属性
| 名称 | 相似三角形的判定定理2[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 36.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-21 00:00:00 | ||
图片预览


文档简介
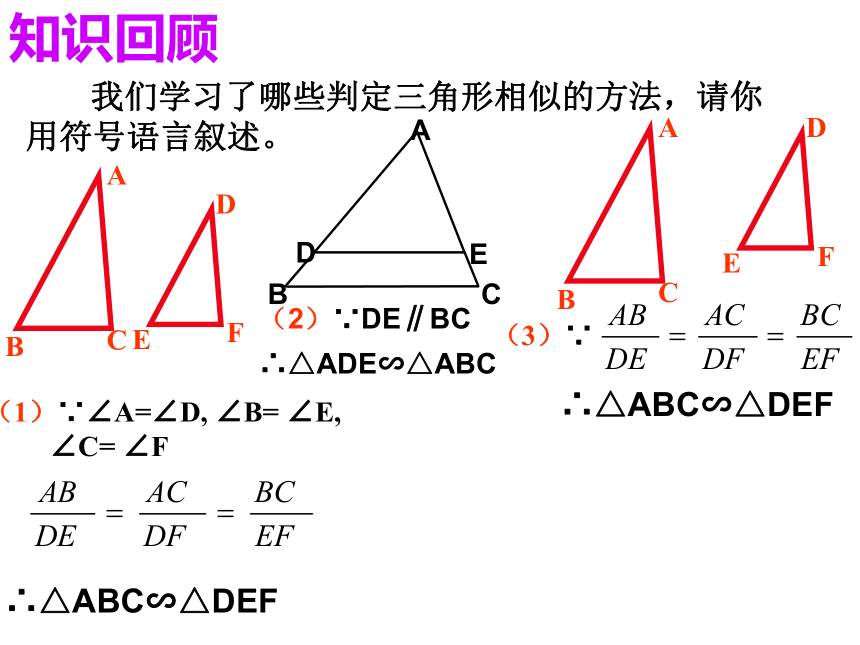
课件12张PPT。相似三角形的判定定理2(2)∵DE∥BC
∴△ADE∽△ABC 我们学习了哪些判定三角形相似的方法,请你用符号语言叙述。知识回顾(1)∵∠A=∠D, ∠B= ∠E,
∠C= ∠F∴△ABC∽△DEF(3)∵∴△ABC∽△DEF判定定理2:如果两个三角形的两组对应边的比
相等,并且相应的夹角相等,
那么这两个三角形相似 由三角形全等的判定定理(SAS)
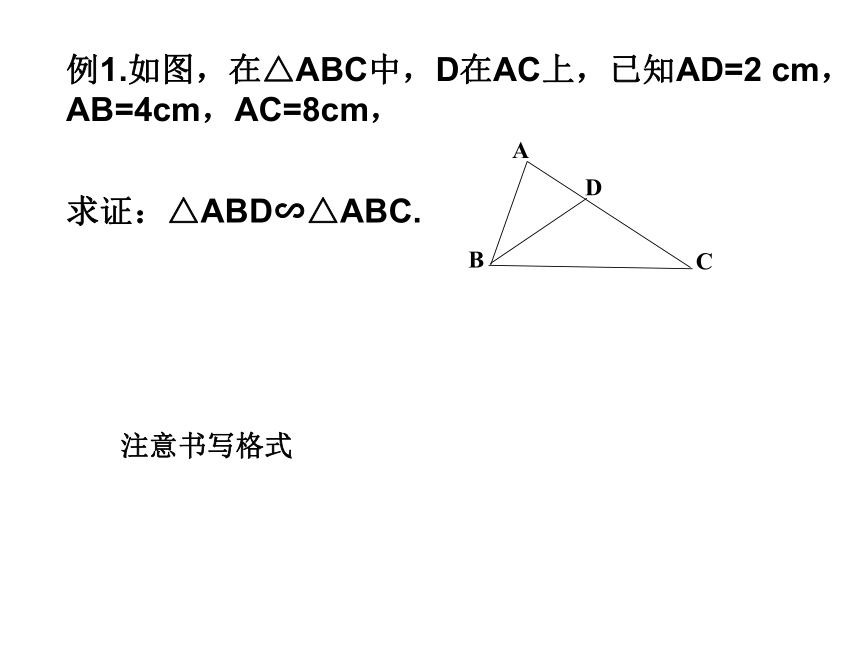
猜想得出相似的判定定理2∠A=∠D求证:△ABC∽△DEF 已知在△ABC 和△DEF中,例1.如图,在△ABC中,D在AC上,已知AD=2 cm,
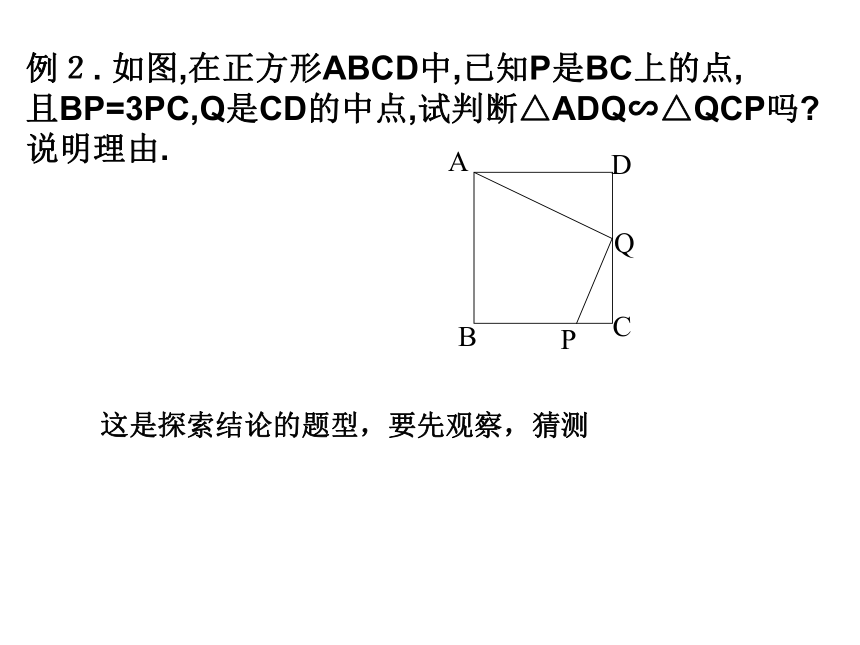
AB=4cm,AC=8cm, 求证:△ABD∽△ABC. 注意书写格式例2. 如图,在正方形ABCD中,已知P是BC上的点,
且BP=3PC,Q是CD的中点,试判断△ADQ∽△QCP吗?
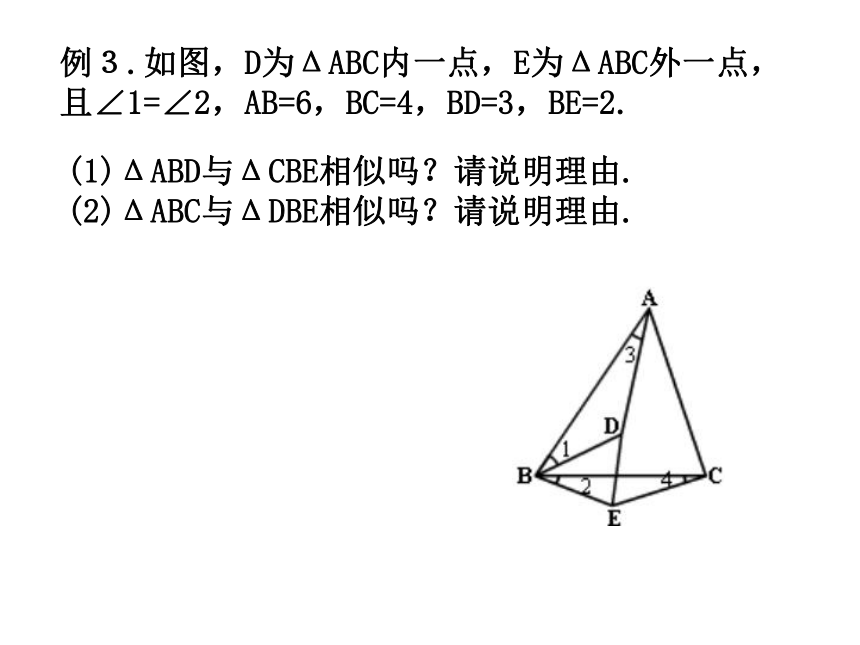
说明理由.这是探索结论的题型,要先观察,猜测例3.如图,D为ΔABC内一点,E为ΔABC外一点,
且∠1=∠2,AB=6,BC=4,BD=3,BE=2.
(1)ΔABD与ΔCBE相似吗?请说明理由.
(2)ΔABC与ΔDBE相似吗?请说明理由.
1.如下图所示,在△ABC中,D﹑E分别在AC﹑AB上,
且AD:AB=AE:AC=1:2,BC=5,则DE=________ 练一练2.如图,在4×4的正方形方格中,△ABC和△DEF
的顶点都在边长为1的小正方形的顶点上.
(1)填空:∠ABC= °,BC= ;
(2)判断△ABC与△DEF是否相似,并证明你的结论.3.如图,在正方形网格上有6个斜三角形:①△ABC
②△BCD;③△BDE;④△BFG;⑤△FGH;⑥△EKF。
其中②~⑥中与三角形①相似的三角形是_____________K4.已知零件的外径为25cm,要求它的厚度x,
需先求出它的内孔直径AB,现用一个交叉卡钳
(AC和BD的长相等)去量(如图),
若OA:OC=OB:OD=3,CD=7cm。求此零件的厚度x。注意审题,题中没有平行条件5.如图,Rt△ABC,D、E是BC上两点,
且AB=BD=DE=EC,请问:此图中共有几个三角形?
是否存在相似三角形?如果有请你指出来,并加以证明.6.已知,如图,O点在△ABC内部,连AO、BO、CO,
A’、B’、C’分别在AO、BO、CO上,且AB∥A’B’、
BC∥B’C’.⑴求证:△OAC∽△OA’C’.
⑵若将图⑴中的O点移至△ABC外,如图,
其它条件不变,题中要求证的结论成立吗?
①在图⑵基础上画出相应的图形,观察并回答
答: (填成立或不成立).
②证明你在①中观察到的结论.A′C′B′思考还有其它的结论吗?本节课你有什么收获?
∴△ADE∽△ABC 我们学习了哪些判定三角形相似的方法,请你用符号语言叙述。知识回顾(1)∵∠A=∠D, ∠B= ∠E,
∠C= ∠F∴△ABC∽△DEF(3)∵∴△ABC∽△DEF判定定理2:如果两个三角形的两组对应边的比
相等,并且相应的夹角相等,
那么这两个三角形相似 由三角形全等的判定定理(SAS)
猜想得出相似的判定定理2∠A=∠D求证:△ABC∽△DEF 已知在△ABC 和△DEF中,例1.如图,在△ABC中,D在AC上,已知AD=2 cm,
AB=4cm,AC=8cm, 求证:△ABD∽△ABC. 注意书写格式例2. 如图,在正方形ABCD中,已知P是BC上的点,
且BP=3PC,Q是CD的中点,试判断△ADQ∽△QCP吗?
说明理由.这是探索结论的题型,要先观察,猜测例3.如图,D为ΔABC内一点,E为ΔABC外一点,
且∠1=∠2,AB=6,BC=4,BD=3,BE=2.
(1)ΔABD与ΔCBE相似吗?请说明理由.
(2)ΔABC与ΔDBE相似吗?请说明理由.
1.如下图所示,在△ABC中,D﹑E分别在AC﹑AB上,
且AD:AB=AE:AC=1:2,BC=5,则DE=________ 练一练2.如图,在4×4的正方形方格中,△ABC和△DEF
的顶点都在边长为1的小正方形的顶点上.
(1)填空:∠ABC= °,BC= ;
(2)判断△ABC与△DEF是否相似,并证明你的结论.3.如图,在正方形网格上有6个斜三角形:①△ABC
②△BCD;③△BDE;④△BFG;⑤△FGH;⑥△EKF。
其中②~⑥中与三角形①相似的三角形是_____________K4.已知零件的外径为25cm,要求它的厚度x,
需先求出它的内孔直径AB,现用一个交叉卡钳
(AC和BD的长相等)去量(如图),
若OA:OC=OB:OD=3,CD=7cm。求此零件的厚度x。注意审题,题中没有平行条件5.如图,Rt△ABC,D、E是BC上两点,
且AB=BD=DE=EC,请问:此图中共有几个三角形?
是否存在相似三角形?如果有请你指出来,并加以证明.6.已知,如图,O点在△ABC内部,连AO、BO、CO,
A’、B’、C’分别在AO、BO、CO上,且AB∥A’B’、
BC∥B’C’.⑴求证:△OAC∽△OA’C’.
⑵若将图⑴中的O点移至△ABC外,如图,
其它条件不变,题中要求证的结论成立吗?
①在图⑵基础上画出相应的图形,观察并回答
答: (填成立或不成立).
②证明你在①中观察到的结论.A′C′B′思考还有其它的结论吗?本节课你有什么收获?
