27.2相似三角形判定一习题课[下学期]
文档属性
| 名称 | 27.2相似三角形判定一习题课[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 356.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-22 00:00:00 | ||
图片预览




文档简介
课件15张PPT。27.2.1 相似三角形的判定习题课1.判断题
⑴两个菱形是相似形. ( )
⑵两个矩形是相似形. ( )
⑶两个正方形是相似形. ( )
⑷两个正多边形是相似形. ( )
⑸有一个角相等的两个等腰梯形是相似形.( )
⑹两个直角梯形是相似形. ( )2.下列说法正确的是( )
A.相似形是全等形. B.全等形是相似形.
C.不全等的图形不是相似形.
D.不相似的图形可能是全等形.牛刀小试:3.下列各组图形中,肯定是相似形的是( ).
A.两个腰长不相等的等腰三角形
B.两个半径不等的圆
C.两个面积不相等的平行四边形
D.两个面积不相等的菱形4.下列图形中,必是相似形的是( )
A.都有一个角是40o的两个等腰三角形
B.都有一个角为50o的两个等腰梯形
C.都有一个角是30o的两个菱形
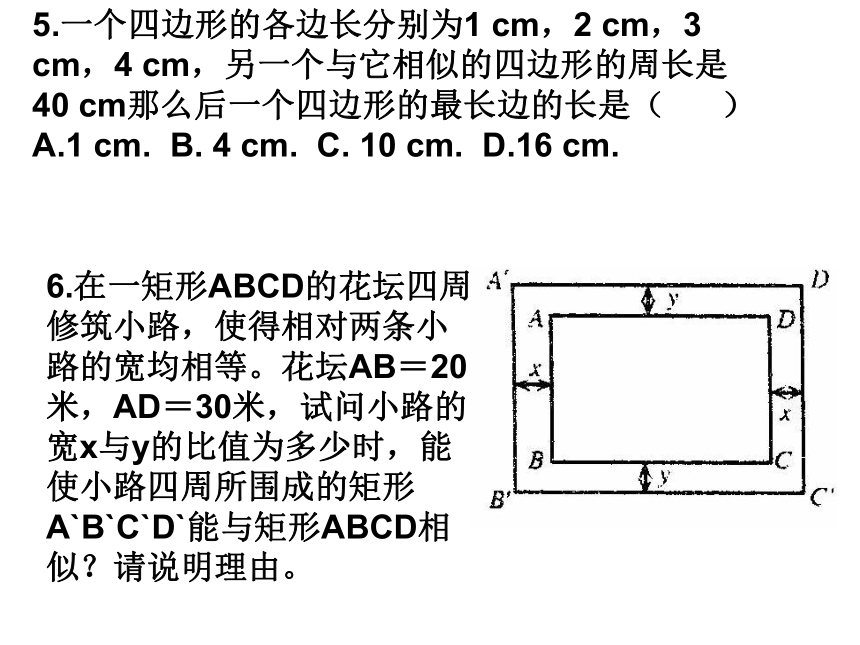
D.邻边之比为2:3的两个平行四边形.牛刀小试:5.一个四边形的各边长分别为1 cm,2 cm,3 cm,4 cm,另一个与它相似的四边形的周长是40 cm那么后一个四边形的最长边的长是( )
A.1 cm. B. 4 cm. C. 10 cm. D.16 cm.6.在一矩形ABCD的花坛四周修筑小路,使得相对两条小路的宽均相等。花坛AB=20米,AD=30米,试问小路的宽x与y的比值为多少时,能使小路四周所围成的矩形A`B`C`D`能与矩形ABCD相似?请说明理由。 牛刀小试:7.根据下列条件判断△ABC与△DEF是否相似。(1)AB=3,BC=4,AC=6;
DE=6,EF=8,DF=12(3)AB=3,BC=4,AC=6;
DE=6,EF=9,DF=12(2)AB=3,BC=4,AC=6;
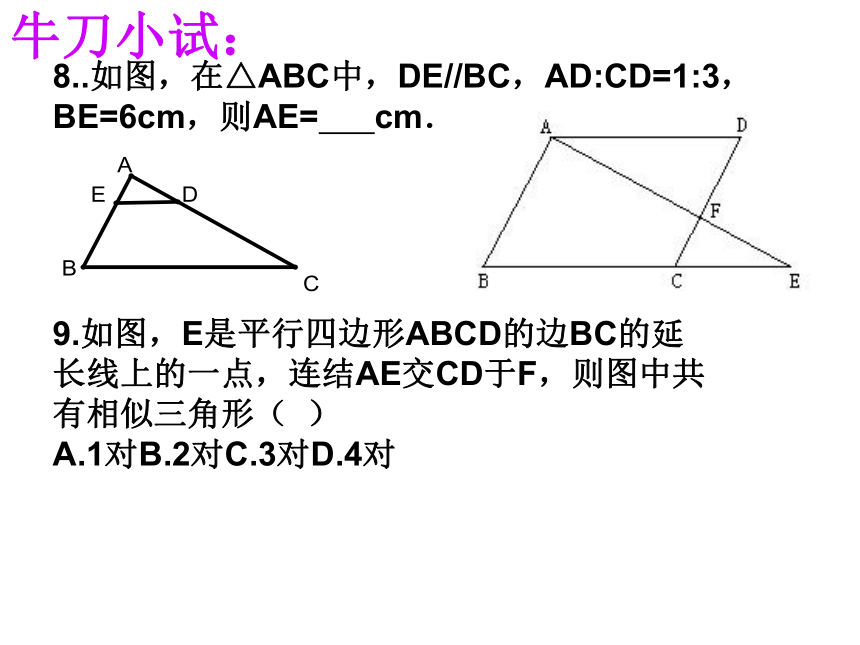
DE=6,EF=12,DF=8△ABC∽△DEF△ABC∽不 相 似△EDF8..如图,在△ABC中,DE//BC,AD:CD=1:3,BE=6cm,则AE= cm.9.如图,E是平行四边形ABCD的边BC的延长线上的一点,连结AE交CD于F,则图中共有相似三角形( )
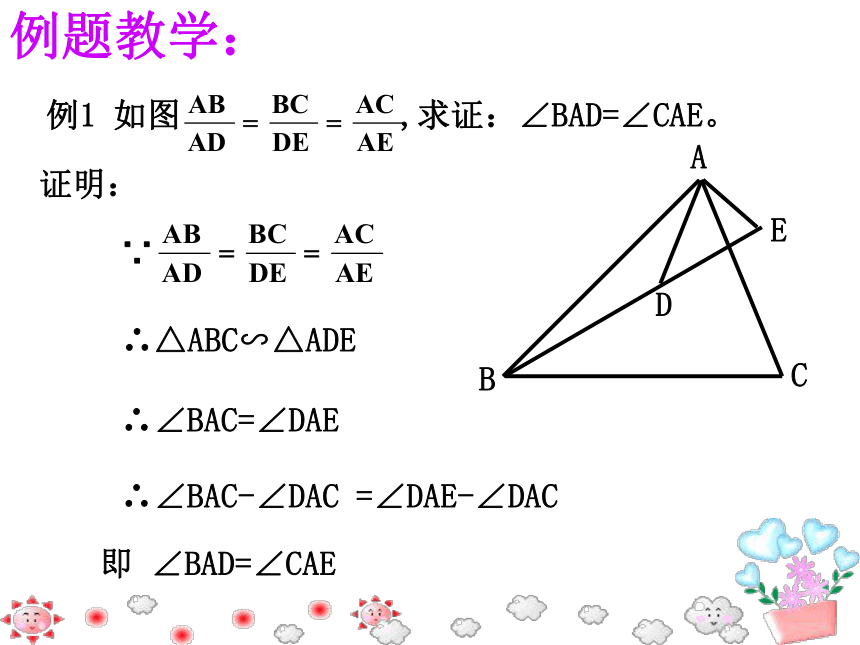
A.1对 B.2对 C.3对 D.4对牛刀小试:例题教学:证明:即 ∠BAD=∠CAE∵∴△ABC∽△ADE∴∠BAC=∠DAE∴∠BAC-∠DAC =∠DAE-∠DAC 2.如图,在□ABCD中,E、F分别是AB、BC的中点,连接AC、EF.求证:△BEF∽△ACD.例题教学:∴△BDM∽△BCA解:∵MD∥AC,又∵ ME∥AB,∴△CEM∽△CAB3份巩固练习:练2 如图,△ABC中,AB=12,AC=8,AE=4,请在AB上找到一点D,使△ADE与△ABC相似,并求AD边的长。巩固练习:解:(1)过点E作ED∥BC交AC于点D。∴△AED∽△ABC∵ DE∥BC∴(2)如图在AC上取点D′,连结ED ′,若:∴△AED′∽△ACBAD′=61.如图,物AB与其所成像A’B’平行,孔心O到蜡烛头A的距离是36cm,到蜡烛头的像A’的距离是12cm,你知道像长是物长的几分之几吗?你是怎样知道的?学以致用2.如图:一条河流,在河流的北岸点A处有一根高压电线杆。河流的南岸点B处有一颗大树。且电线杆在大树的正北方向上。在大树的正东方的点C处有一雕像,你能利用本节课学习的知识大致测算出电线杆A与大树B之间的距离吗? 若用皮尺测得:BC=50米,CD=20米,DE=60米,你能计算出电线杆A与大树B之间的距离吗?ABCDE学以致用1、如图: ABCD,E是AB延长线上一点。DE与AC和BC分别相交于点O、F。你能找出图中的相似三角形吗?并说明理由。巩固提高:G2.如图,在□ABCD中,已知E是AB的中点,在AD上截取AF=FD,EF交AC于G,求 的值. 巩固提高:再 见!
⑴两个菱形是相似形. ( )
⑵两个矩形是相似形. ( )
⑶两个正方形是相似形. ( )
⑷两个正多边形是相似形. ( )
⑸有一个角相等的两个等腰梯形是相似形.( )
⑹两个直角梯形是相似形. ( )2.下列说法正确的是( )
A.相似形是全等形. B.全等形是相似形.
C.不全等的图形不是相似形.
D.不相似的图形可能是全等形.牛刀小试:3.下列各组图形中,肯定是相似形的是( ).
A.两个腰长不相等的等腰三角形
B.两个半径不等的圆
C.两个面积不相等的平行四边形
D.两个面积不相等的菱形4.下列图形中,必是相似形的是( )
A.都有一个角是40o的两个等腰三角形
B.都有一个角为50o的两个等腰梯形
C.都有一个角是30o的两个菱形
D.邻边之比为2:3的两个平行四边形.牛刀小试:5.一个四边形的各边长分别为1 cm,2 cm,3 cm,4 cm,另一个与它相似的四边形的周长是40 cm那么后一个四边形的最长边的长是( )
A.1 cm. B. 4 cm. C. 10 cm. D.16 cm.6.在一矩形ABCD的花坛四周修筑小路,使得相对两条小路的宽均相等。花坛AB=20米,AD=30米,试问小路的宽x与y的比值为多少时,能使小路四周所围成的矩形A`B`C`D`能与矩形ABCD相似?请说明理由。 牛刀小试:7.根据下列条件判断△ABC与△DEF是否相似。(1)AB=3,BC=4,AC=6;
DE=6,EF=8,DF=12(3)AB=3,BC=4,AC=6;
DE=6,EF=9,DF=12(2)AB=3,BC=4,AC=6;
DE=6,EF=12,DF=8△ABC∽△DEF△ABC∽不 相 似△EDF8..如图,在△ABC中,DE//BC,AD:CD=1:3,BE=6cm,则AE= cm.9.如图,E是平行四边形ABCD的边BC的延长线上的一点,连结AE交CD于F,则图中共有相似三角形( )
A.1对 B.2对 C.3对 D.4对牛刀小试:例题教学:证明:即 ∠BAD=∠CAE∵∴△ABC∽△ADE∴∠BAC=∠DAE∴∠BAC-∠DAC =∠DAE-∠DAC 2.如图,在□ABCD中,E、F分别是AB、BC的中点,连接AC、EF.求证:△BEF∽△ACD.例题教学:∴△BDM∽△BCA解:∵MD∥AC,又∵ ME∥AB,∴△CEM∽△CAB3份巩固练习:练2 如图,△ABC中,AB=12,AC=8,AE=4,请在AB上找到一点D,使△ADE与△ABC相似,并求AD边的长。巩固练习:解:(1)过点E作ED∥BC交AC于点D。∴△AED∽△ABC∵ DE∥BC∴(2)如图在AC上取点D′,连结ED ′,若:∴△AED′∽△ACBAD′=61.如图,物AB与其所成像A’B’平行,孔心O到蜡烛头A的距离是36cm,到蜡烛头的像A’的距离是12cm,你知道像长是物长的几分之几吗?你是怎样知道的?学以致用2.如图:一条河流,在河流的北岸点A处有一根高压电线杆。河流的南岸点B处有一颗大树。且电线杆在大树的正北方向上。在大树的正东方的点C处有一雕像,你能利用本节课学习的知识大致测算出电线杆A与大树B之间的距离吗? 若用皮尺测得:BC=50米,CD=20米,DE=60米,你能计算出电线杆A与大树B之间的距离吗?ABCDE学以致用1、如图: ABCD,E是AB延长线上一点。DE与AC和BC分别相交于点O、F。你能找出图中的相似三角形吗?并说明理由。巩固提高:G2.如图,在□ABCD中,已知E是AB的中点,在AD上截取AF=FD,EF交AC于G,求 的值. 巩固提高:再 见!
