27.2.1相似三角形的判定(2)[下学期]
文档属性
| 名称 | 27.2.1相似三角形的判定(2)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 298.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-22 22:31:00 | ||
图片预览






文档简介
课件24张PPT。 玉环实验学校 27.2.1相似三角形的判定(2)一 温故知新判定三角形相似的方法判定两个三角形相似的方法之一:
平行于三角形一边的直线和其他两边相交(或两边的延长线相交 ) 所构成的三角形与原三角形相似.
这是两个极具代表性的相似三角形
基本模型:“A”型和“Z” 型
类比三角形全等的判定方法:
边边边(SSS);边角边(SAS);角边角(ASA);角角边(AAS); 斜边直角边(HL).
你能否得出判定三角形相似的其它方法?二 探究新知相似与全等 类比—新化旧三角形全等的判定方法:
边边边(SSS);边角边(SAS);角边角(ASA);角角边(AAS); 斜边直角边(HL).
由边边边(SSS)可猜想:
三边对应成比例的两个三角形相似;
由边角边(SAS)可猜想:
两边对应成比例,且夹角相等的两个三角形相似;由角边角(ASA);角角边(AAS)可猜想:两个角对应相等的两个三角形相似;
由斜边直角边(HL)可猜想:
斜边直角边对应成比例的两个直角三角形相似.
如何把我们的猜想变为现实?(证明)问题一:
如果△ ABC与△ A′B′C′三边对应成比例,那么它们一定相似吗?我们一起来动手:
画△ ABC与△ A′B′C′,设法比较∠A与∠A′的大小, ∠B与∠B′的大小,∠C与∠C′的大小.
△ ABC与△ A′B′C′相似吗?说说你的理由.
改变k值的大小(如1∶3),再试一试.
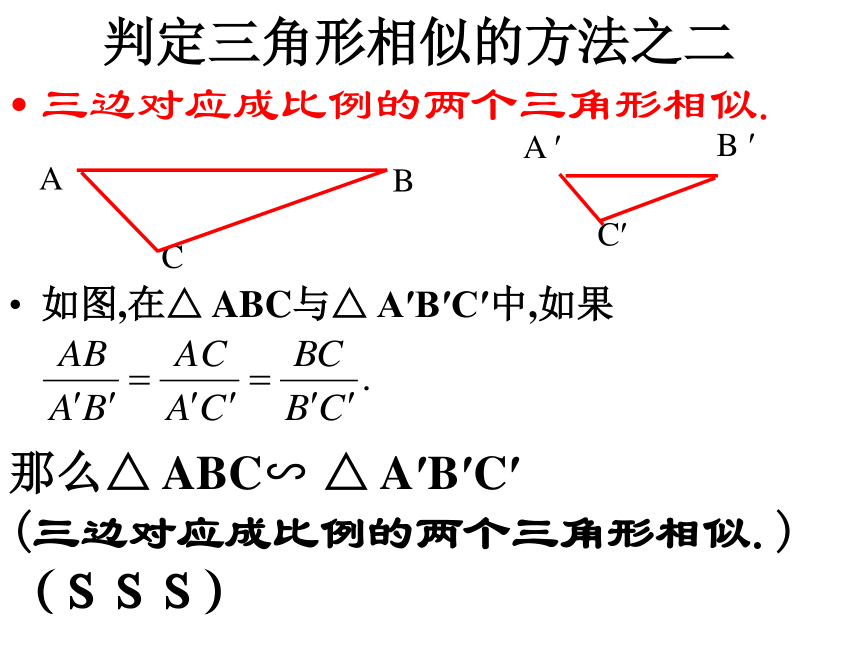
通过上面的活动,你猜出了什么结论?判定三角形相似的方法之二三边对应成比例的两个三角形相似.如图,在△ ABC与△ A′B′C′中,如果那么△ ABC∽ △ A′B′C′
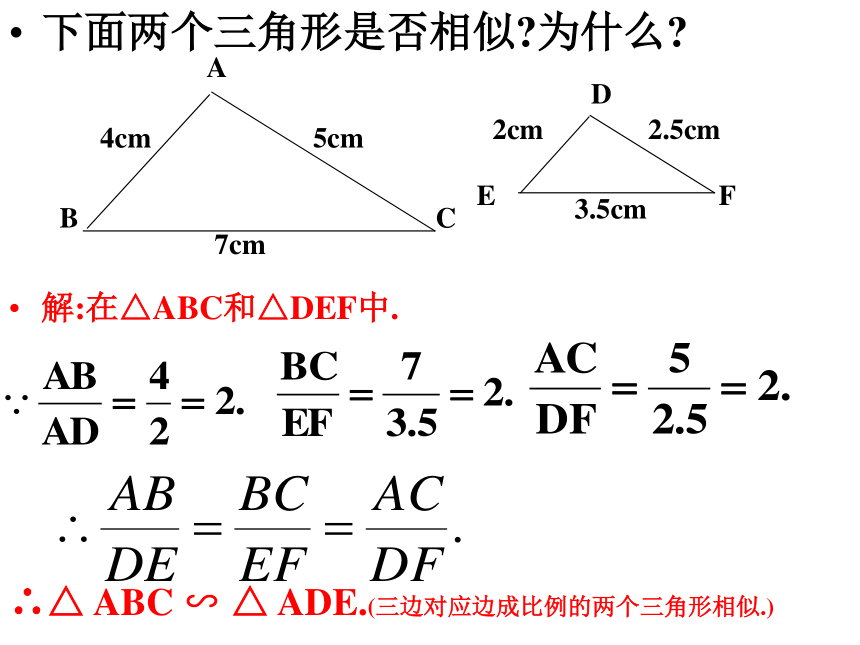
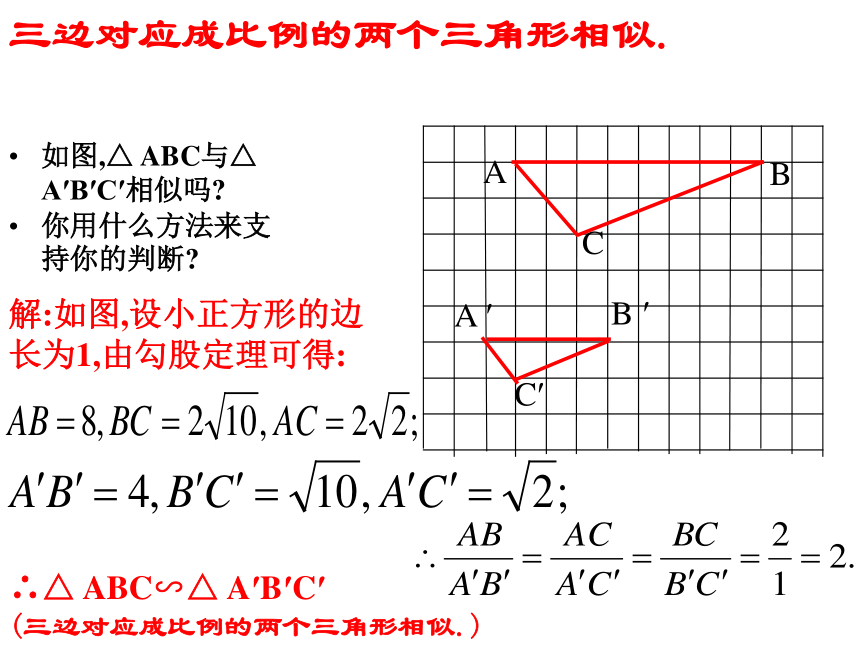
(三边对应成比例的两个三角形相似.)(SSS)下面两个三角形是否相似?为什么?解:在△ABC和△DEF中.∴△ ABC ∽ △ ADE.(三边对应边成比例的两个三角形相似.)三边对应成比例的两个三角形相似.如图,△ ABC与△ A′B′C′相似吗?
你用什么方法来支持你的判断?∴△ ABC∽△ A′B′C′
(三边对应成比例的两个三角形相似.)解:如图,设小正方形的边长为1,由勾股定理可得:问题二:
如果△ ABC与△ A′B′C′两边对应成比例,且这两边的夹角相等.那么它们一定相似吗?我们一起来动手:
画△ ABC与△ A′B′C′,设法比较它们的第三组对应边BC和B′C′的大小, 它们的比等于K吗?
△ ABC与△ A′B′C′相似吗?说说你的理由.
改变k值或∠A的大小再试一试.
通过上面的活动,你猜出了什么结论?判定三角形相似的方法之三两边对应成比例,并且相应的夹角相等,这两个三角形相似.如图,在△ ABC与△ A′B′C′中,如果那么△ ABC∽ △ A′B′C′
(两边对应成比例且夹角相等的两个三角形相似.)(SAS)例 如图矩形ABCD是由三个正方形ABEG,GEFH,HFCD组成的,找出图中的相似三角形.解:△ AEF∽ △CEA.理由是:
设小正方形的边长是1,由勾股定理得∴△ AEF ∽ △CEA.
(三边对应边成比例的两个三角形相似.)∴△ AEF ∽ △CEA.
(两条对应边成比例且它们的夹角对应相等的两个三角形相似.)∵∠ AEF = ∠CEA=135°. 上述判定方法中的“角”一定是两对应边的夹角吗?三 同步训练你掌握了吗?四 思维拓展★ 探讨了相似三角形的另两种判定方法:★ 数学活动充满着探索与创新,请同学们利用所学知识解决生活中的实际问题. 如图,△ABC与△ A’ B’ C’ 相似吗?你有哪些判断方法?试试你的能力 有一池塘, 周围都是空地. 如果要测量池塘两端A、B间的距离, 你能利用本节所学的知识解决这个问题吗???AB △ABC的顶点A、B、C在单位正方形的顶点上 ,请在图中画一个△A1B1C1 使
△ A1B1C1 ∽△ABC
(相似比不为1),
且点都在单位正方形
的顶点上 . 在正方形方格中,CAB五 课时小结判定三角形相似的常用方法:
三边对应成比例的两个三角形相似.
两边对应成比例并且夹角相等的两个三角形相似.
相似三角形的各对应角相等,各对应边对应成比例.那么△ ABC∽ △DEF.那么△ ABC∽ △结束寄语可以用一次的想法是一个决窍,如果它可以用两次以上,那就成为一种方法了.
平行于三角形一边的直线和其他两边相交(或两边的延长线相交 ) 所构成的三角形与原三角形相似.
这是两个极具代表性的相似三角形
基本模型:“A”型和“Z” 型
类比三角形全等的判定方法:
边边边(SSS);边角边(SAS);角边角(ASA);角角边(AAS); 斜边直角边(HL).
你能否得出判定三角形相似的其它方法?二 探究新知相似与全等 类比—新化旧三角形全等的判定方法:
边边边(SSS);边角边(SAS);角边角(ASA);角角边(AAS); 斜边直角边(HL).
由边边边(SSS)可猜想:
三边对应成比例的两个三角形相似;
由边角边(SAS)可猜想:
两边对应成比例,且夹角相等的两个三角形相似;由角边角(ASA);角角边(AAS)可猜想:两个角对应相等的两个三角形相似;
由斜边直角边(HL)可猜想:
斜边直角边对应成比例的两个直角三角形相似.
如何把我们的猜想变为现实?(证明)问题一:
如果△ ABC与△ A′B′C′三边对应成比例,那么它们一定相似吗?我们一起来动手:
画△ ABC与△ A′B′C′,设法比较∠A与∠A′的大小, ∠B与∠B′的大小,∠C与∠C′的大小.
△ ABC与△ A′B′C′相似吗?说说你的理由.
改变k值的大小(如1∶3),再试一试.
通过上面的活动,你猜出了什么结论?判定三角形相似的方法之二三边对应成比例的两个三角形相似.如图,在△ ABC与△ A′B′C′中,如果那么△ ABC∽ △ A′B′C′
(三边对应成比例的两个三角形相似.)(SSS)下面两个三角形是否相似?为什么?解:在△ABC和△DEF中.∴△ ABC ∽ △ ADE.(三边对应边成比例的两个三角形相似.)三边对应成比例的两个三角形相似.如图,△ ABC与△ A′B′C′相似吗?
你用什么方法来支持你的判断?∴△ ABC∽△ A′B′C′
(三边对应成比例的两个三角形相似.)解:如图,设小正方形的边长为1,由勾股定理可得:问题二:
如果△ ABC与△ A′B′C′两边对应成比例,且这两边的夹角相等.那么它们一定相似吗?我们一起来动手:
画△ ABC与△ A′B′C′,设法比较它们的第三组对应边BC和B′C′的大小, 它们的比等于K吗?
△ ABC与△ A′B′C′相似吗?说说你的理由.
改变k值或∠A的大小再试一试.
通过上面的活动,你猜出了什么结论?判定三角形相似的方法之三两边对应成比例,并且相应的夹角相等,这两个三角形相似.如图,在△ ABC与△ A′B′C′中,如果那么△ ABC∽ △ A′B′C′
(两边对应成比例且夹角相等的两个三角形相似.)(SAS)例 如图矩形ABCD是由三个正方形ABEG,GEFH,HFCD组成的,找出图中的相似三角形.解:△ AEF∽ △CEA.理由是:
设小正方形的边长是1,由勾股定理得∴△ AEF ∽ △CEA.
(三边对应边成比例的两个三角形相似.)∴△ AEF ∽ △CEA.
(两条对应边成比例且它们的夹角对应相等的两个三角形相似.)∵∠ AEF = ∠CEA=135°. 上述判定方法中的“角”一定是两对应边的夹角吗?三 同步训练你掌握了吗?四 思维拓展★ 探讨了相似三角形的另两种判定方法:★ 数学活动充满着探索与创新,请同学们利用所学知识解决生活中的实际问题. 如图,△ABC与△ A’ B’ C’ 相似吗?你有哪些判断方法?试试你的能力 有一池塘, 周围都是空地. 如果要测量池塘两端A、B间的距离, 你能利用本节所学的知识解决这个问题吗???AB △ABC的顶点A、B、C在单位正方形的顶点上 ,请在图中画一个△A1B1C1 使
△ A1B1C1 ∽△ABC
(相似比不为1),
且点都在单位正方形
的顶点上 . 在正方形方格中,CAB五 课时小结判定三角形相似的常用方法:
三边对应成比例的两个三角形相似.
两边对应成比例并且夹角相等的两个三角形相似.
相似三角形的各对应角相等,各对应边对应成比例.那么△ ABC∽ △DEF.那么△ ABC∽ △结束寄语可以用一次的想法是一个决窍,如果它可以用两次以上,那就成为一种方法了.
