【全程同步】2013-2014学年高中数学必修一:23幂函数 教师用书配套课件(56张ppt)
文档属性
| 名称 | 【全程同步】2013-2014学年高中数学必修一:23幂函数 教师用书配套课件(56张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-02 00:00:00 | ||
图片预览










文档简介
课件56张PPT。2.3 幂函数 一、幂函数的定义
1.解析式:_____.
2.自变量:__,常数:___.
思考:一次函数与二次函数一定是幂函数吗?
提示:不一定.例如:一次函数y=x+1,二次函数y=x2+1等都
不是幂函数.y=xαxα二、幂函数的图象与性质
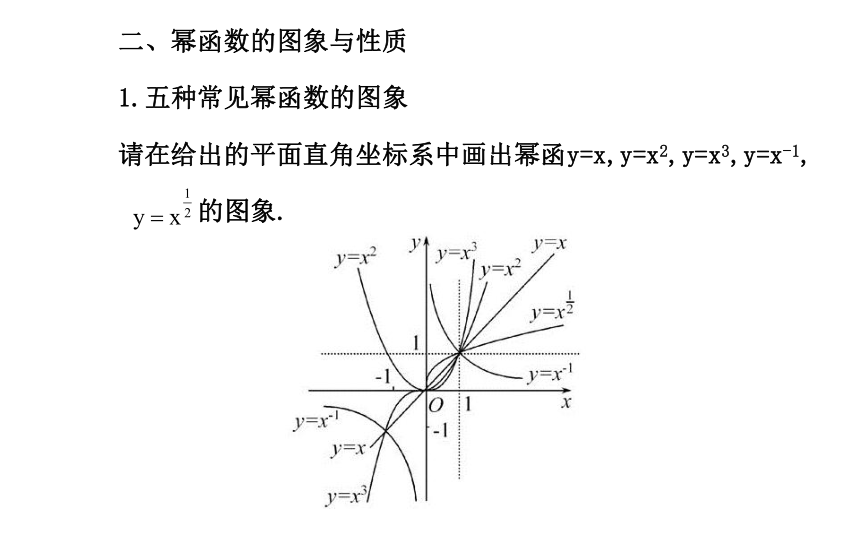
1.五种常见幂函数的图象
请在给出的平面直角坐标系中画出幂函y=x,y=x2,y=x3,y=x-1,
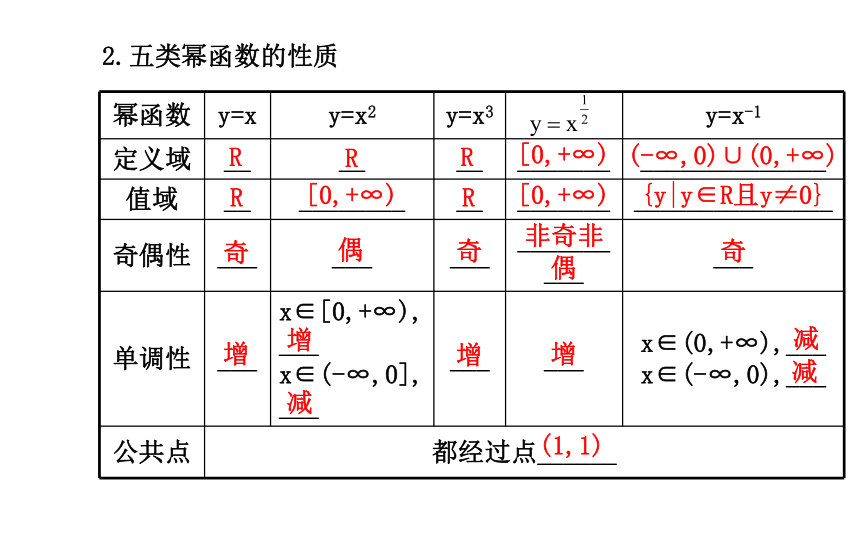
的图象.2.五类幂函数的性质RRR[0,+∞)(-∞,0)∪(0,+∞)R[0,+∞)R[0,+∞){y|y∈R且y≠0}奇偶奇非奇非偶奇增增减增增减减(1,1)判断:(正确的打“√”,错误的打“×”)
(1)幂函数的图象必过点(0,0)和(1,1).( )
(2)幂函数y=xα的定义域、奇偶性、单调性,因函数式中α的不同而各异.( )
(3)幂函数的图象可以出现在平面直角坐标系中的任意一个象限.( )提示:(1)错误.当α>0时,幂函数y=xα的图象必过点(0,0)和(1,1);当α<0时,幂函数y=xα的图象必过点(1,1),不过点(0,0).
(2)正确.由五类幂函数的性质可知此说法正确.
(3)错误.对幂函数y=xα而言,当x>0时,必有y>0,故幂函数的图象不过第四象限.
答案:(1)× (2)√ (3)×【知识点拨】
1.幂函数解析式的结构特征
(1)指数为常数.
(2)底数是自变量,自变量的系数为1.
(3)幂xα的系数为1.
(4)只有1项.2.幂函数与指数函数比较3.幂函数y=xα在第一象限的图象特征
(1)指数大于1,在第一象限为抛物线型(下凸).
(2)指数等于1,在第一象限为上升的射线(去掉端点).
(3)指数大于0小于1,在第一象限为抛物线型(上凸).
(4)指数等于0,在第一象限为水平的射线(去掉端点).
(5)指数小于0,在第一象限为双曲线型.4.幂函数的单调性
(1)如果α>0,幂函数y=xα在(0,+∞)上是增函数.
(2)如果α<0,幂函数y=xα在(0,+∞)上是减函数.类型 一 幂函数的概念
【典型例题】
1.给出下列函数:
①y= ②y=3x-2;③y=x4+x2;④
⑤y=(x-1)2;⑥y=0.3x,其中是幂函数的有( )
A.1个 B.2个 C.3个 D.4个
2.已知函数 当m为何值时,f(x)是
幂函数?【解题探究】1.判断一个函数是否是幂函数的依据是什么?
2.根据幂函数定义可知,题2中的字母应满足哪些条件?探究提示:
1.判断一个函数是否是幂函数的依据是幂函数的解析式具有的四个特征:
(1)指数为常数.
(2)底数是自变量,自变量的系数为1.
(3)幂xα的系数为1.
(4)只有1项.
2.m应满足m2+2m-2=1.【解析】1.选B.可以对照幂函数的定义进行判断.在所给出
的六个函数中,只有y= =x-3和 符合幂函数的定
义,是幂函数,其余四个都不是幂函数.
2.要使 是幂函数,则有m2+2m-2=1,即
m2+2m-3=0,解得m=-3或m=1.【拓展提升】
1.幂函数的判断方法
(1)幂函数同指数函数、对数函数一样,是一种“形式定义”的函数,也就是说必须完全具备形如y=xα(α∈R)的函数才是幂函数.
(2)如果函数解析式以根式的形式给出,则要注意把根式化为分数指数幂的形式进行化简整理,再对照幂函数的定义进行判断.2.求幂函数解析式的依据及常用方法
(1)依据.
若一个函数为幂函数,则该函数应具备幂函数解析式所具备的特征,这是解决与幂函数有关问题的隐含条件.
(2)常用方法.
设幂函数解析式为f(x)=xα,根据条件求出α.【变式训练】已知点( )在幂函数f(x)的图象上,则f(x)
的表达式为( )
A.f(x)=x3 B.f(x)=x-3
C.f(x)= D.f(x)=
【解析】选B.设f(x)=xα,则
即 ∴α=-3,∴f(x)=x-3.类型 二 幂函数的图象
【典型例题】
1.(2013·三明高一检测)函数y= 的图象大致是( )2.(2013·邢台高一检测)当α∈{-1, 1,3}时,幂函数
y=xα的图象不可能经过第______象限.
3.已知幂函数y=xm-2(m∈N)的图象与x,y轴都无交点,且关于
y轴对称,求m的值,并画出它的图象.【解题探究】1.可以根据函数的哪些性质判断函数的图象的
特征?
2.幂函数y=x-1,y= y=x,y=x3的图象分布在哪些象限?
3.题3中幂函数的图象与x,y轴都无交点,且关于y轴对称,揭
示了幂指数m-2是什么数?探究提示:
1.可以根据函数的奇偶性、图象上的特殊点和线判断函数的
图象的特征.
2.幂函数y=x-1,y=x,y=x3的图象分布在第一、三象限,
y= 的图象分布在第一象限.
3.图象与x,y轴都无交点,揭示了幂指数m-2是负数或零;关
于y轴对称且m∈N揭示了幂指数m-2是偶数.【解析】1.选B.函数 是定义域为R的奇函数,且此
函数在定义域上是增函数,其图象关于原点对称,排除A,C.
另外,因为
所以当x∈(0,1)时,函数y= 的图象在直线y=x的下方;
当x∈(1,+∞)时,函数y= 的图象在直线y=x的上方.故选B.2.幂函数y=x-1,y=x,y=x3的图象分布在第一、三象限,
y= 的图象分布在第一象限.
所以幂函数y=xα(α=-1, 1,3)的图象不可能经过第二、
四象限.
答案:二、四3.∵图象与x,y轴都无交点,
∴m-2≤0,即m≤2.
又m∈N,∴m=0,1,2.
∵幂函数图象关于y轴对称,
∴m=0,或m=2.
当m=0时,函数为y=x-2,图象如图1;
当m=2时,函数为y=x0=1(x≠0),
图象如图2.【互动探究】题1中,若将函数y= 改为y= 其图象大
致是所给四个选项中的哪个图象?
【解析】函数 是定义域为{x|x≠0}的奇函数,
其图象关于原点对称.
由此知函数y= 的图象大致是选项A的图象.【拓展提升】
1.作幂函数图象的原则和方法
(1)原则:作幂函数的图象要联系函数的定义域、值域、单调性、奇偶性等.
(2)方法:首先作出幂函数在第一象限内的图象,然后根据奇偶性就可作出幂函数在定义域内完整的图象.2.幂函数y=xα在第一象限内图象的画法
(1)当α<0时,其图象可以类似y=x-1画出;
(2)当0<α<1时,其图象可以类似y= 画出;
(3)当α>1时,其图象可以类似y=x2画出.【变式训练】函数f(x)=xn+ax-1(n∈Z,a>0且a≠1)的图象必过定点( )
A.(1,1) B.(1,2)
C.(-1,0) D.(-1,1)
【解析】选B.因为f(1)=1n+a1-1=1+1=2,所以f(x)=xn+ax-1
(n∈Z,a>0且a≠1)的图象必过定点(1,2).类型 三 幂函数的性质及应用
【典型例题】
1.设α∈{ },则使函数y=xα的定义域为R的所有α
的值为( )
A.1,3 B.-1,1
C.-1,3 D.-1,1,3
2.判断下列各组数的大小
(1)5.1-2与5.09-2的大小关系是______.
(2) 的大小关系是______.3.(2013·长沙高一检测)已知函数f(x)= +1.
(1)判断函数f(x)在区间(0,+∞)上的单调性并证明.
(2)求f(x)在区间[1,3]上的最大值和最小值.【解题探究】1.幂函数y=xα的定义域与α有什么关系?
2.(1)要比较题2(1)中两个数的大小,可将其看作哪个函数的函数值?如何利用函数的单调性比较大小?
(2)三个(三个以上的)数比较大小,要注意应用什么方法?
3.利用定义法判断函数的单调性的步骤是什么?探究提示:
1.当α为正整数时,幂函数y=xα的定义域为R.当α为负数或分数时,要先用负整数幂、分数指数幂的意义变形后再求定义域.
2.(1)5.1-2和5.09-2可以看作函数y=x-2在自变量分别取5.1和5.09时的函数值.根据函数y=x-2的单调性,可以由5.1和5.09的大小关系推出5.1-2和5.09-2的大小关系.
(2)三个(三个以上的)数比较大小,要注意应用中间量法.
3.按照设元、作差、变形、判号、下结论五个步骤进行.【解析】1.选A.函数y=x,y=x3的定义域是R. 的
定义域是(0,+∞).
y= 的定义域是[0,+∞).
y=x-1的定义域是{x|x≠0}.2.(1)∵y=x-2在(0,+∞)上为减函数,
且5.1>5.09,
∴5.1-2<5.09-2.
(2)
∵y= 在(0,+∞)上为增函数,且
∴ 又
∴
答案:(1)5.1-2<5.09-2
(2)3.(1)函数f(x)在区间(0,+∞)上是减函数.
证明如下:
设x1,x2是区间(0,+∞)上任意两个实数,且x1<x2,则
∵x2>x1>0,
∴x1+x2>0,x2-x1>0,(x1x2)2>0,
∴f(x1)-f(x2)>0,即f(x1)>f(x2),
所以函数f(x)在区间(0,+∞)上是减函数.(2)由(1)知函数f(x)在区间[1,3]上是减函数,
所以当x=1时,取最大值,最大值为f(1)=2,
当x=3时,取最小值,最小值为f(3)=【拓展提升】
1.求幂函数y=xα(其中α是分数形式)定义域的基本步骤
(1)把分数指数幂化为根式的形式.
(2)根据根式和分式有意义的条件列不等式(组)求解.2.利用幂函数单调性比较大小的三种基本方法
3.利用幂函数单调性比较大小时要注意的问题
比较大小的两个实数必须在同一函数的同一单调区间内,否则无法比较大小.【变式训练】已知函数f(x)=xm- 且f(4)=
(1)求m的值.
(2)判定f(x)的奇偶性.
(3)判断f(x)在(0,+∞)上的单调性,并给予证明.【解析】(1)因为f(4)= 所以
所以m=1.
(2)由(1)知f(x)=
因为f(x)的定义域为{x|x≠0},
又
所以f(x)是奇函数.(3)f(x)在(0,+∞)上单调递增.
设x1>x2>0,则
因为x1>x2>0,
所以x1-x2>0,
所以f(x1)>f(x2),
所以f(x)在(0,+∞)上为单调递增函数.【易错误区】解答幂函数性质问题的误区
【典例】(2013·遵义高一检测)幂函数f(x)=x3m-5(m∈N)在(0,+∞)上是减函数,且f(-x)=f(x),则m可能等于( )
A.0 B.1 C.2 D.0或1【解析】选B.因为f(x)=x3m-5(m∈N)在(0,+∞)上是减函数,
所以3m-5<0,故m< 又因为m∈N,所以m=0或m=1.
当m=0时,f(x)=x-5,f(-x)≠f(x)①,不符合题意;
当m=1时,f(x)=x-2,
f(-x)=f(x),符合题意.
综上知,m=1.【类题试解】已知幂函数 在区间(0,+∞)上
是增函数,则实数m的值为( )
A.3 B.2 C.2或3 D.-2或-3
【解析】选A.因为函数 是幂函数,
所以m2-5m+7=1,即m2-5m+6=0,解得m=2或m=3.
当m=2时,f(x)=x-2在(0,+∞)上是减函数,不符合题意;
当m=3时,f(x)=x3在(0,+∞)上是增函数,符合题意.
所以m=3.【误区警示】【防范措施】
1.重视幂函数单调性的分析
幂函数在(0,+∞)上的单调性与幂函数指数的正负有密切的关系.例如本例中的幂函数在(0,+∞)上是减函数,所以可以分析出指数3m-5<0.
2.注意解题的入手点
解题要注意选准解题的入手点,否则容易陷入误区.例如,解答本例要首先由单调性和m∈N入手,求出m所有可能的取值,然后根据f(-x)=f(x)进行检验,并确定答案.1.下列给出的函数中,幂函数是( )
A.y=3x B.y=2x3 C.y= D.y=x3-1
【解析】选C.根据幂函数的定义可知 是幂函数.2.下列幂函数中图象过点(0,0),(1,1),且是偶函数的是( )
A.y= B.y=x4 C.y=x-2 D.y=
【解析】选B.函数y= y= 不是偶函数,函数y=x-2是偶
函数,其图象不过点(0,0).函数y=x4的图象过点(0,0),(1,1)
且是偶函数.3.已知f(x)= 若0<a<b<1,则下列各式中正确的是( )
A.
B.
C.
D.【解析】选C.因为0<a<b<1,
所以0<a<b<1< <
因为f(x)= 在(0,+∞)上为增函数,
所以4.已知二次函数f(x)是幂函数,则f(x)的解析式为______.
【解析】由题意得f(x)=x2.
答案:f(x)=x25.若幂函数y=f(x)的图象经过点(9, ),则f(25)的值是______.
【解析】设f(x)=xα,则 =9α,3-1=32α,
解得α= 所以f(x)=
答案:6.求下列幂函数的定义域,并指出其奇偶性.
(1)y=x-2. (2)y=
【解析】(1) 定义域是{x|x≠0},是偶函数.
(2) 定义域是R,是偶函数.
1.解析式:_____.
2.自变量:__,常数:___.
思考:一次函数与二次函数一定是幂函数吗?
提示:不一定.例如:一次函数y=x+1,二次函数y=x2+1等都
不是幂函数.y=xαxα二、幂函数的图象与性质
1.五种常见幂函数的图象
请在给出的平面直角坐标系中画出幂函y=x,y=x2,y=x3,y=x-1,
的图象.2.五类幂函数的性质RRR[0,+∞)(-∞,0)∪(0,+∞)R[0,+∞)R[0,+∞){y|y∈R且y≠0}奇偶奇非奇非偶奇增增减增增减减(1,1)判断:(正确的打“√”,错误的打“×”)
(1)幂函数的图象必过点(0,0)和(1,1).( )
(2)幂函数y=xα的定义域、奇偶性、单调性,因函数式中α的不同而各异.( )
(3)幂函数的图象可以出现在平面直角坐标系中的任意一个象限.( )提示:(1)错误.当α>0时,幂函数y=xα的图象必过点(0,0)和(1,1);当α<0时,幂函数y=xα的图象必过点(1,1),不过点(0,0).
(2)正确.由五类幂函数的性质可知此说法正确.
(3)错误.对幂函数y=xα而言,当x>0时,必有y>0,故幂函数的图象不过第四象限.
答案:(1)× (2)√ (3)×【知识点拨】
1.幂函数解析式的结构特征
(1)指数为常数.
(2)底数是自变量,自变量的系数为1.
(3)幂xα的系数为1.
(4)只有1项.2.幂函数与指数函数比较3.幂函数y=xα在第一象限的图象特征
(1)指数大于1,在第一象限为抛物线型(下凸).
(2)指数等于1,在第一象限为上升的射线(去掉端点).
(3)指数大于0小于1,在第一象限为抛物线型(上凸).
(4)指数等于0,在第一象限为水平的射线(去掉端点).
(5)指数小于0,在第一象限为双曲线型.4.幂函数的单调性
(1)如果α>0,幂函数y=xα在(0,+∞)上是增函数.
(2)如果α<0,幂函数y=xα在(0,+∞)上是减函数.类型 一 幂函数的概念
【典型例题】
1.给出下列函数:
①y= ②y=3x-2;③y=x4+x2;④
⑤y=(x-1)2;⑥y=0.3x,其中是幂函数的有( )
A.1个 B.2个 C.3个 D.4个
2.已知函数 当m为何值时,f(x)是
幂函数?【解题探究】1.判断一个函数是否是幂函数的依据是什么?
2.根据幂函数定义可知,题2中的字母应满足哪些条件?探究提示:
1.判断一个函数是否是幂函数的依据是幂函数的解析式具有的四个特征:
(1)指数为常数.
(2)底数是自变量,自变量的系数为1.
(3)幂xα的系数为1.
(4)只有1项.
2.m应满足m2+2m-2=1.【解析】1.选B.可以对照幂函数的定义进行判断.在所给出
的六个函数中,只有y= =x-3和 符合幂函数的定
义,是幂函数,其余四个都不是幂函数.
2.要使 是幂函数,则有m2+2m-2=1,即
m2+2m-3=0,解得m=-3或m=1.【拓展提升】
1.幂函数的判断方法
(1)幂函数同指数函数、对数函数一样,是一种“形式定义”的函数,也就是说必须完全具备形如y=xα(α∈R)的函数才是幂函数.
(2)如果函数解析式以根式的形式给出,则要注意把根式化为分数指数幂的形式进行化简整理,再对照幂函数的定义进行判断.2.求幂函数解析式的依据及常用方法
(1)依据.
若一个函数为幂函数,则该函数应具备幂函数解析式所具备的特征,这是解决与幂函数有关问题的隐含条件.
(2)常用方法.
设幂函数解析式为f(x)=xα,根据条件求出α.【变式训练】已知点( )在幂函数f(x)的图象上,则f(x)
的表达式为( )
A.f(x)=x3 B.f(x)=x-3
C.f(x)= D.f(x)=
【解析】选B.设f(x)=xα,则
即 ∴α=-3,∴f(x)=x-3.类型 二 幂函数的图象
【典型例题】
1.(2013·三明高一检测)函数y= 的图象大致是( )2.(2013·邢台高一检测)当α∈{-1, 1,3}时,幂函数
y=xα的图象不可能经过第______象限.
3.已知幂函数y=xm-2(m∈N)的图象与x,y轴都无交点,且关于
y轴对称,求m的值,并画出它的图象.【解题探究】1.可以根据函数的哪些性质判断函数的图象的
特征?
2.幂函数y=x-1,y= y=x,y=x3的图象分布在哪些象限?
3.题3中幂函数的图象与x,y轴都无交点,且关于y轴对称,揭
示了幂指数m-2是什么数?探究提示:
1.可以根据函数的奇偶性、图象上的特殊点和线判断函数的
图象的特征.
2.幂函数y=x-1,y=x,y=x3的图象分布在第一、三象限,
y= 的图象分布在第一象限.
3.图象与x,y轴都无交点,揭示了幂指数m-2是负数或零;关
于y轴对称且m∈N揭示了幂指数m-2是偶数.【解析】1.选B.函数 是定义域为R的奇函数,且此
函数在定义域上是增函数,其图象关于原点对称,排除A,C.
另外,因为
所以当x∈(0,1)时,函数y= 的图象在直线y=x的下方;
当x∈(1,+∞)时,函数y= 的图象在直线y=x的上方.故选B.2.幂函数y=x-1,y=x,y=x3的图象分布在第一、三象限,
y= 的图象分布在第一象限.
所以幂函数y=xα(α=-1, 1,3)的图象不可能经过第二、
四象限.
答案:二、四3.∵图象与x,y轴都无交点,
∴m-2≤0,即m≤2.
又m∈N,∴m=0,1,2.
∵幂函数图象关于y轴对称,
∴m=0,或m=2.
当m=0时,函数为y=x-2,图象如图1;
当m=2时,函数为y=x0=1(x≠0),
图象如图2.【互动探究】题1中,若将函数y= 改为y= 其图象大
致是所给四个选项中的哪个图象?
【解析】函数 是定义域为{x|x≠0}的奇函数,
其图象关于原点对称.
由此知函数y= 的图象大致是选项A的图象.【拓展提升】
1.作幂函数图象的原则和方法
(1)原则:作幂函数的图象要联系函数的定义域、值域、单调性、奇偶性等.
(2)方法:首先作出幂函数在第一象限内的图象,然后根据奇偶性就可作出幂函数在定义域内完整的图象.2.幂函数y=xα在第一象限内图象的画法
(1)当α<0时,其图象可以类似y=x-1画出;
(2)当0<α<1时,其图象可以类似y= 画出;
(3)当α>1时,其图象可以类似y=x2画出.【变式训练】函数f(x)=xn+ax-1(n∈Z,a>0且a≠1)的图象必过定点( )
A.(1,1) B.(1,2)
C.(-1,0) D.(-1,1)
【解析】选B.因为f(1)=1n+a1-1=1+1=2,所以f(x)=xn+ax-1
(n∈Z,a>0且a≠1)的图象必过定点(1,2).类型 三 幂函数的性质及应用
【典型例题】
1.设α∈{ },则使函数y=xα的定义域为R的所有α
的值为( )
A.1,3 B.-1,1
C.-1,3 D.-1,1,3
2.判断下列各组数的大小
(1)5.1-2与5.09-2的大小关系是______.
(2) 的大小关系是______.3.(2013·长沙高一检测)已知函数f(x)= +1.
(1)判断函数f(x)在区间(0,+∞)上的单调性并证明.
(2)求f(x)在区间[1,3]上的最大值和最小值.【解题探究】1.幂函数y=xα的定义域与α有什么关系?
2.(1)要比较题2(1)中两个数的大小,可将其看作哪个函数的函数值?如何利用函数的单调性比较大小?
(2)三个(三个以上的)数比较大小,要注意应用什么方法?
3.利用定义法判断函数的单调性的步骤是什么?探究提示:
1.当α为正整数时,幂函数y=xα的定义域为R.当α为负数或分数时,要先用负整数幂、分数指数幂的意义变形后再求定义域.
2.(1)5.1-2和5.09-2可以看作函数y=x-2在自变量分别取5.1和5.09时的函数值.根据函数y=x-2的单调性,可以由5.1和5.09的大小关系推出5.1-2和5.09-2的大小关系.
(2)三个(三个以上的)数比较大小,要注意应用中间量法.
3.按照设元、作差、变形、判号、下结论五个步骤进行.【解析】1.选A.函数y=x,y=x3的定义域是R. 的
定义域是(0,+∞).
y= 的定义域是[0,+∞).
y=x-1的定义域是{x|x≠0}.2.(1)∵y=x-2在(0,+∞)上为减函数,
且5.1>5.09,
∴5.1-2<5.09-2.
(2)
∵y= 在(0,+∞)上为增函数,且
∴ 又
∴
答案:(1)5.1-2<5.09-2
(2)3.(1)函数f(x)在区间(0,+∞)上是减函数.
证明如下:
设x1,x2是区间(0,+∞)上任意两个实数,且x1<x2,则
∵x2>x1>0,
∴x1+x2>0,x2-x1>0,(x1x2)2>0,
∴f(x1)-f(x2)>0,即f(x1)>f(x2),
所以函数f(x)在区间(0,+∞)上是减函数.(2)由(1)知函数f(x)在区间[1,3]上是减函数,
所以当x=1时,取最大值,最大值为f(1)=2,
当x=3时,取最小值,最小值为f(3)=【拓展提升】
1.求幂函数y=xα(其中α是分数形式)定义域的基本步骤
(1)把分数指数幂化为根式的形式.
(2)根据根式和分式有意义的条件列不等式(组)求解.2.利用幂函数单调性比较大小的三种基本方法
3.利用幂函数单调性比较大小时要注意的问题
比较大小的两个实数必须在同一函数的同一单调区间内,否则无法比较大小.【变式训练】已知函数f(x)=xm- 且f(4)=
(1)求m的值.
(2)判定f(x)的奇偶性.
(3)判断f(x)在(0,+∞)上的单调性,并给予证明.【解析】(1)因为f(4)= 所以
所以m=1.
(2)由(1)知f(x)=
因为f(x)的定义域为{x|x≠0},
又
所以f(x)是奇函数.(3)f(x)在(0,+∞)上单调递增.
设x1>x2>0,则
因为x1>x2>0,
所以x1-x2>0,
所以f(x1)>f(x2),
所以f(x)在(0,+∞)上为单调递增函数.【易错误区】解答幂函数性质问题的误区
【典例】(2013·遵义高一检测)幂函数f(x)=x3m-5(m∈N)在(0,+∞)上是减函数,且f(-x)=f(x),则m可能等于( )
A.0 B.1 C.2 D.0或1【解析】选B.因为f(x)=x3m-5(m∈N)在(0,+∞)上是减函数,
所以3m-5<0,故m< 又因为m∈N,所以m=0或m=1.
当m=0时,f(x)=x-5,f(-x)≠f(x)①,不符合题意;
当m=1时,f(x)=x-2,
f(-x)=f(x),符合题意.
综上知,m=1.【类题试解】已知幂函数 在区间(0,+∞)上
是增函数,则实数m的值为( )
A.3 B.2 C.2或3 D.-2或-3
【解析】选A.因为函数 是幂函数,
所以m2-5m+7=1,即m2-5m+6=0,解得m=2或m=3.
当m=2时,f(x)=x-2在(0,+∞)上是减函数,不符合题意;
当m=3时,f(x)=x3在(0,+∞)上是增函数,符合题意.
所以m=3.【误区警示】【防范措施】
1.重视幂函数单调性的分析
幂函数在(0,+∞)上的单调性与幂函数指数的正负有密切的关系.例如本例中的幂函数在(0,+∞)上是减函数,所以可以分析出指数3m-5<0.
2.注意解题的入手点
解题要注意选准解题的入手点,否则容易陷入误区.例如,解答本例要首先由单调性和m∈N入手,求出m所有可能的取值,然后根据f(-x)=f(x)进行检验,并确定答案.1.下列给出的函数中,幂函数是( )
A.y=3x B.y=2x3 C.y= D.y=x3-1
【解析】选C.根据幂函数的定义可知 是幂函数.2.下列幂函数中图象过点(0,0),(1,1),且是偶函数的是( )
A.y= B.y=x4 C.y=x-2 D.y=
【解析】选B.函数y= y= 不是偶函数,函数y=x-2是偶
函数,其图象不过点(0,0).函数y=x4的图象过点(0,0),(1,1)
且是偶函数.3.已知f(x)= 若0<a<b<1,则下列各式中正确的是( )
A.
B.
C.
D.【解析】选C.因为0<a<b<1,
所以0<a<b<1< <
因为f(x)= 在(0,+∞)上为增函数,
所以4.已知二次函数f(x)是幂函数,则f(x)的解析式为______.
【解析】由题意得f(x)=x2.
答案:f(x)=x25.若幂函数y=f(x)的图象经过点(9, ),则f(25)的值是______.
【解析】设f(x)=xα,则 =9α,3-1=32α,
解得α= 所以f(x)=
答案:6.求下列幂函数的定义域,并指出其奇偶性.
(1)y=x-2. (2)y=
【解析】(1) 定义域是{x|x≠0},是偶函数.
(2) 定义域是R,是偶函数.
