27.2.1 相似三角形的判定(3)[下学期]
文档属性
| 名称 | 27.2.1 相似三角形的判定(3)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 590.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-25 00:00:00 | ||
图片预览





文档简介
课件26张PPT。 玉环实验学校 27.2.1相似三角形的判定(3)一 温故知新判定三角形相似的方法判定两个三角形相似的方法之一:
平行于三角形一边的直线和其他两边相交(或两边的延长线相交 ) 所构成的三角形与原三角形相似.
判定两个三角形相似的方法之二:
三边对应成比例的两个三角形相似.
判定两个三角形相似的方法之三:
两边对应成比例,并且相应的夹角相等,这两个三角形相似.
你能否得出判定三角形相似的其它方法?二 探究新知探究3 作△ABC和△DEF,使得∠A=∠D,∠B=∠E,这时它们的第三个角满足∠C=∠F吗?分别度量这两个三角形的边长,计算
,你有什么发现?
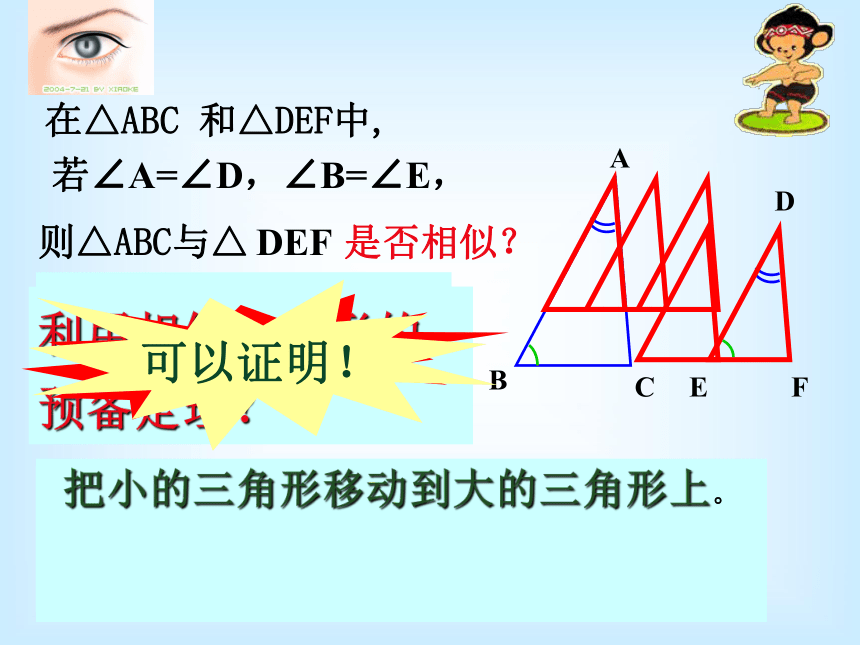
把你的结果与邻座的同学比较,你们的结论一样吗?△ABC和△DEF相似吗?怎样创造具备预备定理条件的图形?在△ABC 和△DEF中,则△ABC与△ DEF是否相似?利用相似三角形的定义?利用相似三角形的预备定理? 条件不够可以证明!若∠A=∠D,∠B=∠E,把小的三角形移动到大的三角形上。
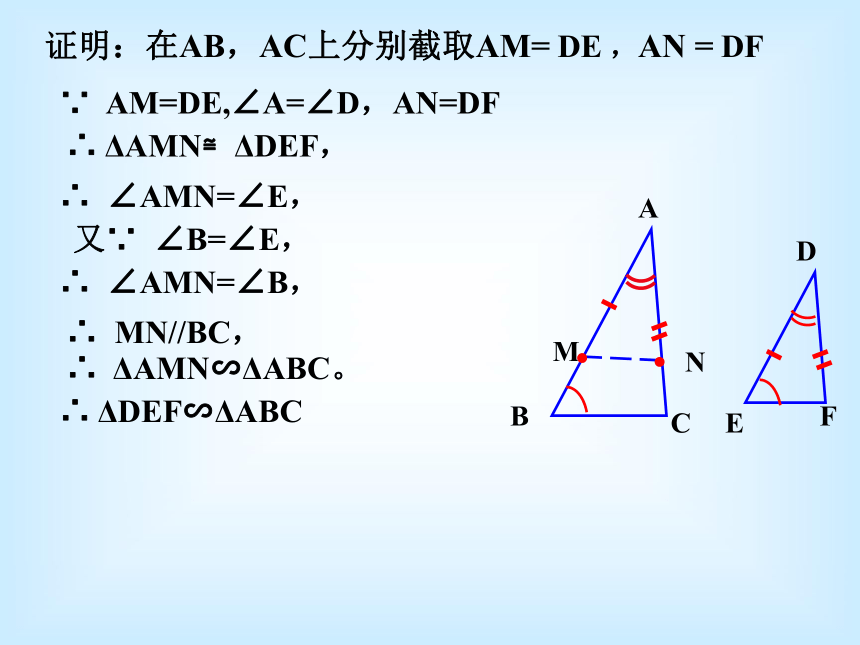
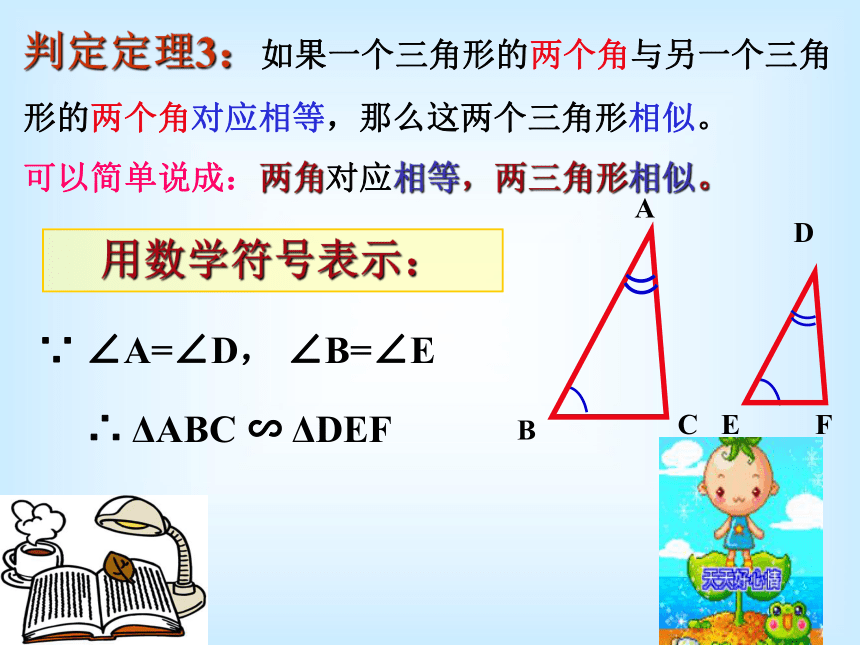
ABCD F E ∵ AM=DE,∠A=∠D,AN=DF∴ ΔAMN≌ΔDEF,∴ ∠AMN=∠E,又∵ ∠B=∠E,∴ ∠AMN=∠B,∴ MN//BC,∴ ΔAMN∽ΔABC。∴ ΔDEF∽ΔABC证明:在AB,AC上分别截取AM= DE ,AN = DFCF∵ ∠A=∠D, ∠B=∠E∴ ΔABC ∽ ΔDEF用数学符号表示:判定定理3:如果一个三角形的两个角与另一个三角
形的两个角对应相等,那么这两个三角形相似。
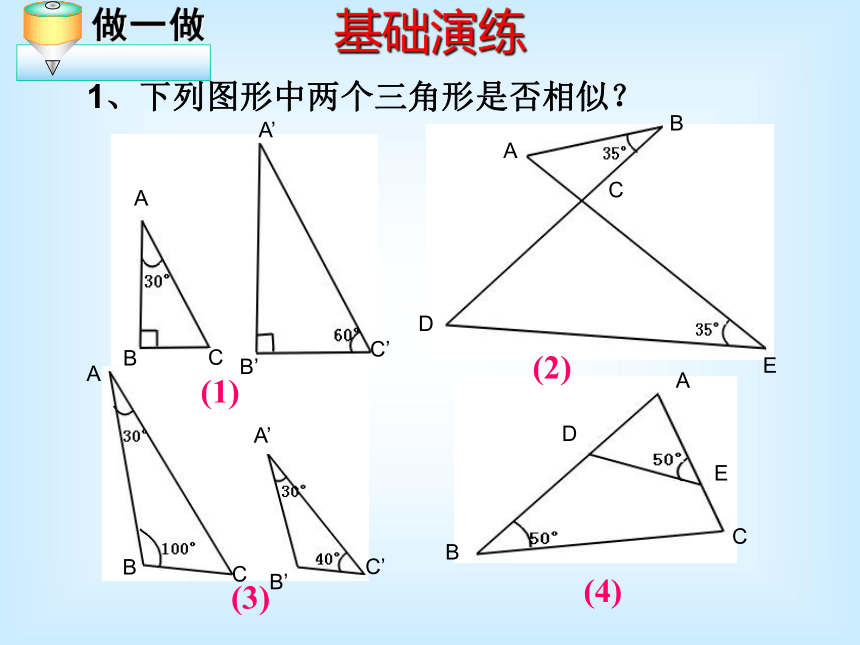
可以简单说成:两角对应相等,两三角形相似。基础演练1、下列图形中两个三角形是否相似?(1)(2)(3)(4)2、判断题:
⑴所有的直角三角形都相似 . ( )
⑵有一个锐角对应相等的两直角三角形相似.( )
⑶所有的等边三角形都相似. ( )
⑷所有的等腰直角三角形都相似. ( )
⑸顶角相等的两个等腰三角形相似. ( )
⑹有一个角相等的两个等腰三角形相似. ( )
×√√ √√×如图,弦AB和CD相交于OO内一点P,
求证:PA ? PB = PC?PD?例题讲解三 同步训练例3:如图,CD交BE于点A,AD·AC=AE·BA,求证:∠E=∠C大展身手(变式):如图,CD交BE于点A, ∠E=∠C,
求证: AD·AC=AE·BA1、已知如图直线BE、DC交于A , ∠E= ∠C
求证:DA·AC=AB·AEDEABC12证明:
∵ ∠E=∠C ∠1=∠2
∴ △ABC ∽ △ADE
∴ AC :AE=AB :AD
∴ DA · AC=AB · AEEABDC解: ∵ ∠ A= ∠ A ∠ABD=∠C
∴ △ABD ∽ △ACB
∴ AB : AC=AD : AB
∴ AB2 = AD · AC
∵ AD=2 AC=8
∴ AB =4已知如图, ∠ABD=∠C AD=2 AC=8,求AB ABDC3、如图:在Rt △ ABC中, ∠ABC=900,BD⊥AC于D
问:①图中有几个直角三角形?它们相似吗?为什么?解: 图中有三个直角三角形,分别是: △ ABC、
△ ADB、 △ BDC
△ ABC ∽ △ ADB ∽ △ BDC
例题解析: 直角三角形被斜边上的高分成的两个直角三角形和原三角形相似.已知:如图, Rt△ABC中,CD是斜边的高.求证:△ABC ∽ △CBD ∽ △ACD DBC3、如图:在Rt △ ABC中 , ∠ABC=90° BD⊥AC于D
② 求证:AB2=AD · AC BD2=AD · DCA 证明 ∵ ∠ABC=900,BD⊥AC
∴ △ ADB ∽ △ ABC
∴AB∶AC=AD∶AB
∴AB2=AD · AC
∵ ∠ABC=900,BD⊥AC
∴ △ ADB ∽ △ CDB
∴ AD∶BD=BD∶DC
∴ BD2=AD · DC
DBCA18 四 思维拓展E变式一:如图,G是□ ABCD的CD延长线上的一点,连结BG交对角线AC于E,交AD于F,则: (1)图中与△AEF相似的三角形有 .(2)图中与△ABC相似的三角形有 .(3)图中与△GFD相似的三角形有 . △CEB △CDA 、△BFA解后反思:运用定理判定两三角形相似,如何找准两对相等的角△GBC 变式二:如图,直线a、直线b相交于点A,点B、C分别在直线a、直线b上,在直线a、直线b上分别找两点D、E,使?BAC与?DAE相似,请尽量多地画出点D、E的位置.五 课时小结www.czsx.com.cn总结:
1、化归思想,将未知问题转化为已知问题
2、相似三角形的判定一:有两个角相等的两个三角形相似
3、直角三角形被斜边上的高分成的两个直角三角形和原三角形 相似
∵ ∠BAC= 900,BD⊥AC
∴ △ABC ∽ △DBA ∽ △DAC
4、证明线段的乘积问题可转化为线段的比例问题
ABDC3、如图:在Rt △ ABC中, ∠ABC=900,BD⊥AC于D ABDCEF问:若E是BC中点,ED的延长线交BA的延长线于F,
求证:AB : BC=DF : BF
平行于三角形一边的直线和其他两边相交(或两边的延长线相交 ) 所构成的三角形与原三角形相似.
判定两个三角形相似的方法之二:
三边对应成比例的两个三角形相似.
判定两个三角形相似的方法之三:
两边对应成比例,并且相应的夹角相等,这两个三角形相似.
你能否得出判定三角形相似的其它方法?二 探究新知探究3 作△ABC和△DEF,使得∠A=∠D,∠B=∠E,这时它们的第三个角满足∠C=∠F吗?分别度量这两个三角形的边长,计算
,你有什么发现?
把你的结果与邻座的同学比较,你们的结论一样吗?△ABC和△DEF相似吗?怎样创造具备预备定理条件的图形?在△ABC 和△DEF中,则△ABC与△ DEF是否相似?利用相似三角形的定义?利用相似三角形的预备定理? 条件不够可以证明!若∠A=∠D,∠B=∠E,把小的三角形移动到大的三角形上。
ABCD F E ∵ AM=DE,∠A=∠D,AN=DF∴ ΔAMN≌ΔDEF,∴ ∠AMN=∠E,又∵ ∠B=∠E,∴ ∠AMN=∠B,∴ MN//BC,∴ ΔAMN∽ΔABC。∴ ΔDEF∽ΔABC证明:在AB,AC上分别截取AM= DE ,AN = DFCF∵ ∠A=∠D, ∠B=∠E∴ ΔABC ∽ ΔDEF用数学符号表示:判定定理3:如果一个三角形的两个角与另一个三角
形的两个角对应相等,那么这两个三角形相似。
可以简单说成:两角对应相等,两三角形相似。基础演练1、下列图形中两个三角形是否相似?(1)(2)(3)(4)2、判断题:
⑴所有的直角三角形都相似 . ( )
⑵有一个锐角对应相等的两直角三角形相似.( )
⑶所有的等边三角形都相似. ( )
⑷所有的等腰直角三角形都相似. ( )
⑸顶角相等的两个等腰三角形相似. ( )
⑹有一个角相等的两个等腰三角形相似. ( )
×√√ √√×如图,弦AB和CD相交于OO内一点P,
求证:PA ? PB = PC?PD?例题讲解三 同步训练例3:如图,CD交BE于点A,AD·AC=AE·BA,求证:∠E=∠C大展身手(变式):如图,CD交BE于点A, ∠E=∠C,
求证: AD·AC=AE·BA1、已知如图直线BE、DC交于A , ∠E= ∠C
求证:DA·AC=AB·AEDEABC12证明:
∵ ∠E=∠C ∠1=∠2
∴ △ABC ∽ △ADE
∴ AC :AE=AB :AD
∴ DA · AC=AB · AEEABDC解: ∵ ∠ A= ∠ A ∠ABD=∠C
∴ △ABD ∽ △ACB
∴ AB : AC=AD : AB
∴ AB2 = AD · AC
∵ AD=2 AC=8
∴ AB =4已知如图, ∠ABD=∠C AD=2 AC=8,求AB ABDC3、如图:在Rt △ ABC中, ∠ABC=900,BD⊥AC于D
问:①图中有几个直角三角形?它们相似吗?为什么?解: 图中有三个直角三角形,分别是: △ ABC、
△ ADB、 △ BDC
△ ABC ∽ △ ADB ∽ △ BDC
例题解析: 直角三角形被斜边上的高分成的两个直角三角形和原三角形相似.已知:如图, Rt△ABC中,CD是斜边的高.求证:△ABC ∽ △CBD ∽ △ACD DBC3、如图:在Rt △ ABC中 , ∠ABC=90° BD⊥AC于D
② 求证:AB2=AD · AC BD2=AD · DCA 证明 ∵ ∠ABC=900,BD⊥AC
∴ △ ADB ∽ △ ABC
∴AB∶AC=AD∶AB
∴AB2=AD · AC
∵ ∠ABC=900,BD⊥AC
∴ △ ADB ∽ △ CDB
∴ AD∶BD=BD∶DC
∴ BD2=AD · DC
DBCA18 四 思维拓展E变式一:如图,G是□ ABCD的CD延长线上的一点,连结BG交对角线AC于E,交AD于F,则: (1)图中与△AEF相似的三角形有 .(2)图中与△ABC相似的三角形有 .(3)图中与△GFD相似的三角形有 . △CEB △CDA 、△BFA解后反思:运用定理判定两三角形相似,如何找准两对相等的角△GBC 变式二:如图,直线a、直线b相交于点A,点B、C分别在直线a、直线b上,在直线a、直线b上分别找两点D、E,使?BAC与?DAE相似,请尽量多地画出点D、E的位置.五 课时小结www.czsx.com.cn总结:
1、化归思想,将未知问题转化为已知问题
2、相似三角形的判定一:有两个角相等的两个三角形相似
3、直角三角形被斜边上的高分成的两个直角三角形和原三角形 相似
∵ ∠BAC= 900,BD⊥AC
∴ △ABC ∽ △DBA ∽ △DAC
4、证明线段的乘积问题可转化为线段的比例问题
ABDC3、如图:在Rt △ ABC中, ∠ABC=900,BD⊥AC于D ABDCEF问:若E是BC中点,ED的延长线交BA的延长线于F,
求证:AB : BC=DF : BF
