27.2.2 相似三角形应用举例(1)(含答案)[下学期]
文档属性
| 名称 | 27.2.2 相似三角形应用举例(1)(含答案)[下学期] |
|
|
| 格式 | rar | ||
| 文件大小 | 59.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-01-04 23:06:00 | ||
图片预览

文档简介
27.2.2 相似三角形应用举例(1) ( http: / / )
新颖题赏析
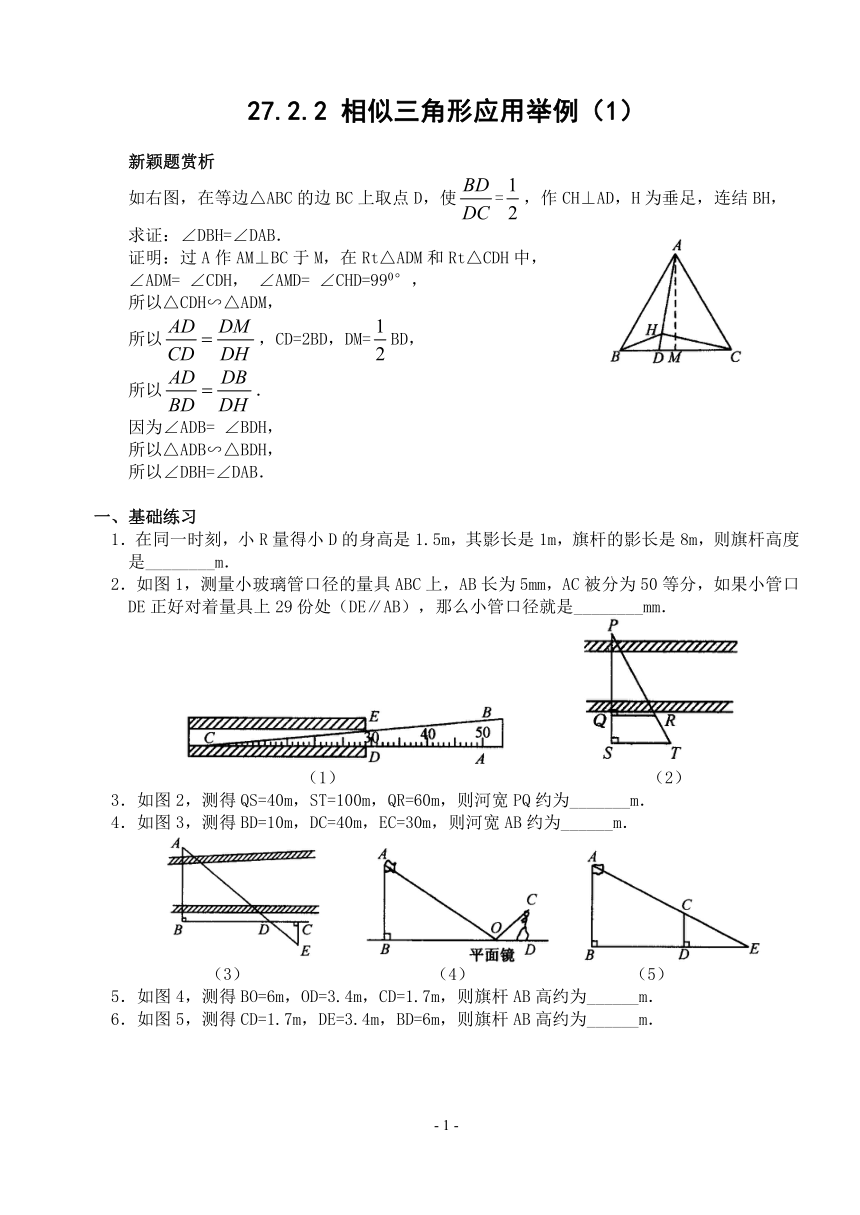
如右图,在等边△ABC的边BC上取点D,使=,作CH⊥AD,H为垂足,连结BH,
求证:∠DBH=∠DAB.
证明:过A作AM⊥BC于M,在Rt△ADM和Rt△CDH中,
∠ADM=∠CDH,∠AMD=∠CHD=990°,
所以△CDH∽△ADM,
所以,CD=2BD,DM=BD,
所以.
因为∠ADB=∠BDH,
所以△ADB∽△BDH,
所以∠DBH=∠DAB.
一、基础练习
1.在同一时刻,小R量得小D的身高是1.5m,其影长是1m,旗杆的影长是8m,则旗杆高度是________m.
2.如图1,测量小玻璃管口径的量具ABC上,AB长为5mm,AC被分为50等分,如果小管口DE正好对着量具上29份处(DE∥AB),那么小管口径就是________mm.
(1) (2)
3.如图2,测得QS=40m,ST=100m,QR=60m,则河宽PQ约为_______m.
4.如图3,测得BD=10m,DC=40m,EC=30m,则河宽AB约为______m.
(3) (4) (5)
5.如图4,测得BO=6m,OD=3.4m,CD=1.7m,则旗杆AB高约为______m.
6.如图5,测得CD=1.7m,DE=3.4m,BD=6m,则旗杆AB高约为______m.
7.将两块完全相同的等腰直角三角形的三角板摆放如图6,假设图形中的所有的点,线都在同一平面内,则图形中相似但又不全等的三角形是________.
(6) (7)
8.如图7,请你设计几种不同的方法,将一个Rt△ABC分割成四个小三角形,使得每一个小三角形都与原直角三角形相似. 设计好以后,请你想一想 ( http: / / )
设计好以后,请你想一想,将一个锐角△ABC(或钝角三角形)分割成四个小三角形,使得每一个小三角形都与原直角三角形相似,你能够吗?
二、整合练习
1.图中的每一个小正方形的边长为1,将三个正方形并排组成一个矩形.
(1)求证:△BCE∽△BED;(2)求证:∠BEC+∠BED=45°
2.如图,ABCD是边长为3的正方形,E是BC边上一点,且EC=2BE,将正方形折叠,使点A与点E重合,折痕为MN,若四边 ( http: / / )形BCMN的面积和四边形ADMN的面积分别为S1和S2,求S1:S2.
答案:
一、基础练习
1.12 2.2.9 3.60 4.7.5
5.3(∠AOB=∠COD) 6.4.7
7.△BDE∽△CDB∽△ABE8.图(1)、(2)分别取斜边和直 ( http: / / )
8.图(1)、(2)分别取斜边和直角边的中点,结果分割成四个小三角形均全等,分别与原三角形相似.图(3)、(4)、(5)、(6)、(7)依次作直角三角形斜边上的高.当△ABC由Rt△变成锐角三角形或钝角三角形时,只要顺次连结原三角形三边的中点所得的图形符合要求.如图(8)、(9).(运用依次作直角三角形斜边上的高的方法,可将Rt△分成n个小三角形其每一个小三角形都与原直角三角形相似)
二、整合练习
1.(1)在△BCE和△BED中,BE=,BC=1,BD=2,
因为∠CBE=∠EBD.,所以△BCE∽△BED.
(2)因为△BCE∽△BED,所以∠BCE=∠BED,∠BEC+∠BED=∠BEC+∠BCE=∠ABE=45°
2.设MN与AE相交于点F,BC=3,EC=2BE=2,BE=1,AE=,MN垂直平分AE,
△AFM∽△ABE,,AM=AE2=,BM=,
过N作NH⊥AB于H,△MNH≌△EAB.MH=BE=1,DN=-1=,NC=,
S1:S2=(+):(+)=11:7.
又解:设AM=ME=x,BM=3-x,x2=(3-x)2+1,6x=10,x=,
设DN=y,NE2=9+y2=9-6y+y2+4,y=,S2=·=,S1=9-=,S1:S2=11:7.
- 1 -
新颖题赏析
如右图,在等边△ABC的边BC上取点D,使=,作CH⊥AD,H为垂足,连结BH,
求证:∠DBH=∠DAB.
证明:过A作AM⊥BC于M,在Rt△ADM和Rt△CDH中,
∠ADM=∠CDH,∠AMD=∠CHD=990°,
所以△CDH∽△ADM,
所以,CD=2BD,DM=BD,
所以.
因为∠ADB=∠BDH,
所以△ADB∽△BDH,
所以∠DBH=∠DAB.
一、基础练习
1.在同一时刻,小R量得小D的身高是1.5m,其影长是1m,旗杆的影长是8m,则旗杆高度是________m.
2.如图1,测量小玻璃管口径的量具ABC上,AB长为5mm,AC被分为50等分,如果小管口DE正好对着量具上29份处(DE∥AB),那么小管口径就是________mm.
(1) (2)
3.如图2,测得QS=40m,ST=100m,QR=60m,则河宽PQ约为_______m.
4.如图3,测得BD=10m,DC=40m,EC=30m,则河宽AB约为______m.
(3) (4) (5)
5.如图4,测得BO=6m,OD=3.4m,CD=1.7m,则旗杆AB高约为______m.
6.如图5,测得CD=1.7m,DE=3.4m,BD=6m,则旗杆AB高约为______m.
7.将两块完全相同的等腰直角三角形的三角板摆放如图6,假设图形中的所有的点,线都在同一平面内,则图形中相似但又不全等的三角形是________.
(6) (7)
8.如图7,请你设计几种不同的方法,将一个Rt△ABC分割成四个小三角形,使得每一个小三角形都与原直角三角形相似. 设计好以后,请你想一想 ( http: / / )
设计好以后,请你想一想,将一个锐角△ABC(或钝角三角形)分割成四个小三角形,使得每一个小三角形都与原直角三角形相似,你能够吗?
二、整合练习
1.图中的每一个小正方形的边长为1,将三个正方形并排组成一个矩形.
(1)求证:△BCE∽△BED;(2)求证:∠BEC+∠BED=45°
2.如图,ABCD是边长为3的正方形,E是BC边上一点,且EC=2BE,将正方形折叠,使点A与点E重合,折痕为MN,若四边 ( http: / / )形BCMN的面积和四边形ADMN的面积分别为S1和S2,求S1:S2.
答案:
一、基础练习
1.12 2.2.9 3.60 4.7.5
5.3(∠AOB=∠COD) 6.4.7
7.△BDE∽△CDB∽△ABE8.图(1)、(2)分别取斜边和直 ( http: / / )
8.图(1)、(2)分别取斜边和直角边的中点,结果分割成四个小三角形均全等,分别与原三角形相似.图(3)、(4)、(5)、(6)、(7)依次作直角三角形斜边上的高.当△ABC由Rt△变成锐角三角形或钝角三角形时,只要顺次连结原三角形三边的中点所得的图形符合要求.如图(8)、(9).(运用依次作直角三角形斜边上的高的方法,可将Rt△分成n个小三角形其每一个小三角形都与原直角三角形相似)
二、整合练习
1.(1)在△BCE和△BED中,BE=,BC=1,BD=2,
因为∠CBE=∠EBD.,所以△BCE∽△BED.
(2)因为△BCE∽△BED,所以∠BCE=∠BED,∠BEC+∠BED=∠BEC+∠BCE=∠ABE=45°
2.设MN与AE相交于点F,BC=3,EC=2BE=2,BE=1,AE=,MN垂直平分AE,
△AFM∽△ABE,,AM=AE2=,BM=,
过N作NH⊥AB于H,△MNH≌△EAB.MH=BE=1,DN=-1=,NC=,
S1:S2=(+):(+)=11:7.
又解:设AM=ME=x,BM=3-x,x2=(3-x)2+1,6x=10,x=,
设DN=y,NE2=9+y2=9-6y+y2+4,y=,S2=·=,S1=9-=,S1:S2=11:7.
- 1 -
