2022-2023年人教版(2019)新教材高中物理必修2 第7章万有引力与宇宙航行第1节行星的运动(3)课件(共27张PPT)
文档属性
| 名称 | 2022-2023年人教版(2019)新教材高中物理必修2 第7章万有引力与宇宙航行第1节行星的运动(3)课件(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-11-09 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
行星的运动
明月几时有?把酒问青天。不知天上宫阙,今夕是何年。
课堂引入:
课堂引入:
人们仰望星空,遐想无限。天体的运行有没有可循的规律呢?
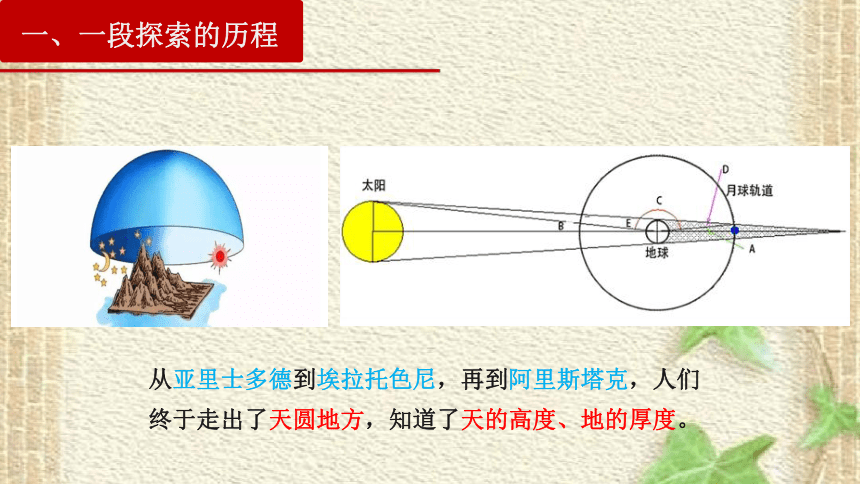
一、一段探索的历程
从亚里士多德到埃拉托色尼,再到阿里斯塔克,人们终于走出了天圆地方,知道了天的高度、地的厚度。
二、两种学说的碰撞
地
心
说
日
心
说
二、两种学说的碰撞
代表人物:托 勒 密
地球是宇宙的中心,并且静止不动,一切行星围绕地球做圆周运动。
地
心
说
“地心说”的不足
随着人们对天体运动的不断研究,发现“地心说”所描述的天体的运动不仅复杂而且问题很多。如果把地球从天体运动的中心位置移到一个普通的、绕太阳运动的行星的位置,换一个角度来考虑天体的运动,许多问题都可以解决,行星运动的描述也变得简单了。
二、两种学说的碰撞
代表人物:哥白尼
太阳是宇宙的中心,并且静止不动,一切行星都围绕太阳运动。
日
心
说
二、两种学说的碰撞
“日心说”相对“地心说”能更完美地解释天体的运动,但它并没有在天文测算的精确度上有多大的提高。 其后,许多天文学家对天体运动进行不断的探索、完善,建立了最初的天体运动理论。近代早期最重要的观测工作是由丹麦的第谷进行的。
【观测大师:第谷】
哥白尼之后,第谷连续20年对行星的位置进行了较仔细的测量,大大提高了测量的精确程度。在第谷之前,人们测量天体位置的误差大约是10’,第谷把这个不确定性减小到2’。得出行星绕太阳做匀速圆周运动的模型。
“日心说”最终战胜“地心说”的科学功臣。
第谷(1546-1601)
【数学天才:开普勒】
德国的物理学家开普勒继承和总结了他的导师第谷的全部观测资料及数据,他得到的结果与第谷的观察数据相差8’,而当时第谷公认的误差为2’。开普勒经过20年的研究和四年多的刻苦计算,先后否定了19种设想,最后终于计算出行星绕太阳运动的轨迹为椭圆,并总结为行星运动三大定律。
三、开普勒行星运动定律
所有的行星围绕太阳运动的轨道都是椭圆,太阳处在所有椭圆的一个焦点上。
1.开普勒第一定律:
说明:(1)太阳并不是位于椭圆中心,而是位于焦点处。
(2)不同行星轨道不同,但所有轨道的焦点重合。
【轨道定律】
做一做
椭圆上某点到两个焦点的距离之和与椭圆上另一点到两焦点的距离之和有什么关系
思维拓展:把细绳的两端合在一起(即两个焦点合并成一个点),再用铅笔把细绳拉紧,在板上画出的图形是什么?
想一想
三、开普勒行星运动定律
对于任意一个行星而言,它和太阳的连线在相等的时间内扫过相等的面积。
2.开普勒第二定律:
说明:行星在近日点速率大于远日点速率。
【面积定律】
春夏两季(186天)比秋冬两季(179天)要长。
你认为春夏两季的时间长还是秋冬两季的时间长?
【学以致用】
三、开普勒行星运动定律
所有行星轨道的半长轴的三次方跟它的公转周期的二次方的比都相等。
3.开普勒第三定律:
猜想:a3/T2=k,你能猜出k可能跟谁有关吗 行星?太阳?
【周期定律】
行星/卫星 半长轴(106km) 周期(天) k(m /s )
水星 57 87.97
金星 108 225
地球 149 365
火星 228 687
木星 778 4333
土星 1426 10759
天王星 2870 30660
海王星 4498 60148
月球 0.3844 27.3
同步卫星 0.0424 1
3.36×10^18
3.36×10^18
3.36×10^18
3.36×10^18
3.36×10^18
3.36×10^18
3.37×10^18
3.37×10^18
1.03×10^13
1.03×10^13
【验证猜想】
结论:
(1)开普勒第三定律也适用于太阳系以外的其他环绕系统, 不同的环绕系统,k值不同。
(2)k值与环绕天体无关,由中心天体决定。
行星运动的近似处理方法
实际上,行星的轨道与圆十分接近(图 7.1-3),在中学阶段的研究中我们可按圆轨道处理。
行星运动的近似处理方法
1.行星绕太阳运动的轨道近似为圆,太阳处于圆心。
2.行星绕太阳做匀速圆周运动。
3.所有行星轨道半径的三次方与它的公转周期的二次方的比值都相等,即
曲折的历程:
哥白尼勇于挑战权威、布鲁诺为捍卫真理走上火刑架、第谷坚持观测20多年、伽利略被终身监禁而矢志不移、开普勒贫病交加而最终死在讨薪的路上、、、、、
但科学家们面对困难不屈不挠的科学态度和追求科学真理的崇高理想在永世流传。
课堂小结:
【典例1】人类一直不断地对宇宙追求探索着,关于宇宙天体学说正确的是( )
A.日心说代表人物是托勒密
B.地心说是正确的,日心说是错误的
C.日心说被人们所接受的原因是以太阳为中心,许多问题都可以解决,行星运动也变得简单了
D.太阳从东边升起,从西边落下,所以太阳绕地球运动
典例分析
【正确答案】C
【典例2】如图所示,火星和地球都在围绕着太阳旋转,其运行轨道是椭圆。根据开普勒行星运动定律可知( )
A.太阳位于地球运行轨道的中心
B.地球靠近太阳的过程中,运行速率减小
C.火星远离太阳的过程中,它与太阳的连线在相等时间内扫过的面积逐渐增大
D.火星绕太阳运行一周的时间比地球的长
典例分析
【正确答案】D
【典例3】(多选)下列对开普勒第三定律 的理解,正确的是( )
A.T表示行星的自转周期
B.k是一个仅与中心天体有关的常量
C.该定律既适用于行星绕太阳的运动,也适用于卫星绕行星的运动
D.若地球绕太阳运转的半长轴为a1,周期为T1,月球绕地球运转的半长轴为a2,周期为T2,由开普勒第三定律可得
典例分析
【正确答案】BC
【典例4】为了探测引力波,“天琴计划”预计发射地球卫星P,其轨道半径约为地球半径的16倍;另一地球卫星Q的轨道半径约为地球半径的4倍。P与Q的周期之比约为( )
A.2∶1 B.4∶1 C.8∶1 D.16∶1
典例分析
【正确答案】C
【典例5】已知木星绕太阳的公转周期是地球绕太阳公转周期的12倍,则木星轨道半长轴是地球轨道半长轴的多少倍?
典例分析
【解析】根据开普勒第三定律有:
开普勒完美解决了“行星怎样运动?”的问题,为此他本人也被誉为“天空的立法者”。
请思考:行星为什么会按照开普勒描述的三定律那样
运动?要想知道结果,请预习下节课的内容。
预习与思考:
行星的运动
明月几时有?把酒问青天。不知天上宫阙,今夕是何年。
课堂引入:
课堂引入:
人们仰望星空,遐想无限。天体的运行有没有可循的规律呢?
一、一段探索的历程
从亚里士多德到埃拉托色尼,再到阿里斯塔克,人们终于走出了天圆地方,知道了天的高度、地的厚度。
二、两种学说的碰撞
地
心
说
日
心
说
二、两种学说的碰撞
代表人物:托 勒 密
地球是宇宙的中心,并且静止不动,一切行星围绕地球做圆周运动。
地
心
说
“地心说”的不足
随着人们对天体运动的不断研究,发现“地心说”所描述的天体的运动不仅复杂而且问题很多。如果把地球从天体运动的中心位置移到一个普通的、绕太阳运动的行星的位置,换一个角度来考虑天体的运动,许多问题都可以解决,行星运动的描述也变得简单了。
二、两种学说的碰撞
代表人物:哥白尼
太阳是宇宙的中心,并且静止不动,一切行星都围绕太阳运动。
日
心
说
二、两种学说的碰撞
“日心说”相对“地心说”能更完美地解释天体的运动,但它并没有在天文测算的精确度上有多大的提高。 其后,许多天文学家对天体运动进行不断的探索、完善,建立了最初的天体运动理论。近代早期最重要的观测工作是由丹麦的第谷进行的。
【观测大师:第谷】
哥白尼之后,第谷连续20年对行星的位置进行了较仔细的测量,大大提高了测量的精确程度。在第谷之前,人们测量天体位置的误差大约是10’,第谷把这个不确定性减小到2’。得出行星绕太阳做匀速圆周运动的模型。
“日心说”最终战胜“地心说”的科学功臣。
第谷(1546-1601)
【数学天才:开普勒】
德国的物理学家开普勒继承和总结了他的导师第谷的全部观测资料及数据,他得到的结果与第谷的观察数据相差8’,而当时第谷公认的误差为2’。开普勒经过20年的研究和四年多的刻苦计算,先后否定了19种设想,最后终于计算出行星绕太阳运动的轨迹为椭圆,并总结为行星运动三大定律。
三、开普勒行星运动定律
所有的行星围绕太阳运动的轨道都是椭圆,太阳处在所有椭圆的一个焦点上。
1.开普勒第一定律:
说明:(1)太阳并不是位于椭圆中心,而是位于焦点处。
(2)不同行星轨道不同,但所有轨道的焦点重合。
【轨道定律】
做一做
椭圆上某点到两个焦点的距离之和与椭圆上另一点到两焦点的距离之和有什么关系
思维拓展:把细绳的两端合在一起(即两个焦点合并成一个点),再用铅笔把细绳拉紧,在板上画出的图形是什么?
想一想
三、开普勒行星运动定律
对于任意一个行星而言,它和太阳的连线在相等的时间内扫过相等的面积。
2.开普勒第二定律:
说明:行星在近日点速率大于远日点速率。
【面积定律】
春夏两季(186天)比秋冬两季(179天)要长。
你认为春夏两季的时间长还是秋冬两季的时间长?
【学以致用】
三、开普勒行星运动定律
所有行星轨道的半长轴的三次方跟它的公转周期的二次方的比都相等。
3.开普勒第三定律:
猜想:a3/T2=k,你能猜出k可能跟谁有关吗 行星?太阳?
【周期定律】
行星/卫星 半长轴(106km) 周期(天) k(m /s )
水星 57 87.97
金星 108 225
地球 149 365
火星 228 687
木星 778 4333
土星 1426 10759
天王星 2870 30660
海王星 4498 60148
月球 0.3844 27.3
同步卫星 0.0424 1
3.36×10^18
3.36×10^18
3.36×10^18
3.36×10^18
3.36×10^18
3.36×10^18
3.37×10^18
3.37×10^18
1.03×10^13
1.03×10^13
【验证猜想】
结论:
(1)开普勒第三定律也适用于太阳系以外的其他环绕系统, 不同的环绕系统,k值不同。
(2)k值与环绕天体无关,由中心天体决定。
行星运动的近似处理方法
实际上,行星的轨道与圆十分接近(图 7.1-3),在中学阶段的研究中我们可按圆轨道处理。
行星运动的近似处理方法
1.行星绕太阳运动的轨道近似为圆,太阳处于圆心。
2.行星绕太阳做匀速圆周运动。
3.所有行星轨道半径的三次方与它的公转周期的二次方的比值都相等,即
曲折的历程:
哥白尼勇于挑战权威、布鲁诺为捍卫真理走上火刑架、第谷坚持观测20多年、伽利略被终身监禁而矢志不移、开普勒贫病交加而最终死在讨薪的路上、、、、、
但科学家们面对困难不屈不挠的科学态度和追求科学真理的崇高理想在永世流传。
课堂小结:
【典例1】人类一直不断地对宇宙追求探索着,关于宇宙天体学说正确的是( )
A.日心说代表人物是托勒密
B.地心说是正确的,日心说是错误的
C.日心说被人们所接受的原因是以太阳为中心,许多问题都可以解决,行星运动也变得简单了
D.太阳从东边升起,从西边落下,所以太阳绕地球运动
典例分析
【正确答案】C
【典例2】如图所示,火星和地球都在围绕着太阳旋转,其运行轨道是椭圆。根据开普勒行星运动定律可知( )
A.太阳位于地球运行轨道的中心
B.地球靠近太阳的过程中,运行速率减小
C.火星远离太阳的过程中,它与太阳的连线在相等时间内扫过的面积逐渐增大
D.火星绕太阳运行一周的时间比地球的长
典例分析
【正确答案】D
【典例3】(多选)下列对开普勒第三定律 的理解,正确的是( )
A.T表示行星的自转周期
B.k是一个仅与中心天体有关的常量
C.该定律既适用于行星绕太阳的运动,也适用于卫星绕行星的运动
D.若地球绕太阳运转的半长轴为a1,周期为T1,月球绕地球运转的半长轴为a2,周期为T2,由开普勒第三定律可得
典例分析
【正确答案】BC
【典例4】为了探测引力波,“天琴计划”预计发射地球卫星P,其轨道半径约为地球半径的16倍;另一地球卫星Q的轨道半径约为地球半径的4倍。P与Q的周期之比约为( )
A.2∶1 B.4∶1 C.8∶1 D.16∶1
典例分析
【正确答案】C
【典例5】已知木星绕太阳的公转周期是地球绕太阳公转周期的12倍,则木星轨道半长轴是地球轨道半长轴的多少倍?
典例分析
【解析】根据开普勒第三定律有:
开普勒完美解决了“行星怎样运动?”的问题,为此他本人也被誉为“天空的立法者”。
请思考:行星为什么会按照开普勒描述的三定律那样
运动?要想知道结果,请预习下节课的内容。
预习与思考:
