相似三角形的判定定理2[下学期]
文档属性
| 名称 | 相似三角形的判定定理2[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-01-21 17:02:00 | ||
图片预览

文档简介
课件19张PPT。相似三角形的判定定理2(2)∵DE∥BC
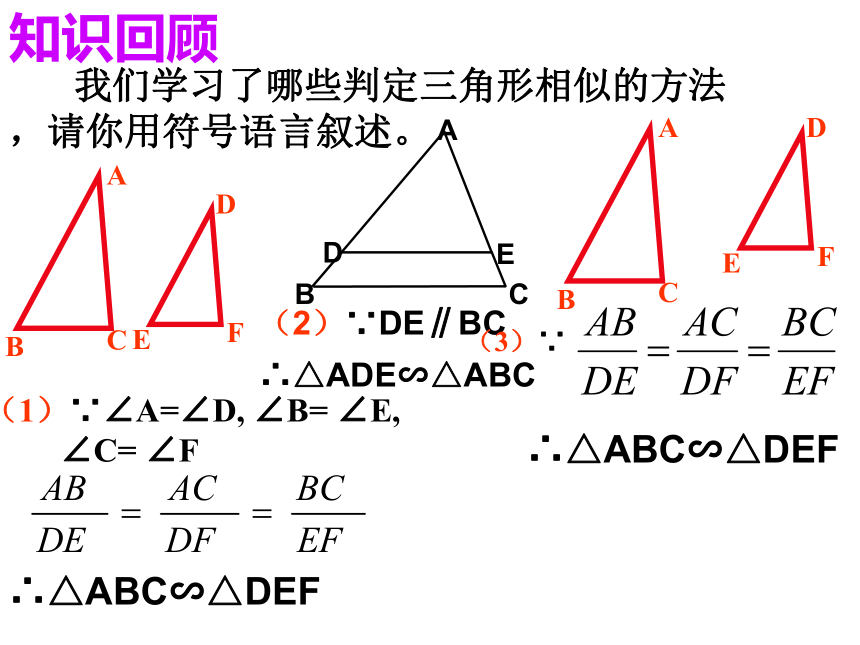
∴△ADE∽△ABC 我们学习了哪些判定三角形相似的方法,请你用符号语言叙述。知识回顾(1)∵∠A=∠D, ∠B= ∠E,
∠C= ∠F∴△ABC∽△DEF(3)∵∴△ABC∽△DEF1.根据下列条件,判断△ABC和△A’B’C’是否相似,并说明理由:
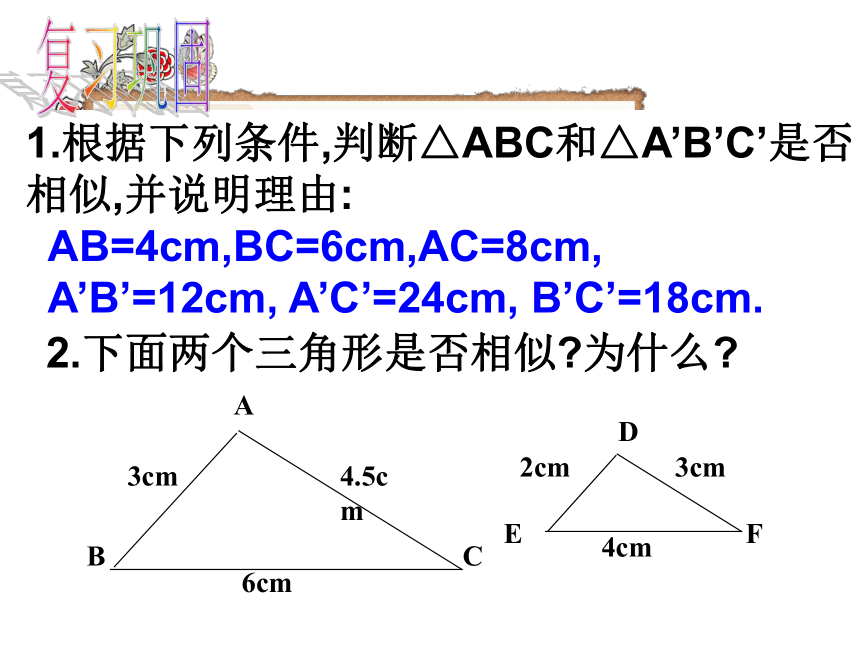
AB=4cm,BC=6cm,AC=8cm,
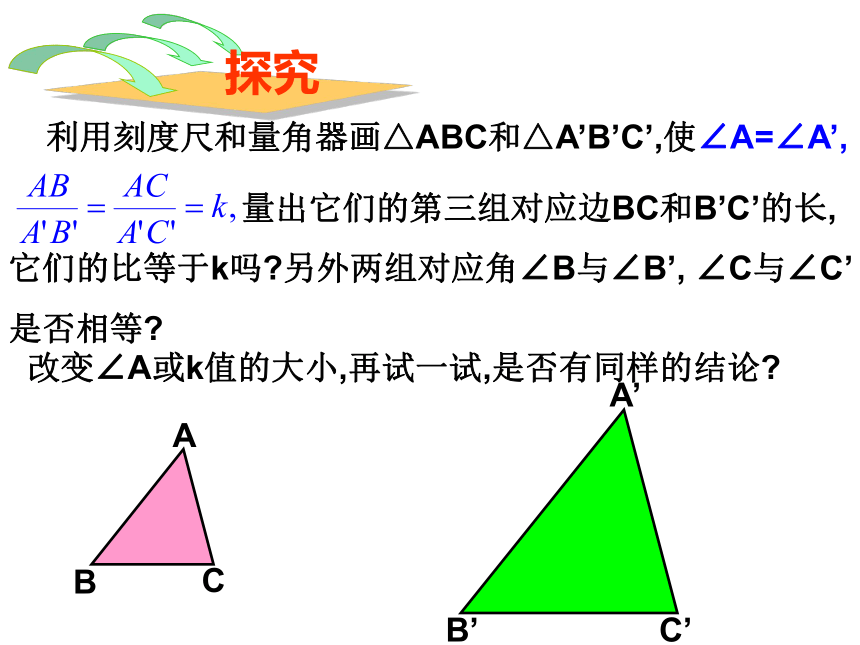
A’B’=12cm, A’C’=24cm, B’C’=18cm.复习巩固2.下面两个三角形是否相似?为什么? 利用刻度尺和量角器画△ABC和△A’B’C’,使∠A=∠A’, 量出它们的第三组对应边BC和B’C’的长,它们的比等于k吗?另外两组对应角∠B与∠B’, ∠C与∠C’是否相等?
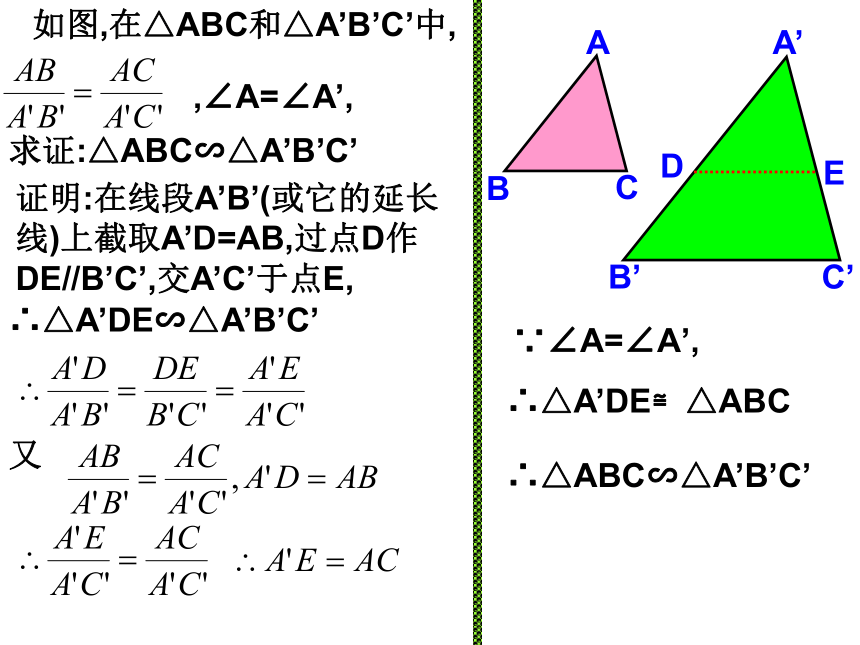
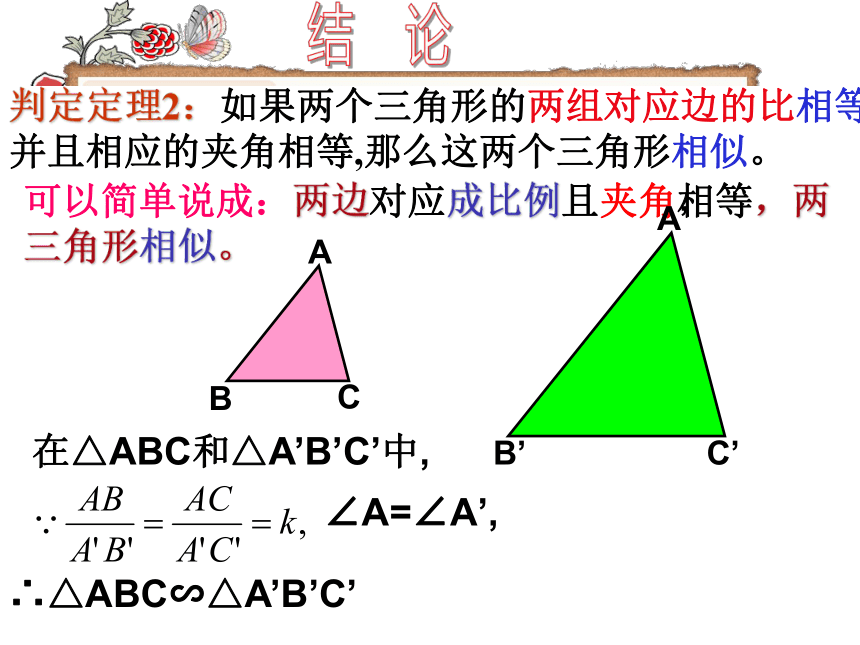
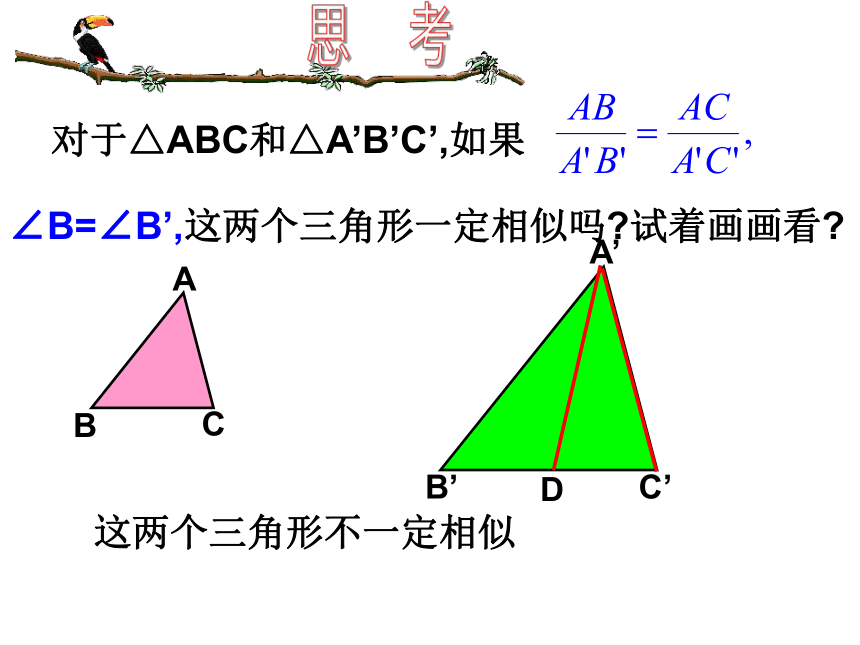
改变∠A或k值的大小,再试一试,是否有同样的结论?如图,在△ABC和△A’B’C’中,求证:△ABC∽△A’B’C’证明:在线段A’B’(或它的延长线)上截取A’D=AB,过点D作DE//B’C’,交A’C’于点E,DE∴△A’DE∽△A’B’C’又∵∠A=∠A’,∴△A’DE≌△ABC∴△ABC∽△A’B’C’,∠A=∠A’,判定定理2:如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似。结 论可以简单说成:两边对应成比例且夹角相等,两三角形相似。在△ABC和△A’B’C’中,∴△ABC∽△A’B’C’∠A=∠A’,思 考 对于△ABC和△A’B’C’,如果
∠B=∠B’,这两个三角形一定相似吗?试着画画看?
这两个三角形不一定相似D例 题 讲 解例1 根据下列条件,判断△ABC和△A’B’C’是否相似,并说明理由:
∠A=120°,AB=7cm,AC=14cm,
∠A’=120°,A’B’=3cm,A’C’=6cm,
例2.如图,在△ABC中,D在AC上,已知AD=2 cm,AB=4cm,AC=8cm, 求证:△ABD∽△ABC. 例3. 如图,在正方形ABCD中,已知P是BC上的点,且BP=3PC,Q是CD的中点,试判断△ADQ∽△QCP吗?说明理由.这是探索结论的题型,要先观察,猜测例 4. 如图矩形ABCD是由三个正方形ABEG,GEFH,HFCD组成的,找出图中的相似三角形.解:△ AEF∽ △CEA.理由是:
设小正方形的边长是1,由勾股定理得∵∠ AEF = ∠CEA=135°.∴△ AEF ∽ △CEA.1.如下图所示,在△ABC中,D﹑E分别在AC﹑AB上,
且AD:AB=AE:AC=1:2,BC=5,则DE=________ 练一练2.如图,在4×4的正方形方格中,△ABC和△DEF
的顶点都在边长为1的小正方形的顶点上.
(1)填空:∠ABC= °, ∠DEF= ° ;
(2)判断△ABC与△DEF是否相似,并证明你的结论.3.已知零件的外径为25cm,要求它的厚度x,
需先求出它的内孔直径AB,现用一个交叉卡钳
(AC和BD的长相等)去量(如图),
若OA:OC=OB:OD=3,CD=7cm。求此零件的厚度x。注意审题,题中没有平行条件4.下列说法中错误的是( )
(A)有一个角是30°的两个等腰三角形相似
(B)有一个角是60°的两个等腰三角形相似
(C)有一个角是90°的两个等腰三角形相似
(D)有一个角是120°的两个等腰三角形相似
5.如图,在正方形网格上有6个斜三角形:①△ABC
②△BCD;③△BDE;④△BFG;⑤△FGH;⑥△EKF。
其中②~⑥中与三角形①相似的三角形是_____________K6.如图,Rt△ABC,D、E是BC上两点,
且AB=BD=DE=EC,请问:此图中共有几个三角形?
是否存在相似三角形?如果有请你指出来,并加以证明.7.已知,如图,O点在△ABC内部,连AO、BO、CO,
A’、B’、C’分别在AO、BO、CO上,且AB∥A’B’、
BC∥B’C’.⑴求证:△OAC∽△OA’C’.
⑵若将图⑴中的O点移至△ABC外,如图,
其它条件不变,题中要求证的结论成立吗?
①在图⑵基础上画出相应的图形,观察并回答
答: (填成立或不成立).
②证明你在①中观察到的结论.A′C′B′思考还有其它的结论吗?想一想在△ABC中,D﹑E分别在AB﹑AC上,请你加一个条件使△ADE∽△ABC,这个条件可以是___________相信你一定行!DE∥BC本节课你有什么收获?不经历风雨,怎么见彩虹没有人能随随便便成功!再见
∴△ADE∽△ABC 我们学习了哪些判定三角形相似的方法,请你用符号语言叙述。知识回顾(1)∵∠A=∠D, ∠B= ∠E,
∠C= ∠F∴△ABC∽△DEF(3)∵∴△ABC∽△DEF1.根据下列条件,判断△ABC和△A’B’C’是否相似,并说明理由:
AB=4cm,BC=6cm,AC=8cm,
A’B’=12cm, A’C’=24cm, B’C’=18cm.复习巩固2.下面两个三角形是否相似?为什么? 利用刻度尺和量角器画△ABC和△A’B’C’,使∠A=∠A’, 量出它们的第三组对应边BC和B’C’的长,它们的比等于k吗?另外两组对应角∠B与∠B’, ∠C与∠C’是否相等?
改变∠A或k值的大小,再试一试,是否有同样的结论?如图,在△ABC和△A’B’C’中,求证:△ABC∽△A’B’C’证明:在线段A’B’(或它的延长线)上截取A’D=AB,过点D作DE//B’C’,交A’C’于点E,DE∴△A’DE∽△A’B’C’又∵∠A=∠A’,∴△A’DE≌△ABC∴△ABC∽△A’B’C’,∠A=∠A’,判定定理2:如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似。结 论可以简单说成:两边对应成比例且夹角相等,两三角形相似。在△ABC和△A’B’C’中,∴△ABC∽△A’B’C’∠A=∠A’,思 考 对于△ABC和△A’B’C’,如果
∠B=∠B’,这两个三角形一定相似吗?试着画画看?
这两个三角形不一定相似D例 题 讲 解例1 根据下列条件,判断△ABC和△A’B’C’是否相似,并说明理由:
∠A=120°,AB=7cm,AC=14cm,
∠A’=120°,A’B’=3cm,A’C’=6cm,
例2.如图,在△ABC中,D在AC上,已知AD=2 cm,AB=4cm,AC=8cm, 求证:△ABD∽△ABC. 例3. 如图,在正方形ABCD中,已知P是BC上的点,且BP=3PC,Q是CD的中点,试判断△ADQ∽△QCP吗?说明理由.这是探索结论的题型,要先观察,猜测例 4. 如图矩形ABCD是由三个正方形ABEG,GEFH,HFCD组成的,找出图中的相似三角形.解:△ AEF∽ △CEA.理由是:
设小正方形的边长是1,由勾股定理得∵∠ AEF = ∠CEA=135°.∴△ AEF ∽ △CEA.1.如下图所示,在△ABC中,D﹑E分别在AC﹑AB上,
且AD:AB=AE:AC=1:2,BC=5,则DE=________ 练一练2.如图,在4×4的正方形方格中,△ABC和△DEF
的顶点都在边长为1的小正方形的顶点上.
(1)填空:∠ABC= °, ∠DEF= ° ;
(2)判断△ABC与△DEF是否相似,并证明你的结论.3.已知零件的外径为25cm,要求它的厚度x,
需先求出它的内孔直径AB,现用一个交叉卡钳
(AC和BD的长相等)去量(如图),
若OA:OC=OB:OD=3,CD=7cm。求此零件的厚度x。注意审题,题中没有平行条件4.下列说法中错误的是( )
(A)有一个角是30°的两个等腰三角形相似
(B)有一个角是60°的两个等腰三角形相似
(C)有一个角是90°的两个等腰三角形相似
(D)有一个角是120°的两个等腰三角形相似
5.如图,在正方形网格上有6个斜三角形:①△ABC
②△BCD;③△BDE;④△BFG;⑤△FGH;⑥△EKF。
其中②~⑥中与三角形①相似的三角形是_____________K6.如图,Rt△ABC,D、E是BC上两点,
且AB=BD=DE=EC,请问:此图中共有几个三角形?
是否存在相似三角形?如果有请你指出来,并加以证明.7.已知,如图,O点在△ABC内部,连AO、BO、CO,
A’、B’、C’分别在AO、BO、CO上,且AB∥A’B’、
BC∥B’C’.⑴求证:△OAC∽△OA’C’.
⑵若将图⑴中的O点移至△ABC外,如图,
其它条件不变,题中要求证的结论成立吗?
①在图⑵基础上画出相应的图形,观察并回答
答: (填成立或不成立).
②证明你在①中观察到的结论.A′C′B′思考还有其它的结论吗?想一想在△ABC中,D﹑E分别在AB﹑AC上,请你加一个条件使△ADE∽△ABC,这个条件可以是___________相信你一定行!DE∥BC本节课你有什么收获?不经历风雨,怎么见彩虹没有人能随随便便成功!再见
