相似三角形判定综合应用.[下学期]
文档属性
| 名称 | 相似三角形判定综合应用.[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-27 00:00:00 | ||
图片预览



文档简介
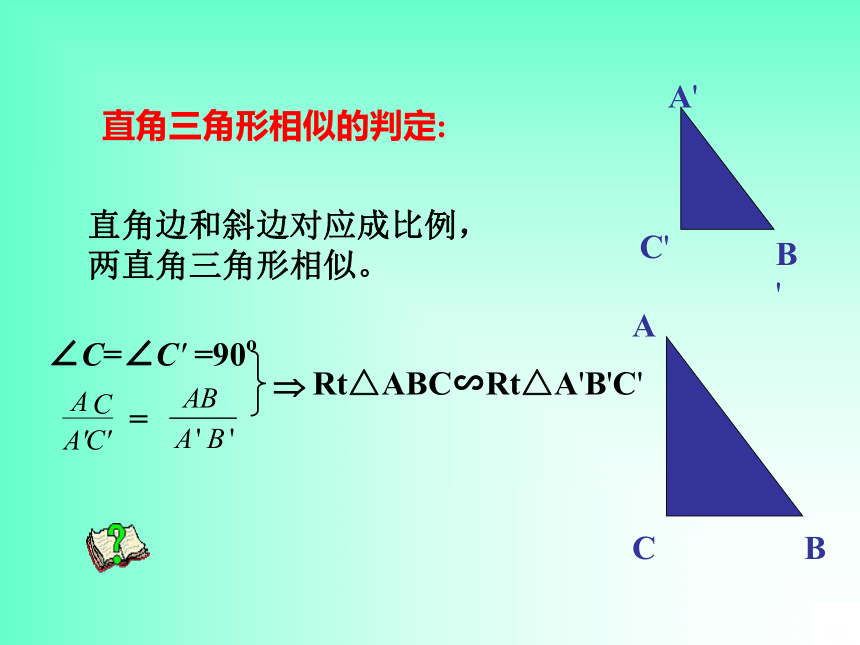
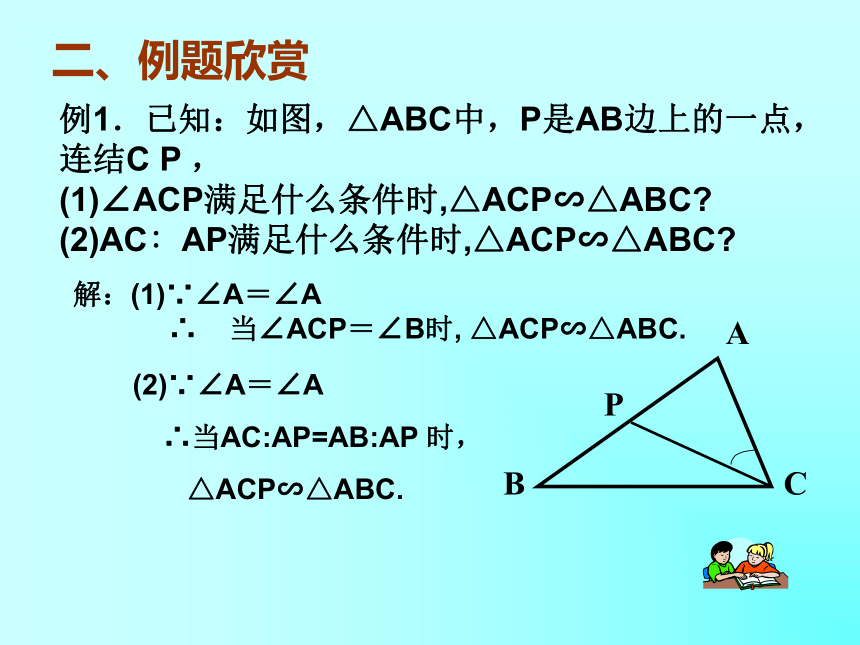
课件13张PPT。相似三角形的判定(4)相似三角形的判定(4)相似三角形的判定定理:定理1:两角对应相等,两三角形相似。定理2:两边对应成比例且夹角相等,两三角形相似。定理3:三边对应成比例,两三角形相似。一、知识回顾解:(1)∵∠A=∠A
∴ 当∠ACP=∠B时, △ACP∽△ABC. (2)∵∠A=∠A
∴当AC:AP=AB:AP 时,
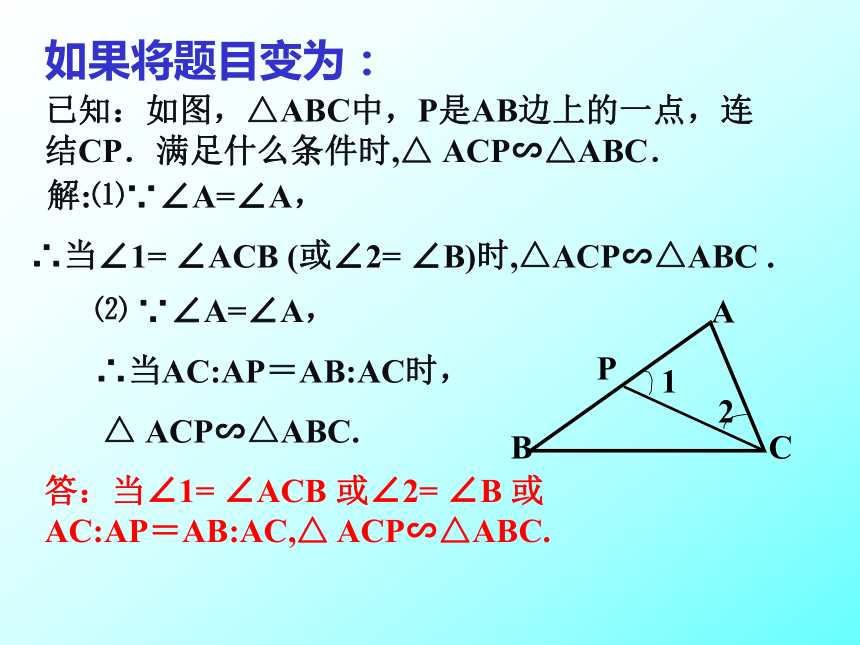
△ACP∽△ABC.答:当∠1= ∠ACB 或∠2= ∠B 或AC:AP=AB:AC,△ ACP∽△ABC. 解:⑴∵∠A=∠A,
∴当∠1= ∠ACB (或∠2= ∠B)时,△ACP∽△ABC .如果将题目变为:⑵ ∵∠A=∠A,
∴当AC:AP=AB:AC时,
△ ACP∽△ABC.三、随堂练习1、EE已知,△ABC中,D为AB上一点,画一条过点D的直线(不与AB重合),交AC于E,使所得三角形与原三角形相似,这样的直线最多能画出多少条? 已知,△ABC中,D为AB上一点,画一条过点D的直线(不与AB重合),交另一边于E,使所得三角形与原三角形相似,这样的直线最多能画出多少条?如果将题目变为:EEEEEE四、中考透视1、如图正方形边长是2,BE=CE,MN=1。线段MN的两端在CD、AD上滑动,当DM为多长时,△ABE与以D、M、N为顶点的三角形相似。N 2、已知在△ABC中,∠C=90o ,AC=8cm,BC=6cm,点P从点A出发,沿AC以3厘米/秒的速度向点C移动,点Q从点B出发,沿BA以4厘米/秒的速度向点A移动。
如果P、Q分别从A、B 同时出发,移动时间为t秒 (02、练习册,相似三角形的判定4谢谢大家!
∴ 当∠ACP=∠B时, △ACP∽△ABC. (2)∵∠A=∠A
∴当AC:AP=AB:AP 时,
△ACP∽△ABC.答:当∠1= ∠ACB 或∠2= ∠B 或AC:AP=AB:AC,△ ACP∽△ABC. 解:⑴∵∠A=∠A,
∴当∠1= ∠ACB (或∠2= ∠B)时,△ACP∽△ABC .如果将题目变为:⑵ ∵∠A=∠A,
∴当AC:AP=AB:AC时,
△ ACP∽△ABC.三、随堂练习1、EE已知,△ABC中,D为AB上一点,画一条过点D的直线(不与AB重合),交AC于E,使所得三角形与原三角形相似,这样的直线最多能画出多少条? 已知,△ABC中,D为AB上一点,画一条过点D的直线(不与AB重合),交另一边于E,使所得三角形与原三角形相似,这样的直线最多能画出多少条?如果将题目变为:EEEEEE四、中考透视1、如图正方形边长是2,BE=CE,MN=1。线段MN的两端在CD、AD上滑动,当DM为多长时,△ABE与以D、M、N为顶点的三角形相似。N 2、已知在△ABC中,∠C=90o ,AC=8cm,BC=6cm,点P从点A出发,沿AC以3厘米/秒的速度向点C移动,点Q从点B出发,沿BA以4厘米/秒的速度向点A移动。
如果P、Q分别从A、B 同时出发,移动时间为t秒 (0
