空间几何体的截面问题-2023届新高考数学高三二轮复习专题讲义(含答案)
文档属性
| 名称 | 空间几何体的截面问题-2023届新高考数学高三二轮复习专题讲义(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 602.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 06:15:00 | ||
图片预览



文档简介
【新高考二轮复习——重难点精选专题】
立体几何-空间几何体的截面问题
专题综述
空间几何体的截面问题在高考考题中是以平面基本性质为命题导向,平行关系为载体,多与空间角交汇,考查变异思维、空间抽象等综合能力.但其抽象性一直是困扰考生的难点,致使很多考生找不到解决问题的突破口.作几何体的截面,需要较强的空间想象能力和动手操作能力,正确判断几何体被一个平面所截的截面形状,关键在于弄清这个平面与几何体的面相交成线的形状和位置,把握截面的定义和方法是解决这类问题的基本途径.
专题探究
探究1:截面的形状
1.作截线与截点的主要根据有:
①确定平面的条件.
②如果两个不重合的平面有一个公共点,那么它们相交于过此点的一条直线.
③如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内.
④根据线面平行的性质定理.
⑤如果两个平面平行,第三个平面和它们相交,那么两条交线平行.
空间几何体的截面作图主要的作法:直接法、平行线法、延长法、辅助平面法;(2021安徽芜湖市单元测试)如图,在正方体
中,点为棱的中点,用平行于体对角线且过点的平面去
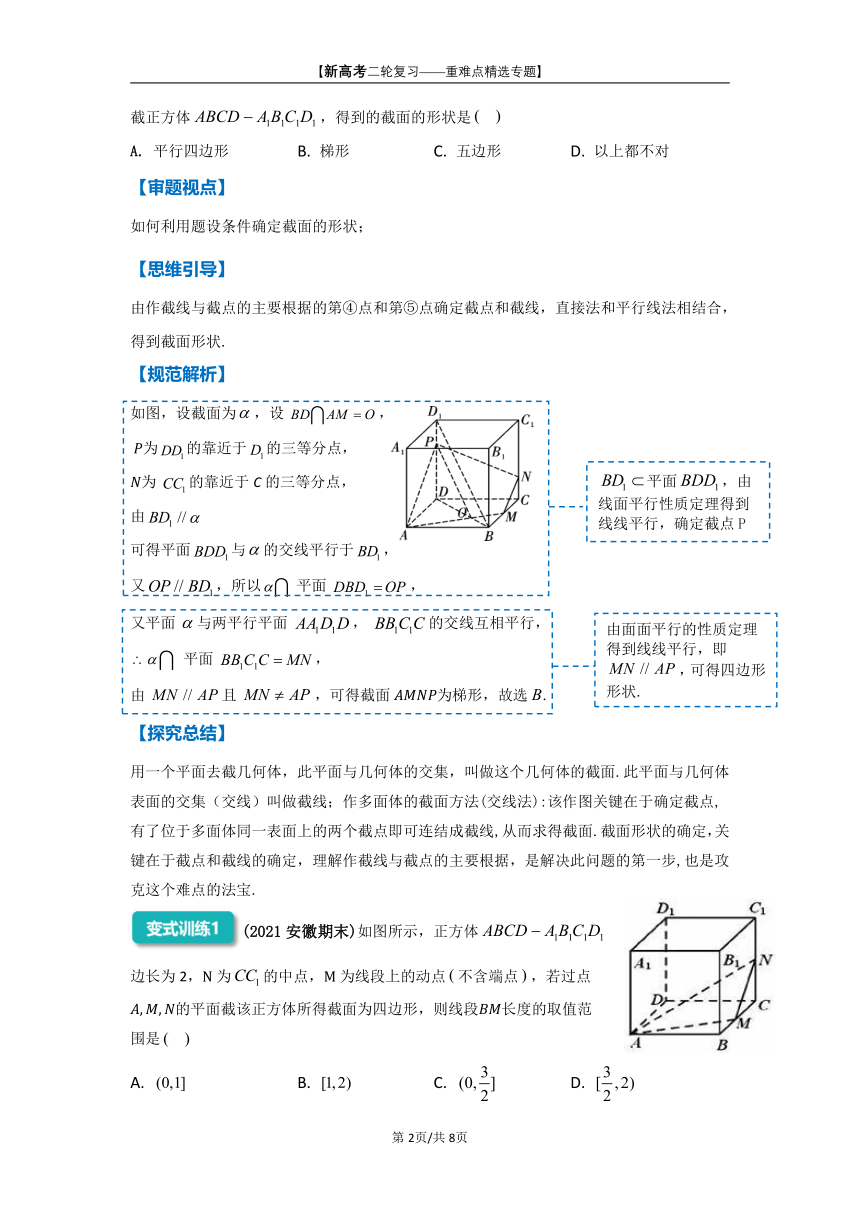
截正方体,得到的截面的形状是
平行四边形 B. 梯形 C. 五边形 D. 以上都不对
【审题视点】
如何利用题设条件确定截面的形状;
【思维引导】
由作截线与截点的主要根据的第④点和第⑤点确定截点和截线,直接法和平行线法相结合,得到截面形状.
【规范解析】
如图,设截面为,设 ,
为的靠近于的三等分点,
为 的靠近于C的三等分点,
由
可得平面与的交线平行于,
又,所以平面 ,
又平面 与两平行平面 , 的交线互相平行,
平面 ,
由 且 ,可得截面 为梯形,故选
【探究总结】
用一个平面去截几何体,此平面与几何体的交集,叫做这个几何体的截面.此平面与几何体表面的交集(交线)叫做截线;作多面体的截面方法(交线法):该作图关键在于确定截点,有了位于多面体同一表面上的两个截点即可连结成截线,从而求得截面.截面形状的确定,关键在于截点和截线的确定,理解作截线与截点的主要根据,是解决此问题的第一步,也是攻克这个难点的法宝.
(2021安徽期末)如图所示,正方体
边长为2,为的中点,为线段上的动点不含端点,若过点
的平面截该正方体所得截面为四边形,则线段长度的取值范
围是
B. C. D.
探究2:截面面积、长度等计算
空间几何体截面的计算要掌握好“定位”“定形”“定量”这三个主要的环节.
第一步,由作截线与截点的主要根据确定截点和截线;
第二步, 根据问题中已知的条件与空间点、线、面的位置关系确定截面的基本特征.
第三步, 运用平面解析几何的有关性质定理与判定定理完成截面相关截面边长、周长、或者面积等数量计算.如果几何体是多面体,其截面是多面形;如果几何体是旋转体,其截面还可能是二次曲线所围成的封闭图形.故平面几何知识是计算正确的基础.
(2021山西月考)棱长为2的正方体中,为棱中点,过点且与平面平行的正方体的截面面积为
A. 5 B. C. D. 6
【审题视点】
计算截面面积,所以要找到截面图形.
【思维引导】
根据正方体的几何特征,平行线法确定与平面平行的正方体的截面,研究截面形状,计算面积;
【规范解析】
取中点,中点,连接、、、、,,如图所示:
棱长为2的正方体中,为棱中点,为棱中点,
为棱中点,
,,
又平面,平面,
过点,且与平面平行的正方体的截面为四边形,
,四边形为菱形,
,,
过点,且与平面平行的正方体的截面面积为 故选
【探究总结】
按照立体几何计算的三步走,难点是确定截点和截线,得到截面的形状,空间问题平面化在这个问题的处理中体现得很明显.
(2021江苏联考)在四面体中,两两垂直且,以为球心,2为半径的球与该四面体每个面的交线的长度和的值为
A. B. C. D.
探究3:截面图形的性质
当条件确定时,截面图形确定,对应几何体的性质很清楚;但当条件变化时,截面形状和位置都是不确定的,此时研究截面的性质必须考虑条件中的所有情况,在选择题中有时可以取特殊位置进行排除得到结果.
(2021山东省枣庄市单元测试) 透明塑料制成的正方体密闭容器的体积为8,注入体积为的液体.如图,将容器下底面的顶点A置于地面上,再将容器倾斜.随着倾斜度的不同,则下列说法正确的是
A. 液面始终与地面平行
B. 时,液面始终呈平行四边形
C. 当时,有液体的部分可呈正三棱锥
D. 当液面与正方体的对角线垂直时,液面面积最大值为
【审题视点】
体积为的液体的液面是什么形状
【思维引导】
根据选项的条件,确定液体的液面的形状,判断选项的正确性.
【规范解析】
解:正方体密闭容器的体积为8,则正方体的边长为2,
由于液面始终是水平面,与地面是平行的,故选项正确;
当时,体积是正方体的一半,如液面正好过棱,
,,,的中点,此时液面是正六边形,
不是平行四边形,故选项B错误;
液面过,的中点时,此时,
液体的部分是正三棱锥,故选项正确;
当液面与正方体的对角线垂直时,液面面积的最大时就是选
项中所列举的正六边形此时液体体积是正方体体积的一半,
则正六边形的边长为,所以面积为,
故选项正确. 故选:
【探究总结】
截面图形的性质研究关键是确定截面的形状,当形状确定时,性质就有了判断的依据;一些常见几何体的特殊位置截面我们应该作为基础知识熟知.
(2021广东省广州市月考)如图,长方体中,,为的中点,过作长方体的截面交棱于N,则
A. 截面可能为六边形
B. 存在点N,使得截面
C. 若截面为平行四边形,则
D. 当N与C重合时,截面面积为
专题升华
在高考立体几何中涉及到空间几何体截面的问题较多, 如: 判断截面的形状、计算出空间几何体的截面周长或面积、或者求与之相关的体积问题、以及最值问题都在考察之列, 但是要顺利地解决这些问题, 都必须首先掌握空间几何体截面的作图。空间几何体截面的探究,要坚持“动手”原则,重视培养“几何画图”的能力,通过对空间位置关系的转化,提高观察力,进而培养学生的直观想象能力,形成和发展数学核心素养.
【答案详解】
变式训练1【答案】
【解析】当时,截面为四边形,
当时,平面AMN与平面也有交线,
故截面为五边形,
平面截正方体所得的截面为四边形时,线段长度的取值范围为
故选
变式训练2【答案】
【解析】因为四面体中,两两垂直且,
由题意知、为等腰直角三角形,以点为球心,为半径作一个球,
设球与的边 分别交于点 ,如图1;
与的边 分别交于点 ,如图2;
易得,则,,
所以,
所以弧 MN的长,同理,弧
在内,如图3,因为,,则,
又如图4,易知弧 是以顶点为圆心,2为半径,圆心角为,则,
所以球面与该四面体每个面的交线的长度和为
故选
变式训练3【答案】
【解析】长方体中,,,M为的中点,过作长方体的截面交棱于N,
设为的中点,根据点N的位置的变化分析可得,
当时,截面为平行四边形,
当时,截面为五边形,
当,即点N与点重合时,截面为梯形,
故选项错误,选项正确;
设截面,因为,所以,
所以只能与C重合才能使,
因为不垂直平面,故此时不成立,故选项B错误;
因为当与重合时,截面为梯形,
如图所示,过M作垂直于于点,
设梯形的高为h,,
则由平面几何知识可得,
解得,,
所以截面的面积为
故选项D正确.故选
立体几何-空间几何体的截面问题
专题综述
空间几何体的截面问题在高考考题中是以平面基本性质为命题导向,平行关系为载体,多与空间角交汇,考查变异思维、空间抽象等综合能力.但其抽象性一直是困扰考生的难点,致使很多考生找不到解决问题的突破口.作几何体的截面,需要较强的空间想象能力和动手操作能力,正确判断几何体被一个平面所截的截面形状,关键在于弄清这个平面与几何体的面相交成线的形状和位置,把握截面的定义和方法是解决这类问题的基本途径.
专题探究
探究1:截面的形状
1.作截线与截点的主要根据有:
①确定平面的条件.
②如果两个不重合的平面有一个公共点,那么它们相交于过此点的一条直线.
③如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内.
④根据线面平行的性质定理.
⑤如果两个平面平行,第三个平面和它们相交,那么两条交线平行.
空间几何体的截面作图主要的作法:直接法、平行线法、延长法、辅助平面法;(2021安徽芜湖市单元测试)如图,在正方体
中,点为棱的中点,用平行于体对角线且过点的平面去
截正方体,得到的截面的形状是
平行四边形 B. 梯形 C. 五边形 D. 以上都不对
【审题视点】
如何利用题设条件确定截面的形状;
【思维引导】
由作截线与截点的主要根据的第④点和第⑤点确定截点和截线,直接法和平行线法相结合,得到截面形状.
【规范解析】
如图,设截面为,设 ,
为的靠近于的三等分点,
为 的靠近于C的三等分点,
由
可得平面与的交线平行于,
又,所以平面 ,
又平面 与两平行平面 , 的交线互相平行,
平面 ,
由 且 ,可得截面 为梯形,故选
【探究总结】
用一个平面去截几何体,此平面与几何体的交集,叫做这个几何体的截面.此平面与几何体表面的交集(交线)叫做截线;作多面体的截面方法(交线法):该作图关键在于确定截点,有了位于多面体同一表面上的两个截点即可连结成截线,从而求得截面.截面形状的确定,关键在于截点和截线的确定,理解作截线与截点的主要根据,是解决此问题的第一步,也是攻克这个难点的法宝.
(2021安徽期末)如图所示,正方体
边长为2,为的中点,为线段上的动点不含端点,若过点
的平面截该正方体所得截面为四边形,则线段长度的取值范
围是
B. C. D.
探究2:截面面积、长度等计算
空间几何体截面的计算要掌握好“定位”“定形”“定量”这三个主要的环节.
第一步,由作截线与截点的主要根据确定截点和截线;
第二步, 根据问题中已知的条件与空间点、线、面的位置关系确定截面的基本特征.
第三步, 运用平面解析几何的有关性质定理与判定定理完成截面相关截面边长、周长、或者面积等数量计算.如果几何体是多面体,其截面是多面形;如果几何体是旋转体,其截面还可能是二次曲线所围成的封闭图形.故平面几何知识是计算正确的基础.
(2021山西月考)棱长为2的正方体中,为棱中点,过点且与平面平行的正方体的截面面积为
A. 5 B. C. D. 6
【审题视点】
计算截面面积,所以要找到截面图形.
【思维引导】
根据正方体的几何特征,平行线法确定与平面平行的正方体的截面,研究截面形状,计算面积;
【规范解析】
取中点,中点,连接、、、、,,如图所示:
棱长为2的正方体中,为棱中点,为棱中点,
为棱中点,
,,
又平面,平面,
过点,且与平面平行的正方体的截面为四边形,
,四边形为菱形,
,,
过点,且与平面平行的正方体的截面面积为 故选
【探究总结】
按照立体几何计算的三步走,难点是确定截点和截线,得到截面的形状,空间问题平面化在这个问题的处理中体现得很明显.
(2021江苏联考)在四面体中,两两垂直且,以为球心,2为半径的球与该四面体每个面的交线的长度和的值为
A. B. C. D.
探究3:截面图形的性质
当条件确定时,截面图形确定,对应几何体的性质很清楚;但当条件变化时,截面形状和位置都是不确定的,此时研究截面的性质必须考虑条件中的所有情况,在选择题中有时可以取特殊位置进行排除得到结果.
(2021山东省枣庄市单元测试) 透明塑料制成的正方体密闭容器的体积为8,注入体积为的液体.如图,将容器下底面的顶点A置于地面上,再将容器倾斜.随着倾斜度的不同,则下列说法正确的是
A. 液面始终与地面平行
B. 时,液面始终呈平行四边形
C. 当时,有液体的部分可呈正三棱锥
D. 当液面与正方体的对角线垂直时,液面面积最大值为
【审题视点】
体积为的液体的液面是什么形状
【思维引导】
根据选项的条件,确定液体的液面的形状,判断选项的正确性.
【规范解析】
解:正方体密闭容器的体积为8,则正方体的边长为2,
由于液面始终是水平面,与地面是平行的,故选项正确;
当时,体积是正方体的一半,如液面正好过棱,
,,,的中点,此时液面是正六边形,
不是平行四边形,故选项B错误;
液面过,的中点时,此时,
液体的部分是正三棱锥,故选项正确;
当液面与正方体的对角线垂直时,液面面积的最大时就是选
项中所列举的正六边形此时液体体积是正方体体积的一半,
则正六边形的边长为,所以面积为,
故选项正确. 故选:
【探究总结】
截面图形的性质研究关键是确定截面的形状,当形状确定时,性质就有了判断的依据;一些常见几何体的特殊位置截面我们应该作为基础知识熟知.
(2021广东省广州市月考)如图,长方体中,,为的中点,过作长方体的截面交棱于N,则
A. 截面可能为六边形
B. 存在点N,使得截面
C. 若截面为平行四边形,则
D. 当N与C重合时,截面面积为
专题升华
在高考立体几何中涉及到空间几何体截面的问题较多, 如: 判断截面的形状、计算出空间几何体的截面周长或面积、或者求与之相关的体积问题、以及最值问题都在考察之列, 但是要顺利地解决这些问题, 都必须首先掌握空间几何体截面的作图。空间几何体截面的探究,要坚持“动手”原则,重视培养“几何画图”的能力,通过对空间位置关系的转化,提高观察力,进而培养学生的直观想象能力,形成和发展数学核心素养.
【答案详解】
变式训练1【答案】
【解析】当时,截面为四边形,
当时,平面AMN与平面也有交线,
故截面为五边形,
平面截正方体所得的截面为四边形时,线段长度的取值范围为
故选
变式训练2【答案】
【解析】因为四面体中,两两垂直且,
由题意知、为等腰直角三角形,以点为球心,为半径作一个球,
设球与的边 分别交于点 ,如图1;
与的边 分别交于点 ,如图2;
易得,则,,
所以,
所以弧 MN的长,同理,弧
在内,如图3,因为,,则,
又如图4,易知弧 是以顶点为圆心,2为半径,圆心角为,则,
所以球面与该四面体每个面的交线的长度和为
故选
变式训练3【答案】
【解析】长方体中,,,M为的中点,过作长方体的截面交棱于N,
设为的中点,根据点N的位置的变化分析可得,
当时,截面为平行四边形,
当时,截面为五边形,
当,即点N与点重合时,截面为梯形,
故选项错误,选项正确;
设截面,因为,所以,
所以只能与C重合才能使,
因为不垂直平面,故此时不成立,故选项B错误;
因为当与重合时,截面为梯形,
如图所示,过M作垂直于于点,
设梯形的高为h,,
则由平面几何知识可得,
解得,,
所以截面的面积为
故选项D正确.故选
同课章节目录
