1.1 锐角三角函数(第一课时)精品课件(共21张PPT)
文档属性
| 名称 | 1.1 锐角三角函数(第一课时)精品课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 16:45:01 | ||
图片预览







文档简介
(共21张PPT)
九下数学同步精品课件
北师大版九年级下册
数学(北师大版)
九年级 下册
1.1 锐角三角函数(第一课时)
第一章 直角三角形的边角关系
2022-2023北师大版九下数学精品课件
课前导入
学习目标
1)经历探索直角三角形中的边角关系的过程,理解正切的含义。
2)根据直角三角形中的边角关系,利用正切解决实际生活问题。
重点
理解正切的含义。
难点
利用正切解决实际生活问题。
情景导入
衡量山“险”与“不险”的标准是什么呢?
山的陡峭程度
探索与思考
观察梯子、地面与墙,你发现了什么?
铅直高度
水平距离
梯子、地面与墙之间形成一个直角三角形,梯子的铅直高度及梯子的水平距离可以看作是它的直角边,梯子的长可以看作是斜边。通常可以从梯子与地面的夹角(倾斜角)考虑梯子的陡峭程度。
探索与思考
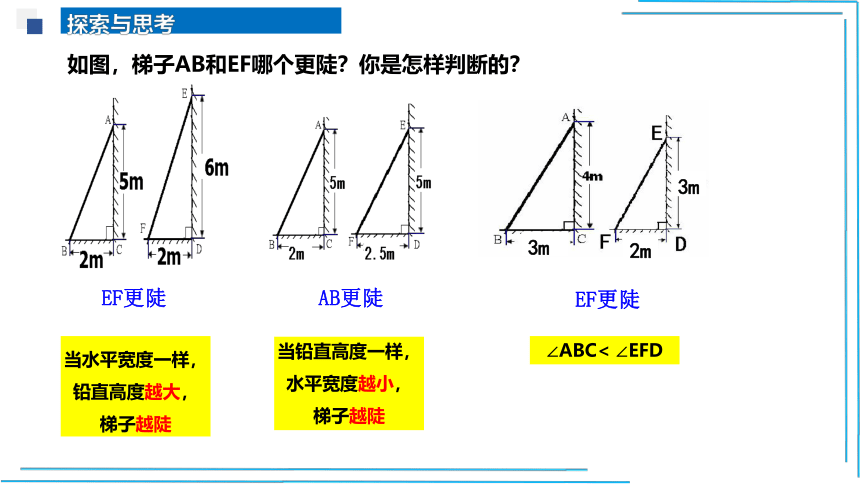
如图,梯子AB和EF哪个更陡?你是怎样判断的?
EF更陡
AB更陡
当铅直高度一样,
水平宽度越小,
梯子越陡
当水平宽度一样,铅直高度越大,梯子越陡
3m
3m
2m
EF更陡
∠ABC< ∠EFD
探索与思考
如图,小明想通过测量B1C1及AC1 ,算出它们的比,来说明梯子AB1的倾斜程度;小亮认为,通过测量B2C2及AC2 ,算出它们的比,也能说明梯子AB1的倾斜程度.你同意谁的看法吗
A
B1
C1
C2
B2
【验证】∵∠A=∠A,∠AC1B1=∠AC2B2=90°,
∴Rt△AC1B1∽Rt△AC2B2
则两人的说法都正确。
【提问】改变B2的位置,刚才的猜测是否成立?
在直角三角形中,当锐角 A 的度数一定时,
不管三角形的大小如何,它的对边与邻边的比是一个固定值.
【注意事项】
1)初中阶段,正切是在直角三角形中定义的, ∠A是一个锐角.
2)tanA是一个完整的符号,它表示∠A的正切.
但∠BAC的正切表示为:tan∠BAC,∠1的正切表示为:tan∠1.
3)tanA﹥0 且没有单位,它表示一个比值.
4)tanA不表示“tan”乘以“A ”.
5)tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.
正切的概念
在 Rt△ABC 中,∠C=90°,我们把锐角A的对边与邻边的比叫做∠A的正切,记作tanA。
即 tan A= =
对边
A
B
C
c
a
b
斜边
邻边
探索与思考
C2
A
B1
C1
B2
B
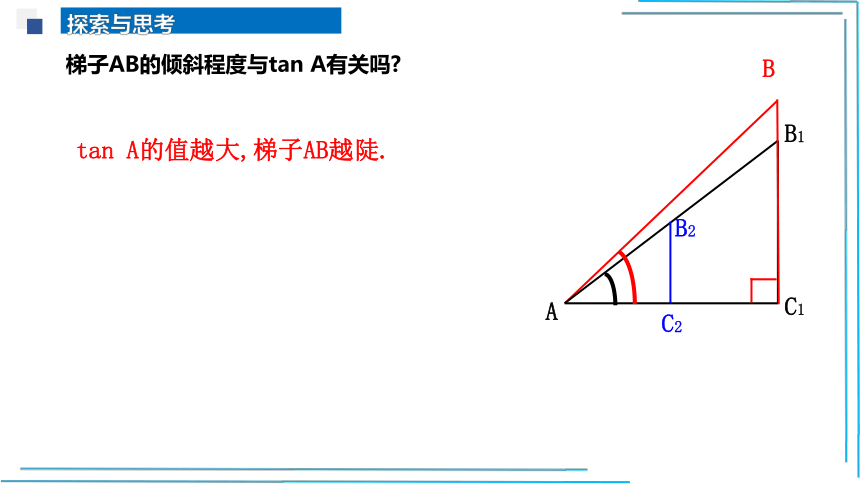
梯子AB的倾斜程度与tan A有关吗
tan A的值越大,梯子AB越陡.
随堂测试
例1 下图表示两个自动扶梯,哪一个自动扶梯比较陡
5m
┌
13m
β
乙
甲
α
4m
┐
8m
解 : 甲梯中,tanα=
乙梯中,tanβ=
∵tanα>tanβ,
∴甲梯更陡.
随堂测试
坡度是地表单元陡缓的程度,通常把坡面的垂直高度h和水平距离l的比叫做坡度(或叫做坡比)用字母i表示。【即坡角的正切值(可写作:i=tan坡角)】
例2 有一山坡在水平方向上每前进100m就升高60m,那么山坡的坡度(即tanα)就是:
100m
60m
┌
α
概念理解
以下对坡度的描述正确的是( )
A.坡度是指倾斜角的度数
B.坡度是指斜坡的铅直高度与水平宽度的比
C.坡度是指斜坡的水平宽度与铅直高度的比
D.坡度是指斜坡的高度与斜坡长度的比
2 (2020·河北唐山市·九年级期末)如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的倾斜角是∠BAC,若,则此斜坡的水平距离AC为( )
A.75m B.50m C.30m D.12m
课堂测试
1 在Rt△ABC中,∠C=90°,AC=1,BC=3,则∠A的正切值为_________
【详解】∵在Rt△ABC中,∠C=90°,AC=1,BC=3,∴∠A的正切值为=3
【详解】
解:因为,又BC=30,所以,,解得:AC=75m,所以,故选A.
课堂测试
3 如图,在6×6的正方形网格中,△ABC的顶点都在小正方形的顶点上,则tan∠BAC的值是( )
A. B. C. D.
【详解】
如图,过点B作BD⊥AC,交AC延长线于点D,
则tan∠BAC==,
故选C.
课堂测试
4 如图,点A(t,3)在第一象限,OA与x轴所夹的锐角为α,tanα= ,则t的值是________.
【详解】
∵点A(t,3)在第一象限,∴AB=3,OB=t,
又∵tanα==,∴t=2.故答案为2.
课堂测试
5 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D,则tan∠BCD= .
6 如图,某人从山脚下的点A走了 200 m后到达山顶的点B,已知点B到山脚的 垂直距离为55 m,求山的坡度(结果精确到0.001).
B
解:由勾股定理可知,
AC= = ≈192.289(m),
∴tan ∠BAC= ≈ ≈0.286.
所以,山的坡度大约是0.286.
课堂测试
7 已知:如图,中,于点,若,,求.
【详解】
解:∵ ∴CD=4
∵ ∴ ∴AD=BD=6
∴tanC =
解题技巧
直角三角形中求锐角正切值的方法:
1)若已知两直角边,直接利用正切的定义求解;
2)若已知一直角边及斜边,另一直角边未知,可先利用勾股定理求出未知的直角边,再利用正切的定义求解。
3)比值与三角形的大小无关,只与倾斜角的大小有关。
课后回顾
正切的概念?
01
课后回顾
坡度和坡度角的概念?
02
直角三角形中求正切值的方法?
03
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
九下数学同步精品课件
北师大版九年级下册
数学(北师大版)
九年级 下册
1.1 锐角三角函数(第一课时)
第一章 直角三角形的边角关系
2022-2023北师大版九下数学精品课件
课前导入
学习目标
1)经历探索直角三角形中的边角关系的过程,理解正切的含义。
2)根据直角三角形中的边角关系,利用正切解决实际生活问题。
重点
理解正切的含义。
难点
利用正切解决实际生活问题。
情景导入
衡量山“险”与“不险”的标准是什么呢?
山的陡峭程度
探索与思考
观察梯子、地面与墙,你发现了什么?
铅直高度
水平距离
梯子、地面与墙之间形成一个直角三角形,梯子的铅直高度及梯子的水平距离可以看作是它的直角边,梯子的长可以看作是斜边。通常可以从梯子与地面的夹角(倾斜角)考虑梯子的陡峭程度。
探索与思考
如图,梯子AB和EF哪个更陡?你是怎样判断的?
EF更陡
AB更陡
当铅直高度一样,
水平宽度越小,
梯子越陡
当水平宽度一样,铅直高度越大,梯子越陡
3m
3m
2m
EF更陡
∠ABC< ∠EFD
探索与思考
如图,小明想通过测量B1C1及AC1 ,算出它们的比,来说明梯子AB1的倾斜程度;小亮认为,通过测量B2C2及AC2 ,算出它们的比,也能说明梯子AB1的倾斜程度.你同意谁的看法吗
A
B1
C1
C2
B2
【验证】∵∠A=∠A,∠AC1B1=∠AC2B2=90°,
∴Rt△AC1B1∽Rt△AC2B2
则两人的说法都正确。
【提问】改变B2的位置,刚才的猜测是否成立?
在直角三角形中,当锐角 A 的度数一定时,
不管三角形的大小如何,它的对边与邻边的比是一个固定值.
【注意事项】
1)初中阶段,正切是在直角三角形中定义的, ∠A是一个锐角.
2)tanA是一个完整的符号,它表示∠A的正切.
但∠BAC的正切表示为:tan∠BAC,∠1的正切表示为:tan∠1.
3)tanA﹥0 且没有单位,它表示一个比值.
4)tanA不表示“tan”乘以“A ”.
5)tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.
正切的概念
在 Rt△ABC 中,∠C=90°,我们把锐角A的对边与邻边的比叫做∠A的正切,记作tanA。
即 tan A= =
对边
A
B
C
c
a
b
斜边
邻边
探索与思考
C2
A
B1
C1
B2
B
梯子AB的倾斜程度与tan A有关吗
tan A的值越大,梯子AB越陡.
随堂测试
例1 下图表示两个自动扶梯,哪一个自动扶梯比较陡
5m
┌
13m
β
乙
甲
α
4m
┐
8m
解 : 甲梯中,tanα=
乙梯中,tanβ=
∵tanα>tanβ,
∴甲梯更陡.
随堂测试
坡度是地表单元陡缓的程度,通常把坡面的垂直高度h和水平距离l的比叫做坡度(或叫做坡比)用字母i表示。【即坡角的正切值(可写作:i=tan坡角)】
例2 有一山坡在水平方向上每前进100m就升高60m,那么山坡的坡度(即tanα)就是:
100m
60m
┌
α
概念理解
以下对坡度的描述正确的是( )
A.坡度是指倾斜角的度数
B.坡度是指斜坡的铅直高度与水平宽度的比
C.坡度是指斜坡的水平宽度与铅直高度的比
D.坡度是指斜坡的高度与斜坡长度的比
2 (2020·河北唐山市·九年级期末)如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的倾斜角是∠BAC,若,则此斜坡的水平距离AC为( )
A.75m B.50m C.30m D.12m
课堂测试
1 在Rt△ABC中,∠C=90°,AC=1,BC=3,则∠A的正切值为_________
【详解】∵在Rt△ABC中,∠C=90°,AC=1,BC=3,∴∠A的正切值为=3
【详解】
解:因为,又BC=30,所以,,解得:AC=75m,所以,故选A.
课堂测试
3 如图,在6×6的正方形网格中,△ABC的顶点都在小正方形的顶点上,则tan∠BAC的值是( )
A. B. C. D.
【详解】
如图,过点B作BD⊥AC,交AC延长线于点D,
则tan∠BAC==,
故选C.
课堂测试
4 如图,点A(t,3)在第一象限,OA与x轴所夹的锐角为α,tanα= ,则t的值是________.
【详解】
∵点A(t,3)在第一象限,∴AB=3,OB=t,
又∵tanα==,∴t=2.故答案为2.
课堂测试
5 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D,则tan∠BCD= .
6 如图,某人从山脚下的点A走了 200 m后到达山顶的点B,已知点B到山脚的 垂直距离为55 m,求山的坡度(结果精确到0.001).
B
解:由勾股定理可知,
AC= = ≈192.289(m),
∴tan ∠BAC= ≈ ≈0.286.
所以,山的坡度大约是0.286.
课堂测试
7 已知:如图,中,于点,若,,求.
【详解】
解:∵ ∴CD=4
∵ ∴ ∴AD=BD=6
∴tanC =
解题技巧
直角三角形中求锐角正切值的方法:
1)若已知两直角边,直接利用正切的定义求解;
2)若已知一直角边及斜边,另一直角边未知,可先利用勾股定理求出未知的直角边,再利用正切的定义求解。
3)比值与三角形的大小无关,只与倾斜角的大小有关。
课后回顾
正切的概念?
01
课后回顾
坡度和坡度角的概念?
02
直角三角形中求正切值的方法?
03
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
