1.1 锐角三角形(第二课时)精品课件(19张PPT)
文档属性
| 名称 | 1.1 锐角三角形(第二课时)精品课件(19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
九下数学同步精品课件
北师大版九年级下册
数学(北师大版)
九年级 下册
1.1 锐角三角函数(第二课时)
第一章 直角三角形的边角关系
2022-2023北师大版九下数学精品课件
课前导入
学习目标
1)经历探索直角三角形中边角关系的过程,理解正弦和余弦的含义。
2)能够运用sinA、cosA表示直角三角形的边角关系。
3)根据直角三角形中的边角关系,进行简单计算。
重点
理解正弦和余弦的含义。
难点
根据直角三角形中的边角关系,进行简单计算。
探索与思考
【探索】任意画Rt△ABC和Rt△A’B’C‘,使∠C=∠C’=90°,∠A=∠A‘,那么与’有什么关系,你能解释一下吗?
∵ ∠C=∠C'=90°,∠A=∠A'∴ Rt△ABC∽Rt△A'B'C’∴ = ∴ =
在直角三角形中,当锐角 A 的度数一定时,
不管三角形的大小如何,它的对边与斜边的比是一个固定值.
在Rt△ABC中,∠C=90°,当锐角A确定时,∠A的对边与邻边的比就随之确定,此时其他边之间的比是否也随之确定呢?
正弦
在 Rt△ABC 中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的正弦,记作:sinA.
对边
A
B
C
c
a
b
斜边
即 sin A= =
正弦的表示:
1)sinA 、 sin40 ° 、 sinα(省去角的符号)
2)sin∠ABC、 sin∠1 (不能省去角的符号)
探索与思考
在Rt△ABC中,∠C=90°,当锐角A确定时,∠A的对边与邻边的比就随之确定,此时其他边之间的比是否也随之确定呢?
【探索】任意画Rt△ABC和Rt△A‘B’C‘,使∠C=∠C’=90°,∠A=∠A‘,那么 与 有什么关系.你能解释一下吗?
∵ ∠C=∠C’=90°,∠A=∠A’∴ Rt△ABC∽Rt△A’B’C’∴ = ∴ =
在直角三角形中,当锐角 A 的度数一定时,
不管三角形的大小如何,它的邻边与斜边的比是一个固定值.
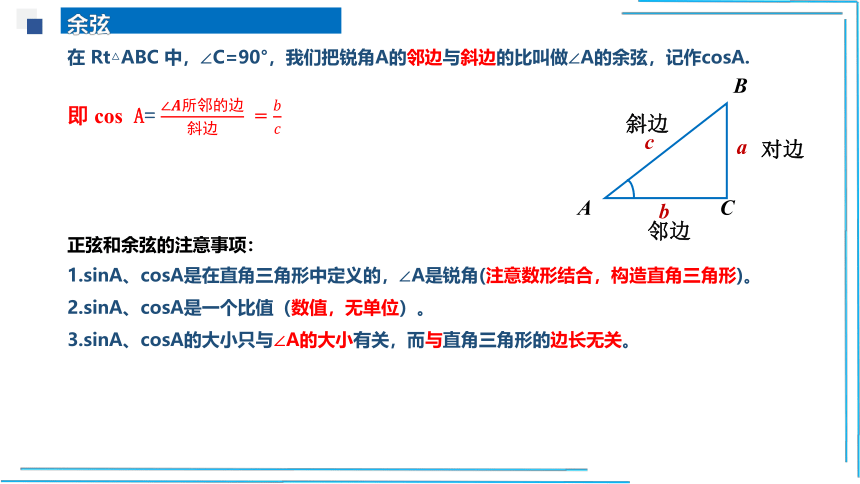
余弦
在 Rt△ABC 中,∠C=90°,我们把锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA.
即 cos A= =
对边
A
B
C
c
a
b
斜边
邻边
正弦和余弦的注意事项:
1.sinA、cosA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。
2.sinA、cosA是一个比值(数值,无单位)。
3.sinA、cosA的大小只与∠A的大小有关,而与直角三角形的边长无关。
锐角三角函数
对于锐角A的每一个确定的值,sinA、cosA、tanA都有唯一的确定的值与它对应,所以把锐角A的正弦、余弦、正切叫做∠A的锐角三角函数。
探索与思考
我们知道,梯子的倾斜程度与tanA有关系,tanA越大,梯子越陡,那么梯子的倾斜程度与sinA和cosA有关系吗?是怎样的关系?
铅直高度
A
B
C
梯子长
水平距离
∵ sin A= 而梯子长度的固定值,
∴sin A 越大,铅直高度越大,梯子越陡。
∵ cos A= 而梯子长度的固定值,
∴cos A 越小,水平距离越小,梯子越陡。
1)梯子的倾斜程度与sinA和cosA有关;
2)sinA越大,梯子越陡;cosA越小,梯子越陡。
课堂基础练
如图,在Rt△ABC , ∠B=900 , AC=20 , sinA=0.6 ,求BC的长.
20
A
C
B
┌
解: 在Rt△ABC中,
课堂基础练
在 Rt△ABC 中,∠C=90°,若AB=10,BC=6,求tanA,sinA,cosA的值
由勾股定理得AC= =8
因此sinA= = cosA= = tanA= =
A
B
C
10
6
课堂基础练
如图(1)(2),在Rt△ABC中,∠C=90°,求sinA和cosA、sinB和cosB的值,观察结果,你发现了什么?
1)解:如图(1),
在 Rt△ABC 中,由勾股定理得AB= =5
sin A= = ,sin B= =
cos A= = ,cos B= =
2)解:如图(2),
在 Rt△ABC 中,由勾股定理得AC= =12
sin A= = ,sin B= =
cos A= =,cos B= =
在Rt△ABC(∠C=90°)中,sin A=cos B
随堂测试
如图,在平面直角坐标系中,点A的坐标为(3,4),那么sinα的值是( )
A. B. C. D.
【详解】作AB⊥x轴交x轴于点B,
∵A(3,4),∴AB=4,BO=3,∴AO===5,
∴sin ==.故选C.
B
把△ABC三边的长度都扩大为原来的2倍,则锐角A的正弦函数值()
A.不变 B.缩小为原来的 C.扩大为原来的2倍 D.不能确定
【详解】因为△ABC三边的长度都扩大为原来的2倍所得的三角形与原三角形相似,
所以锐角A的大小没改变,则锐角A的正弦函数值也不变。故选A。
随堂测试
在 Rt△ABC 中,∠C=90°,若∠A=30°且 BC=2,求cosA=
∵ ∠C=90°,∠A=30°, BC=2∴ AB=4,
由勾股定理得AC= =2∴cos A=
在 Rt△ABC 中,∠C=90°,若∠A=45°且 BC=2,求cosA=
∵ ∠C=90°,∠A=45°∴ BC=AC=2
由勾股定理得AB= =2∴cos A=
Rt△ABC中,∠C=90°,cosA=,AC=6cm,那么BC等于_____.
在中,∵,,
则.
A
B
C
随堂测试
如图,已知Rt△ABC中,斜边BC上的高AD=4,cosB=,则AC=____.
【详解】
∵△ABC是直角三角形,AD是斜边BC上的高
∴∠BAC=∠ADB=90°
∵∠B+∠BAD=90°,∠B+∠C=90°,∠CAD+∠C=90°,cosB=
∴∠B=∠CAD,cos∠CAD=
在Rt△ADC中,AD=4,
∴AC==5.
随堂测试-提高
已知在Rt△ABC中,∠C=90°,sinA=,则tanB的值为( )
A. B. C. D.
【详解】
sinA=
设三边分别为BC=3x,AC=4x,AB=5x
tanB=
故选A
课后回顾
正弦的概念?
01
课后回顾
余弦的概念?
02
在Rt△ABC中,sin A和cos B之间的关系?
03
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
九下数学同步精品课件
北师大版九年级下册
数学(北师大版)
九年级 下册
1.1 锐角三角函数(第二课时)
第一章 直角三角形的边角关系
2022-2023北师大版九下数学精品课件
课前导入
学习目标
1)经历探索直角三角形中边角关系的过程,理解正弦和余弦的含义。
2)能够运用sinA、cosA表示直角三角形的边角关系。
3)根据直角三角形中的边角关系,进行简单计算。
重点
理解正弦和余弦的含义。
难点
根据直角三角形中的边角关系,进行简单计算。
探索与思考
【探索】任意画Rt△ABC和Rt△A’B’C‘,使∠C=∠C’=90°,∠A=∠A‘,那么与’有什么关系,你能解释一下吗?
∵ ∠C=∠C'=90°,∠A=∠A'∴ Rt△ABC∽Rt△A'B'C’∴ = ∴ =
在直角三角形中,当锐角 A 的度数一定时,
不管三角形的大小如何,它的对边与斜边的比是一个固定值.
在Rt△ABC中,∠C=90°,当锐角A确定时,∠A的对边与邻边的比就随之确定,此时其他边之间的比是否也随之确定呢?
正弦
在 Rt△ABC 中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的正弦,记作:sinA.
对边
A
B
C
c
a
b
斜边
即 sin A= =
正弦的表示:
1)sinA 、 sin40 ° 、 sinα(省去角的符号)
2)sin∠ABC、 sin∠1 (不能省去角的符号)
探索与思考
在Rt△ABC中,∠C=90°,当锐角A确定时,∠A的对边与邻边的比就随之确定,此时其他边之间的比是否也随之确定呢?
【探索】任意画Rt△ABC和Rt△A‘B’C‘,使∠C=∠C’=90°,∠A=∠A‘,那么 与 有什么关系.你能解释一下吗?
∵ ∠C=∠C’=90°,∠A=∠A’∴ Rt△ABC∽Rt△A’B’C’∴ = ∴ =
在直角三角形中,当锐角 A 的度数一定时,
不管三角形的大小如何,它的邻边与斜边的比是一个固定值.
余弦
在 Rt△ABC 中,∠C=90°,我们把锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA.
即 cos A= =
对边
A
B
C
c
a
b
斜边
邻边
正弦和余弦的注意事项:
1.sinA、cosA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。
2.sinA、cosA是一个比值(数值,无单位)。
3.sinA、cosA的大小只与∠A的大小有关,而与直角三角形的边长无关。
锐角三角函数
对于锐角A的每一个确定的值,sinA、cosA、tanA都有唯一的确定的值与它对应,所以把锐角A的正弦、余弦、正切叫做∠A的锐角三角函数。
探索与思考
我们知道,梯子的倾斜程度与tanA有关系,tanA越大,梯子越陡,那么梯子的倾斜程度与sinA和cosA有关系吗?是怎样的关系?
铅直高度
A
B
C
梯子长
水平距离
∵ sin A= 而梯子长度的固定值,
∴sin A 越大,铅直高度越大,梯子越陡。
∵ cos A= 而梯子长度的固定值,
∴cos A 越小,水平距离越小,梯子越陡。
1)梯子的倾斜程度与sinA和cosA有关;
2)sinA越大,梯子越陡;cosA越小,梯子越陡。
课堂基础练
如图,在Rt△ABC , ∠B=900 , AC=20 , sinA=0.6 ,求BC的长.
20
A
C
B
┌
解: 在Rt△ABC中,
课堂基础练
在 Rt△ABC 中,∠C=90°,若AB=10,BC=6,求tanA,sinA,cosA的值
由勾股定理得AC= =8
因此sinA= = cosA= = tanA= =
A
B
C
10
6
课堂基础练
如图(1)(2),在Rt△ABC中,∠C=90°,求sinA和cosA、sinB和cosB的值,观察结果,你发现了什么?
1)解:如图(1),
在 Rt△ABC 中,由勾股定理得AB= =5
sin A= = ,sin B= =
cos A= = ,cos B= =
2)解:如图(2),
在 Rt△ABC 中,由勾股定理得AC= =12
sin A= = ,sin B= =
cos A= =,cos B= =
在Rt△ABC(∠C=90°)中,sin A=cos B
随堂测试
如图,在平面直角坐标系中,点A的坐标为(3,4),那么sinα的值是( )
A. B. C. D.
【详解】作AB⊥x轴交x轴于点B,
∵A(3,4),∴AB=4,BO=3,∴AO===5,
∴sin ==.故选C.
B
把△ABC三边的长度都扩大为原来的2倍,则锐角A的正弦函数值()
A.不变 B.缩小为原来的 C.扩大为原来的2倍 D.不能确定
【详解】因为△ABC三边的长度都扩大为原来的2倍所得的三角形与原三角形相似,
所以锐角A的大小没改变,则锐角A的正弦函数值也不变。故选A。
随堂测试
在 Rt△ABC 中,∠C=90°,若∠A=30°且 BC=2,求cosA=
∵ ∠C=90°,∠A=30°, BC=2∴ AB=4,
由勾股定理得AC= =2∴cos A=
在 Rt△ABC 中,∠C=90°,若∠A=45°且 BC=2,求cosA=
∵ ∠C=90°,∠A=45°∴ BC=AC=2
由勾股定理得AB= =2∴cos A=
Rt△ABC中,∠C=90°,cosA=,AC=6cm,那么BC等于_____.
在中,∵,,
则.
A
B
C
随堂测试
如图,已知Rt△ABC中,斜边BC上的高AD=4,cosB=,则AC=____.
【详解】
∵△ABC是直角三角形,AD是斜边BC上的高
∴∠BAC=∠ADB=90°
∵∠B+∠BAD=90°,∠B+∠C=90°,∠CAD+∠C=90°,cosB=
∴∠B=∠CAD,cos∠CAD=
在Rt△ADC中,AD=4,
∴AC==5.
随堂测试-提高
已知在Rt△ABC中,∠C=90°,sinA=,则tanB的值为( )
A. B. C. D.
【详解】
sinA=
设三边分别为BC=3x,AC=4x,AB=5x
tanB=
故选A
课后回顾
正弦的概念?
01
课后回顾
余弦的概念?
02
在Rt△ABC中,sin A和cos B之间的关系?
03
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
