相似三角形的应用[下学期]
文档属性
| 名称 | 相似三角形的应用[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 526.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-13 17:28:00 | ||
图片预览



文档简介
课件13张PPT。相似三角形的应用(1)一、情景创设
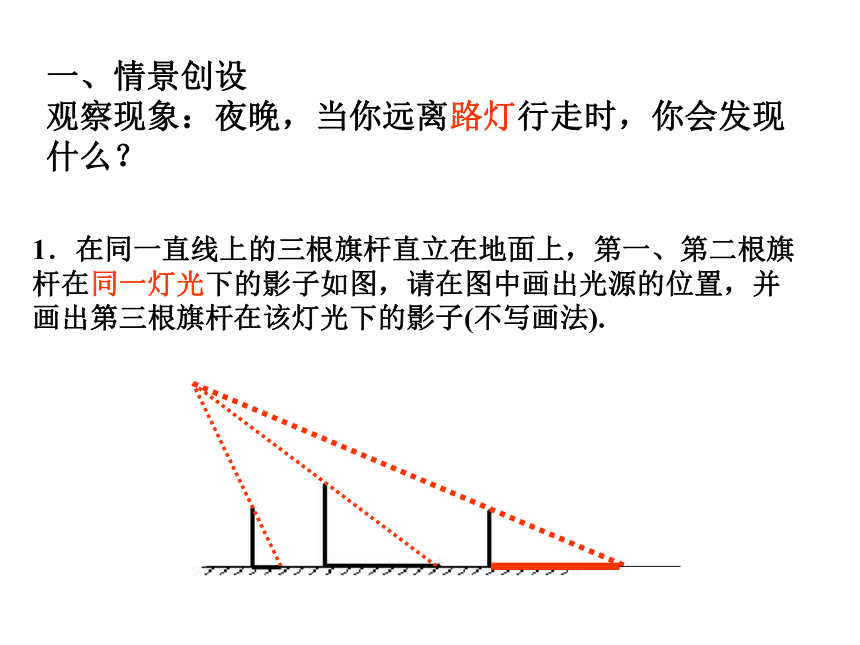
观察现象:夜晚,当你远离路灯行走时,你会发现什么?1.在同一直线上的三根旗杆直立在地面上,第一、第二根旗杆在同一灯光下的影子如图,请在图中画出光源的位置,并画出第三根旗杆在该灯光下的影子(不写画法).
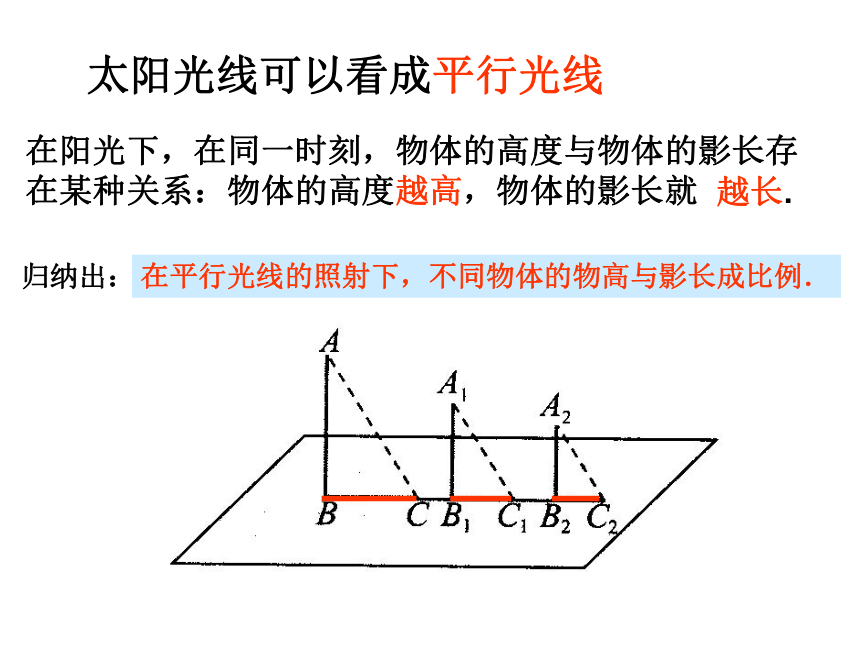
太阳光线可以看成平行光线 在阳光下,在同一时刻,物体的高度与物体的影长存在某种关系:物体的高度越高,物体的影长就越长.归纳出:在平行光线的照射下,不同物体的物高与影长成比例.练习1:在同一时刻物体的高度与它的影长成正比例,在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为60米,那么高楼的高度是多少米?
解:设高楼的高度为X米,则
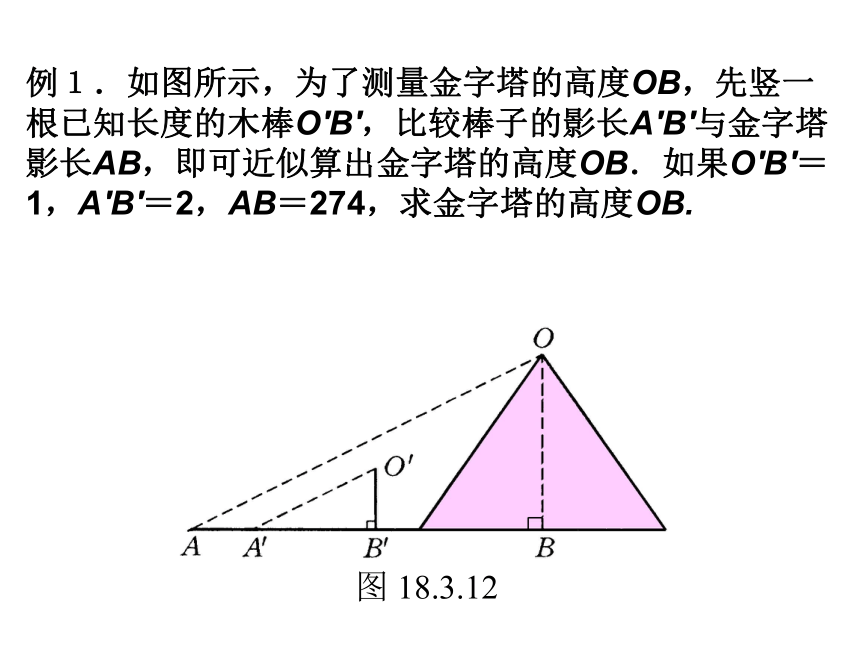
答:楼高36米. 胡夫金字塔是埃及现存规模最大的金字塔,被喻为“世界古代七大奇观之一”。塔的4个斜面正对东南西北四个方向,塔基呈正方形,每边长约230多米。据考证,为建成大金字塔,共动用了10万人花了20年时间.原高146.59米,但由于经过几千年的风吹雨打,顶端被风化吹蚀.所以高度有所降低 。 走近金字塔例1.如图所示,为了测量金字塔的高度OB,先竖一根已知长度的木棒O′B′,比较棒子的影长A′B′与金字塔影长AB,即可近似算出金字塔的高度OB.如果O′B′=1,A′B′=2,AB=274,求金字塔的高度OB.练习 如图,小明在打网球时,使球恰好能打过网,
而且落在离网5米的位置上,求球拍击球的高度h.3.如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB.
D例4.如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在近岸取点Q和S,使点P.Q.S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得 QS=45m,ST=90m,QR=60m,求河的宽度PQ. PSTQRab459060x5.如图,铁道口的栏杆短臂长1m,长臂长16m,当短臂的端点下降0.5m时,长臂端点应升高多少m?116O6.如图,阳光通过窗户照到室内,在地面上留下2.7m宽的亮区,已知亮区一边到窗口下的墙角距离EC=8.7m,窗口高AB=1.8m,那么窗口底边离地面的高BC是多少呢?8.71.82.77,某数学课外实习小组想利用树影测量树高,他们在同一时刻测得一身高为1.5米的同学的影子长为1.35米,因大树靠近一栋建筑物,大树的影子不全在地面上,他们测得地面部分的影子长BC=3.6米,墙上影子高CD=1.8米,求树高AB。
3.61.8E课堂小结:一 、相似三角形的应用主要有如下两个方面
1 测高(不能直接使用皮尺或刻度尺量的)
2 测距(不能直接测量的两点间的距离)、测高的方法
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长的比例”的原理解决 、测距的方法
测量不能到达两点间的距离,常构造相似三角形求解
观察现象:夜晚,当你远离路灯行走时,你会发现什么?1.在同一直线上的三根旗杆直立在地面上,第一、第二根旗杆在同一灯光下的影子如图,请在图中画出光源的位置,并画出第三根旗杆在该灯光下的影子(不写画法).
太阳光线可以看成平行光线 在阳光下,在同一时刻,物体的高度与物体的影长存在某种关系:物体的高度越高,物体的影长就越长.归纳出:在平行光线的照射下,不同物体的物高与影长成比例.练习1:在同一时刻物体的高度与它的影长成正比例,在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为60米,那么高楼的高度是多少米?
解:设高楼的高度为X米,则
答:楼高36米. 胡夫金字塔是埃及现存规模最大的金字塔,被喻为“世界古代七大奇观之一”。塔的4个斜面正对东南西北四个方向,塔基呈正方形,每边长约230多米。据考证,为建成大金字塔,共动用了10万人花了20年时间.原高146.59米,但由于经过几千年的风吹雨打,顶端被风化吹蚀.所以高度有所降低 。 走近金字塔例1.如图所示,为了测量金字塔的高度OB,先竖一根已知长度的木棒O′B′,比较棒子的影长A′B′与金字塔影长AB,即可近似算出金字塔的高度OB.如果O′B′=1,A′B′=2,AB=274,求金字塔的高度OB.练习 如图,小明在打网球时,使球恰好能打过网,
而且落在离网5米的位置上,求球拍击球的高度h.3.如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB.
D例4.如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在近岸取点Q和S,使点P.Q.S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得 QS=45m,ST=90m,QR=60m,求河的宽度PQ. PSTQRab459060x5.如图,铁道口的栏杆短臂长1m,长臂长16m,当短臂的端点下降0.5m时,长臂端点应升高多少m?116O6.如图,阳光通过窗户照到室内,在地面上留下2.7m宽的亮区,已知亮区一边到窗口下的墙角距离EC=8.7m,窗口高AB=1.8m,那么窗口底边离地面的高BC是多少呢?8.71.82.77,某数学课外实习小组想利用树影测量树高,他们在同一时刻测得一身高为1.5米的同学的影子长为1.35米,因大树靠近一栋建筑物,大树的影子不全在地面上,他们测得地面部分的影子长BC=3.6米,墙上影子高CD=1.8米,求树高AB。
3.61.8E课堂小结:一 、相似三角形的应用主要有如下两个方面
1 测高(不能直接使用皮尺或刻度尺量的)
2 测距(不能直接测量的两点间的距离)、测高的方法
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长的比例”的原理解决 、测距的方法
测量不能到达两点间的距离,常构造相似三角形求解
