相似三角形的判定[下学期]
文档属性
| 名称 | 相似三角形的判定[下学期] |
|
|
| 格式 | rar | ||
| 文件大小 | 109.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-14 00:00:00 | ||
图片预览


文档简介
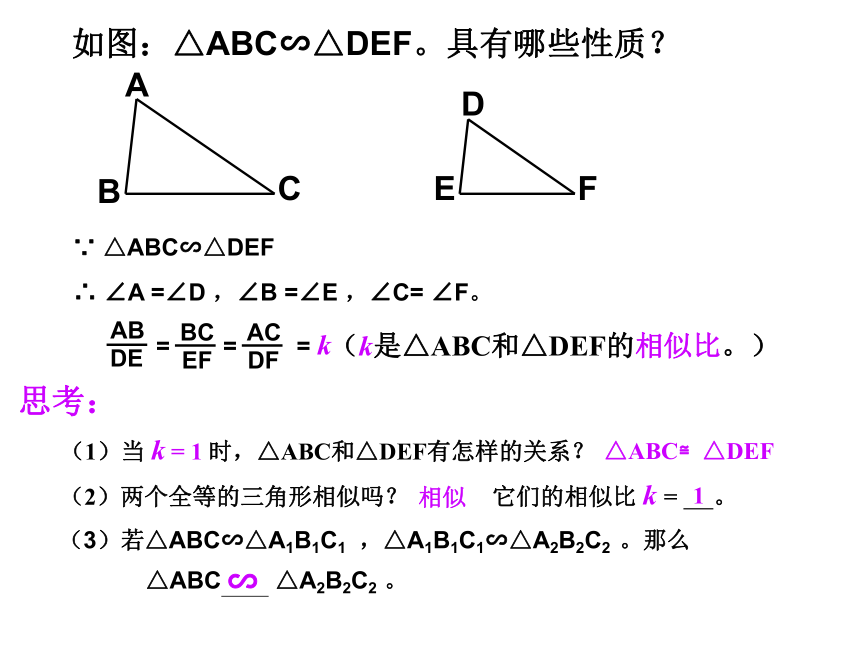
课件15张PPT。相似多边形的性质:对应角相等,对应边的比相等。观察下列图形:∴ ∠A =∠D ,∠B =∠E ,∠C= ∠F。FDBACE∵ △ABC∽△DEF如图:△ABC∽△DEF。具有哪些性质?(k是△ABC和△DEF的相似比。)思考:(1)当 k = 1 时,△ABC和△DEF有怎样的关系?△ABC≌△DEF(2)两个全等的三角形相似吗? 相似它们的相似比 k = 。1(3)若△ABC∽△A1B1C1 ,△A1B1C1∽△A2B2C2 。那么
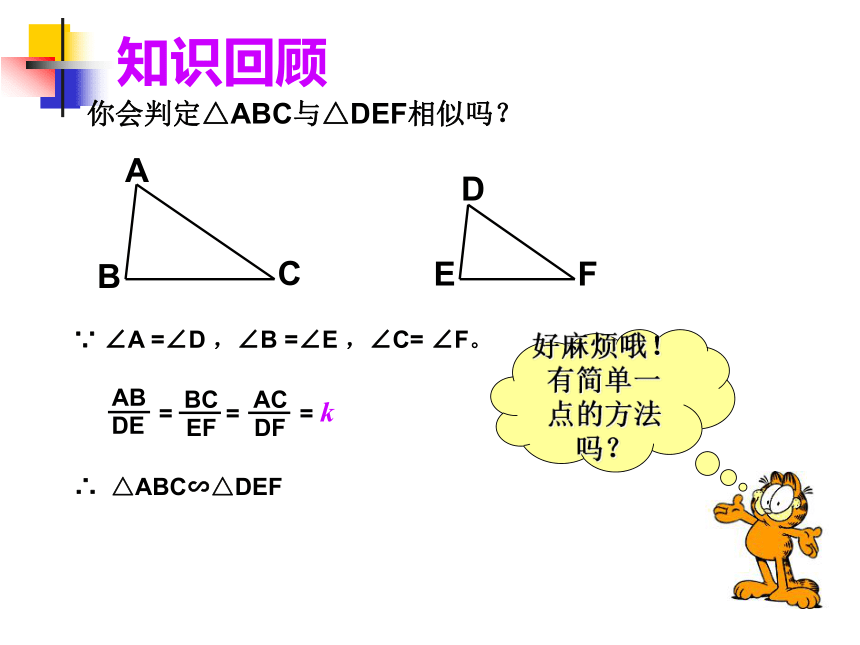
△ABC △A2B2C2 。∽你会判定△ABC与△DEF相似吗?FDBACE知识回顾∵ ∠A =∠D ,∠B =∠E ,∠C= ∠F。∴ △ABC∽△DEF好麻烦哦!
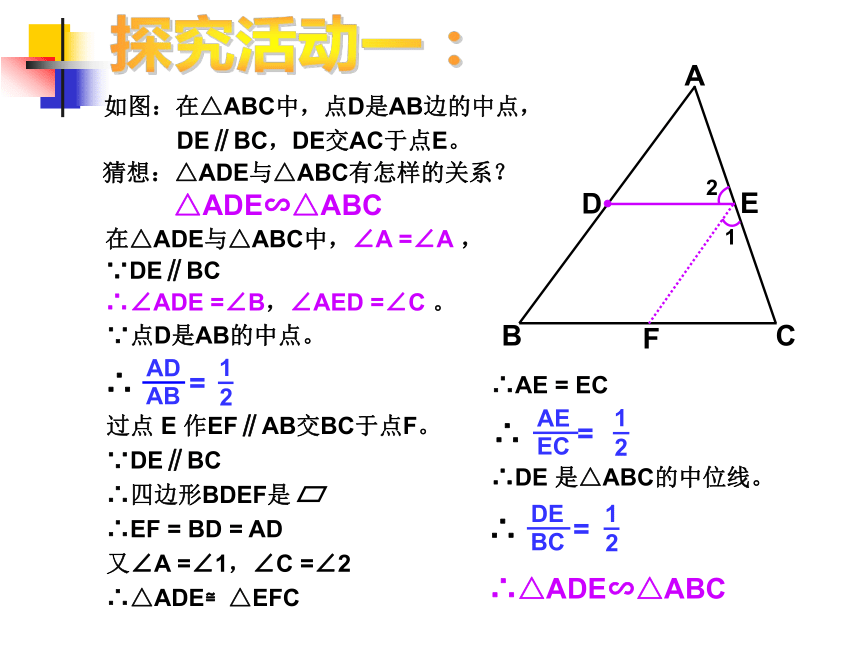
有简单一点的方法吗?相似三角形的判定FDBACE如图:在△ABC中,点D是AB边的中点,
DE∥BC,DE交AC于点E。猜想:△ADE与△ABC有怎样的关系?△ADE∽△ABC在△ADE与△ABC中,∠A =∠A ,
∵DE∥BC
∴∠ADE =∠B,∠AED =∠C 。∵点D是AB的中点。过点 E 作EF∥AB交BC于点F。
∵DE∥BC
∴四边形BDEF是
∴EF = BD = AD
又∠A =∠1,∠C =∠2
∴△ADE≌△EFC∴AE = EC∴△ADE∽△ABC∴DE 是△ABC的中位线。探究活动一: 平行于三角形一边的直线与其他两边相交。所
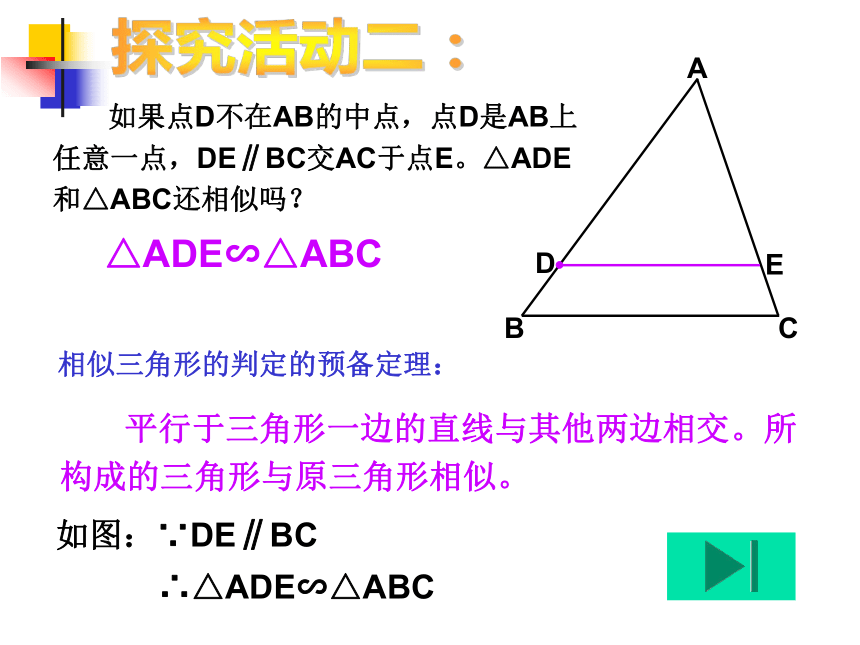
构成的三角形与原三角形相似。如图:∵DE∥BC
∴△ADE∽△ABC 如果点D不在AB的中点,点D是AB上
任意一点,DE∥BC交AC于点E。△ADE
和△ABC还相似吗?△ADE∽△ABC探究活动二:相似三角形的判定的预备定理: 如果点D在AB所在的直线上,继续改变点D的位置。
DE∥BC交AC于点E。△ADE和△ABC还相似吗?∵DE∥BC
∴△ADE∽△ABC∵DE∥BC
∴△ADE∽△ABC探究活动三:考考你的眼力! 如图: ABCD,E是AB延长线上一点。DE与AC和
BC分别相交于点O、F。你能找出图中的相似三角形吗?
并说明理由。∴△BDM∽△BCA应用举例解:∵MD∥AC,又∵ ME∥AB,∴△CEM∽△CAB3份学以致用如图:一条河流,在河流的北岸点A处有一根高压电线杆。河流的南岸点B处有一颗大树。且电线杆在大树的正北方向上。在大树的正东方的点C处有一雕像,你能利用本节课学习的知识大致测算出电线杆A与大树B之间的距离吗? 若用皮尺测得:BC=50米,CD=20米,DE=60米,你能计算出电线杆A与大树B之间的距离吗?ABCDE你学会了什么?∵DE∥BC
∴△ADE∽△ABC1、相似三角形的判定方法:由平行得相似。2、相似三角形性质的应用。谢谢同学们!ABCDEB3B2B1C1C2C3FHMNa4a3aaaaaa2a3、如图:在△ABC中,DE∥BC,
BE与DC相交于点O。OD = 2 cm,
OC = 4 cm,AC = 10 cm。
求:AE的长。
△ABC △A2B2C2 。∽你会判定△ABC与△DEF相似吗?FDBACE知识回顾∵ ∠A =∠D ,∠B =∠E ,∠C= ∠F。∴ △ABC∽△DEF好麻烦哦!
有简单一点的方法吗?相似三角形的判定FDBACE如图:在△ABC中,点D是AB边的中点,
DE∥BC,DE交AC于点E。猜想:△ADE与△ABC有怎样的关系?△ADE∽△ABC在△ADE与△ABC中,∠A =∠A ,
∵DE∥BC
∴∠ADE =∠B,∠AED =∠C 。∵点D是AB的中点。过点 E 作EF∥AB交BC于点F。
∵DE∥BC
∴四边形BDEF是
∴EF = BD = AD
又∠A =∠1,∠C =∠2
∴△ADE≌△EFC∴AE = EC∴△ADE∽△ABC∴DE 是△ABC的中位线。探究活动一: 平行于三角形一边的直线与其他两边相交。所
构成的三角形与原三角形相似。如图:∵DE∥BC
∴△ADE∽△ABC 如果点D不在AB的中点,点D是AB上
任意一点,DE∥BC交AC于点E。△ADE
和△ABC还相似吗?△ADE∽△ABC探究活动二:相似三角形的判定的预备定理: 如果点D在AB所在的直线上,继续改变点D的位置。
DE∥BC交AC于点E。△ADE和△ABC还相似吗?∵DE∥BC
∴△ADE∽△ABC∵DE∥BC
∴△ADE∽△ABC探究活动三:考考你的眼力! 如图: ABCD,E是AB延长线上一点。DE与AC和
BC分别相交于点O、F。你能找出图中的相似三角形吗?
并说明理由。∴△BDM∽△BCA应用举例解:∵MD∥AC,又∵ ME∥AB,∴△CEM∽△CAB3份学以致用如图:一条河流,在河流的北岸点A处有一根高压电线杆。河流的南岸点B处有一颗大树。且电线杆在大树的正北方向上。在大树的正东方的点C处有一雕像,你能利用本节课学习的知识大致测算出电线杆A与大树B之间的距离吗? 若用皮尺测得:BC=50米,CD=20米,DE=60米,你能计算出电线杆A与大树B之间的距离吗?ABCDE你学会了什么?∵DE∥BC
∴△ADE∽△ABC1、相似三角形的判定方法:由平行得相似。2、相似三角形性质的应用。谢谢同学们!ABCDEB3B2B1C1C2C3FHMNa4a3aaaaaa2a3、如图:在△ABC中,DE∥BC,
BE与DC相交于点O。OD = 2 cm,
OC = 4 cm,AC = 10 cm。
求:AE的长。
