2012-2013学年度九年级上学期数学期中试题及答案
文档属性
| 名称 | 2012-2013学年度九年级上学期数学期中试题及答案 |  | |
| 格式 | zip | ||
| 文件大小 | 175.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-02 20:45:13 | ||
图片预览


文档简介
一、选择题(每小题3分,共60分)
1.下列方程中,一元二次方程共有( ).
① ② ③ ④⑤
A. 2个 B.3个 C.4个 D. 5个
2.一元二次方程的根是( ).
A. B. C. D.
3.如图,下列四组条件中.不能判定四边形ABCD是平行四边形的是( ).
A、AB=DC,AD=BC B、AB∥DC,AD∥BC
C、AB∥DC,AD=BC D、AB∥DC,AB=DC
4.下列关于矩形的说法,正确的是( ).
A.对角线相等的四边形是矩形 B.对角线互相平分的四边形是矩形
C.矩形的对角线互相垂直且平分 D.矩形的对角线相等且互相平分
5.用直尺和圆规作一个菱形,如图,能得到四边形ABCD是菱形的依据是( ).
A.一组邻边相等的四边形是菱形
B.四边都相等的四边形是菱形
C.对角线互相垂直的平行四边形是菱形
D.每条对角线平分一组对角的平行四边形是菱形
6.一元二次方程x2-x+2=0的根的情况是( ).
A.有两个相等的实数根 B.有两个不相等的实数根
C.无实数根 D.只有一个实数根
7.下列命题中,不正确的是( )
A.关于轴对称的两个图形是全等形
B.关于中心对称的两个图形是全等形
C.全等的两个三角形成中心对称
D.成中心对称的两个图形的对称点连线经过对称中心
8.如图,在△ABC中,BD、CE是△ABC的中线,BD与CE相交于点O,点F、G 分别是BO、 CO的中点,连结AO.若AO=6cm,BC=8cm,则四边形DEFG的周长是 ( ).
A. 14cm B. 18 cm C. 24cm D. 28cm
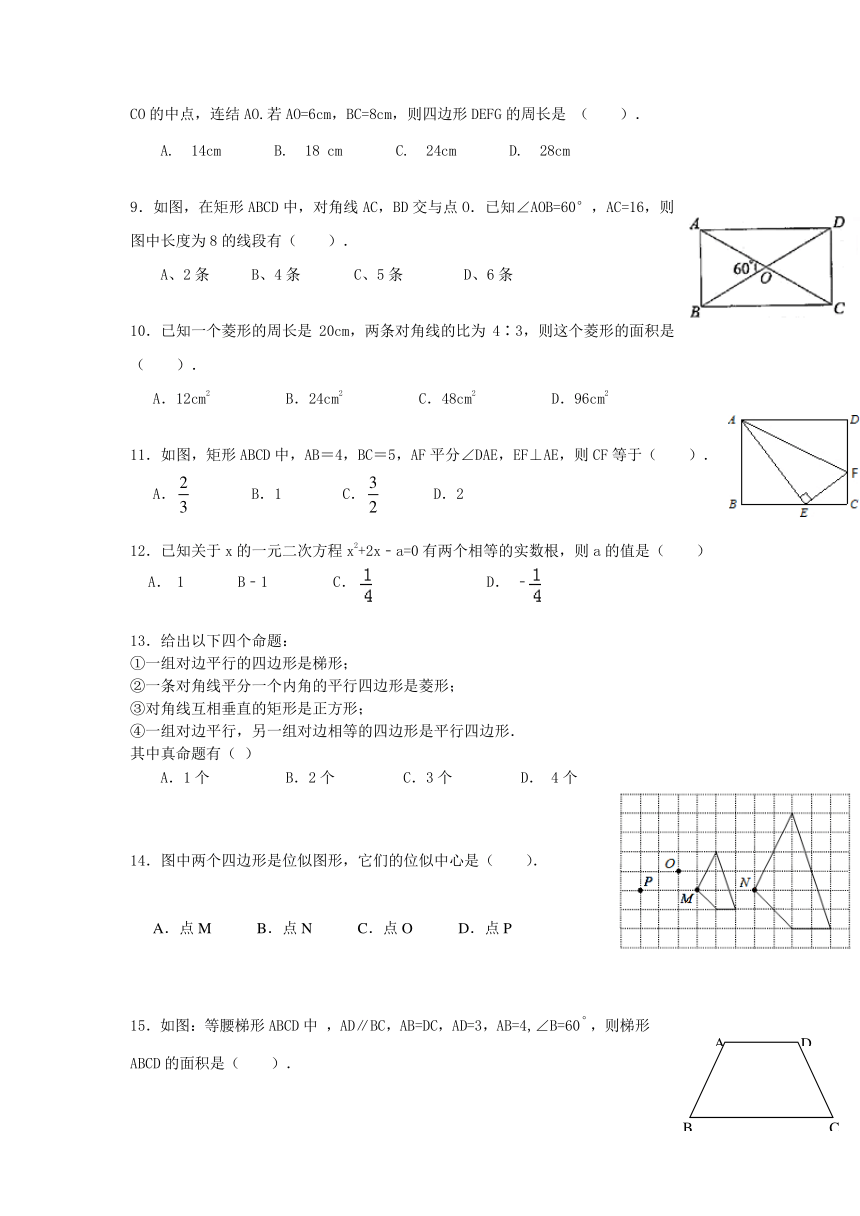
9.如图,在矩形ABCD中,对角线AC,BD交与点O.已知∠AOB=60°,AC=16,则图中长度为8的线段有( ).
A、2条 B、4条 C、5条 D、6条
10.已知一个菱形的周长是20cm,两条对角线的比为4∶3,则这个菱形的面积是( ).
A.12cm2 B.24cm2 C.48cm2 D.96cm2
11.如图,矩形ABCD中,AB=4,BC=5,AF平分∠DAE,EF⊥AE,则CF等于( ).
A. B.1 C. D.2
12.已知关于x的一元二次方程x2+2x﹣a=0有两个相等的实数根,则a的值是( )
A. 1 B﹣1 C. D. ﹣
13.给出以下四个命题:
①一组对边平行的四边形是梯形;
②一条对角线平分一个内角的平行四边形是菱形;
③对角线互相垂直的矩形是正方形;
④一组对边平行,另一组对边相等的四边形是平行四边形.
其中真命题有( )
A.1个 B.2个 C.3个 D. 4个
14.图中两个四边形是位似图形,它们的位似中心是( ).
A.点M B.点N C.点O D.点P
15.如图:等腰梯形ABCD中 ,AD∥BC,AB=DC,AD=3,AB=4,∠B=60,则梯形ABCD的面积是( ).
A. B.
C. D.
16.对于任意实数x,x2-4x+7的值是一个( )
A 负数 B 非正数 C 正数 D 不确定
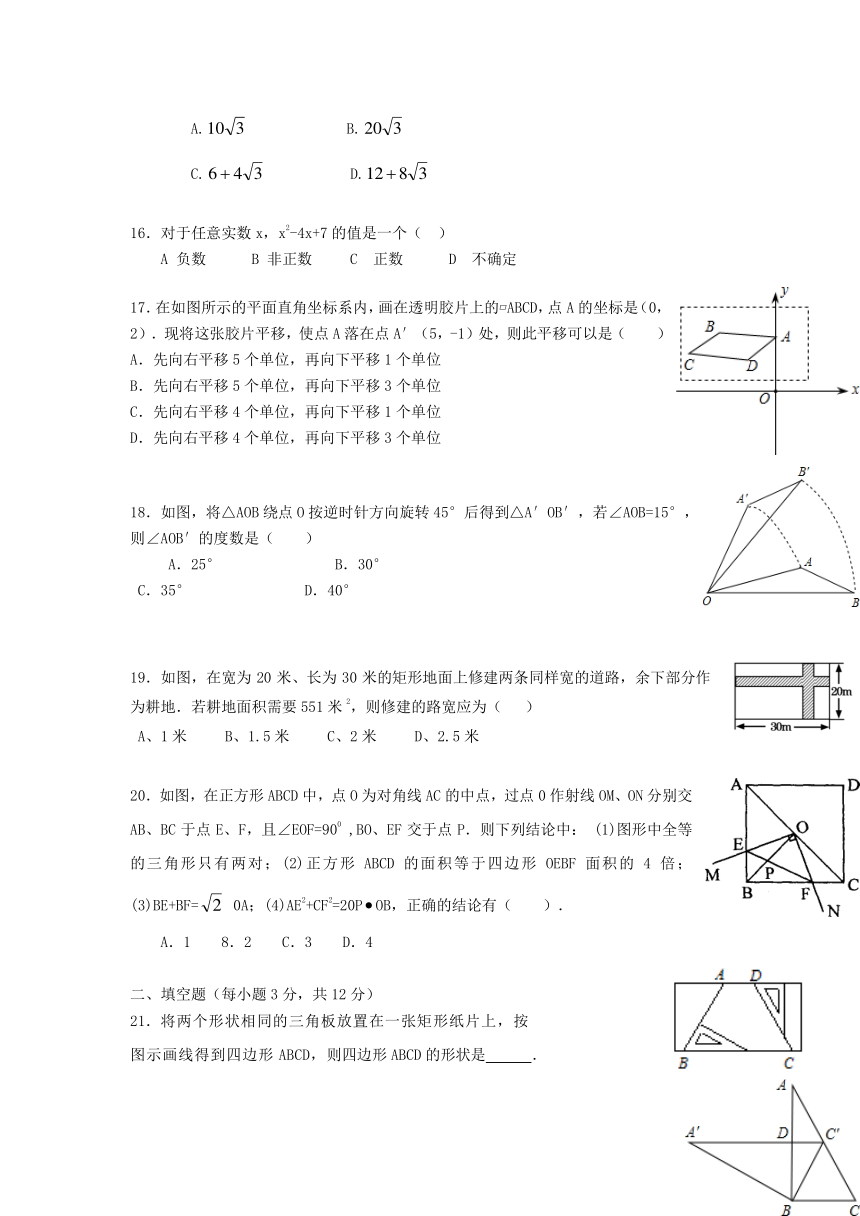
17.在如图所示的平面直角坐标系内,画在透明胶片上的 ABCD,点A的坐标是(0,2).现将这张胶片平移,使点A落在点A′(5,-1)处,则此平移可以是( )
A.先向右平移5个单位,再向下平移1个单位
B.先向右平移5个单位,再向下平移3个单位
C.先向右平移4个单位,再向下平移1个单位
D.先向右平移4个单位,再向下平移3个单位
18.如图,将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′,若∠AOB=15°,则∠AOB′的度数是( )
A.25° B.30°
C.35° D.40°
19.如图,在宽为20米、长为30米的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551米2,则修建的路宽应为( )
A、1米 B、1.5米 C、2米 D、2.5米
20.如图,在正方形ABCD中,点O为对角线AC的中点,过点0作射线OM、ON分别交AB、BC于点E、F,且∠EOF=900 ,BO、EF交于点P.则下列结论中: (1)图形中全等的三角形只有两对;(2)正方形ABCD的面积等于四边形OEBF面积的4倍;(3)BE+BF= 0A;(4)AE2+CF2=20POB,正确的结论有( ).
A.1 8.2 C.3 D.4
二、填空题(每小题3分,共12分)
21.将两个形状相同的三角板放置在一张矩形纸片上,按
图示画线得到四边形ABCD,则四边形ABCD的形状是 .
22.如图,两块相同的三角板完全重合在一起,∠A=30°,AC=10,把上面一块绕直角顶点B逆时针旋转到△A′BC′的位置,点C′在AC上,A′C ′与AB相交于点D,则C′D= .
23.写一个以2和-3为根的一元二次方程 .
24.已知ABCD的周长为28,自顶点A作AE⊥DC于点E,AF⊥BC于点F. 若AE=3,AF=4,则 CE-CF= .
三、解答题(共48分)
25.解方程(每小题5分,共10分)
(1) 3x2 -9x+2=0(配方法) (2)(3x+2)(x+3)=x+14
26.如图,已知四边形ABCD为平行四边形,AE⊥BD于E,CF⊥BD于F.
(1) 求证:BE = DF;(6分)
(2) 若 M、N分别为边AD、BC上的点,且DM=BN,试判断四边形MENF的形 状(不必说明理由).(2分)
27.近年来,某县为发展教育事业,加大了对教育经费的投入,2009年投入6000万元,2011年投入8640万元.
(1)求2009年至2011年该县投入教育经费的年平均增长率;(6分)
(2)该县预计2012年投入教育经费不低于9500万元,若继续保持前两年的平均增长率,该目标能否实现?请通过计算说明理由.(2分)
28.已知:在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,E是BC的中点,连接AE、AC.
(1)点F是DC上一点,连接EF,交AC于点O(如图1),求证:△AOE∽△COF;(4分)
(2)若点F是DC的中点,连接BD,交AE与点G(如图2),求证:四边形EFDG是菱形.(6分)
29.如图,在梯形ABCD中,AD∥BC,AD=AB,过点A作AE∥DB交CB的延长线于点E.
(1)求证:∠ABD=∠CBD;(4分)
(2)若∠C=2∠E,求证:AB=DC;(4分)
(3)在(2)的条件下,sinC=,AD=,求四边形AEBD的面积.(4分)
附加题:
在一次研究性学习活动中,某小组将两张互相重合的正方形纸片ABCD和EFGH的中心O用图钉固定住,保持正方形ABCD不动,顺时针旋转正方形EFGH,如图所示.
(1)小组成员经观察、测量,发现在旋转过程中,有许多有趣的结论. 下面是旋转角度小于90°时他们得到的一些猜想:①ME=MA;②两张正方形纸片的重叠部分的面积为定值;③∠MON保持45°不变.
请你对这三个猜想做出判断(正确的在序号后的括号内打上“√”,错误的打上“×”):
①( );②( );③( ).
(2)小组成员还发现:(1)中的△EMN的面积S随着旋转角度∠AOE的变化而变化. 请你指出在怎样的位置时△EMN的面积S取得最大值. (不必证明)
(3)上面的三个猜想中若有正确的,请选择其中的一个给予证明;若都是错误的,请选择其一说明理由.
答案:1—5 :BCCDB 6—10:CCADB 11—15:CBBDA 16—20:CBBAC
21.将两个形状相同的三角板放置在一张矩形纸片上,按
图示画线得到四边形ABCD,则四边形ABCD的形状是 等腰梯形 .
22.如图,两块相同的三角板完全重合在一起,∠A=30°,AC=10,把上面一块绕直角顶点B逆时针旋转到△A′BC′的位置,点C′在AC上,A′C ′与AB相交于点D,则C′D= 2.5 .
23.写一个以2和-3为根的一元二次方程 (x-2)(x+3)=0 .
24.已知ABCD的周长为28,自顶点A作AE⊥DC于点E,AF⊥BC于点F. 若AE=3,AF=4,则 CE-CF= .
【答案】2+或2-。
【分析】由平行四边形对角相等的性质,得∠D=∠B,由AE⊥DC,AF⊥BC,得Rt△ADE∽Rt△ABF,得。
所以设AD=3,AB=4,由ABCD的周长为28和对边相等的性质,得2(3+4)=28,解得=2。因此,AD=BC=6,AB=DC=8。
由勾股定理,可求得DE=3,BF=4。
下面分两种情况讨论:
情况1.如图,点E在DC上,点F在BC上,
CE-CF=(DC-DE)-(BC-BF)=(8-3)-(6-4)
=2+。
情况2.如图,点E在CD延长线上,点F在CB延长线上,
CE-CF=(DC+DE)-(BC+BF)=(8+3)-(6+4)
=2-。
综上所述,CE-CF=2+或2-。
25—27略
28.(1)证明:∵点E是BC的中点,BC=2AD
∴EC=BE=BC=AD 又∵AD∥DC
∴四边形AECD为平行四边形………………………………………………2分
∴AE∥DC ∴∠AEO=∠CFO,∠EAO=∠FCO
∴△AOE∽△COF……………………………………………………………4分
(2)证明:连接DE
∵DE平行且等于BE ∴四边形ABED是平行四边形
又∠ABE=90° ∴ABED是矩形
∴GE=GA=GB=GD=BD=AE……………………………………………6分
∴E、F分别是BC、CD的中点 ∴EF、GE是△CBD的两条中线
∴EF=BD=GD,GE=CD=DF……………………………………………8分
又GE=GD ∴EF=GD=GE=DF
∴四边形EFDG是菱形……………………………………………………10分
29.解:(1)证明:∵AD∥BC,∴∠ADB=∠CBD。
∵AB=AD,∴∠ADB=∠ABD,∴∠ABD=∠CBD。
(2)证明:∵AE∥DB,∴∠E=∠CBD。
由(1)得∠ABD=∠CBD,∴∠ABC=2∠CBD=2∠E。
又∵∠C=2∠E,∴∠ABC=∠C。
∴在梯形ABCD中, AB=DC。
(3)过D作DF⊥BC,垂足为F,由sinC=,得=。
由(2)有CD=AB,又AB=AD=,
∴ CD=,DF= eq \f(4,5)。
∵AD∥BC,AE∥DB,
∴四边形AEBD的平行四边形。
∴S四边形AEBD=AD·DF=× eq \f(4,5)=。
附加题:
(1)①(√);②(×);③(√).
(2)当∠AOE=45°时,△EMN的面积S取得最大值.
(3)证明:对于猜想①,连结OA、OE、AE. 由已知得OA=OE,∴∠OAE=∠OEA.
又∵∠OAM=∠OEM=45°,∴∠OAE-∠OAM=∠OEA-∠OEM,即∠MAE=∠MEA. ∴ME=MA.
对于猜想③,证得OM平分∠EOA,同理ON平分∠DOE,
∴∠MOE+∠NOE=∠AOD=×90°=45°,即∠MON保持45°不变.
A D
B C
1.下列方程中,一元二次方程共有( ).
① ② ③ ④⑤
A. 2个 B.3个 C.4个 D. 5个
2.一元二次方程的根是( ).
A. B. C. D.
3.如图,下列四组条件中.不能判定四边形ABCD是平行四边形的是( ).
A、AB=DC,AD=BC B、AB∥DC,AD∥BC
C、AB∥DC,AD=BC D、AB∥DC,AB=DC
4.下列关于矩形的说法,正确的是( ).
A.对角线相等的四边形是矩形 B.对角线互相平分的四边形是矩形
C.矩形的对角线互相垂直且平分 D.矩形的对角线相等且互相平分
5.用直尺和圆规作一个菱形,如图,能得到四边形ABCD是菱形的依据是( ).
A.一组邻边相等的四边形是菱形
B.四边都相等的四边形是菱形
C.对角线互相垂直的平行四边形是菱形
D.每条对角线平分一组对角的平行四边形是菱形
6.一元二次方程x2-x+2=0的根的情况是( ).
A.有两个相等的实数根 B.有两个不相等的实数根
C.无实数根 D.只有一个实数根
7.下列命题中,不正确的是( )
A.关于轴对称的两个图形是全等形
B.关于中心对称的两个图形是全等形
C.全等的两个三角形成中心对称
D.成中心对称的两个图形的对称点连线经过对称中心
8.如图,在△ABC中,BD、CE是△ABC的中线,BD与CE相交于点O,点F、G 分别是BO、 CO的中点,连结AO.若AO=6cm,BC=8cm,则四边形DEFG的周长是 ( ).
A. 14cm B. 18 cm C. 24cm D. 28cm
9.如图,在矩形ABCD中,对角线AC,BD交与点O.已知∠AOB=60°,AC=16,则图中长度为8的线段有( ).
A、2条 B、4条 C、5条 D、6条
10.已知一个菱形的周长是20cm,两条对角线的比为4∶3,则这个菱形的面积是( ).
A.12cm2 B.24cm2 C.48cm2 D.96cm2
11.如图,矩形ABCD中,AB=4,BC=5,AF平分∠DAE,EF⊥AE,则CF等于( ).
A. B.1 C. D.2
12.已知关于x的一元二次方程x2+2x﹣a=0有两个相等的实数根,则a的值是( )
A. 1 B﹣1 C. D. ﹣
13.给出以下四个命题:
①一组对边平行的四边形是梯形;
②一条对角线平分一个内角的平行四边形是菱形;
③对角线互相垂直的矩形是正方形;
④一组对边平行,另一组对边相等的四边形是平行四边形.
其中真命题有( )
A.1个 B.2个 C.3个 D. 4个
14.图中两个四边形是位似图形,它们的位似中心是( ).
A.点M B.点N C.点O D.点P
15.如图:等腰梯形ABCD中 ,AD∥BC,AB=DC,AD=3,AB=4,∠B=60,则梯形ABCD的面积是( ).
A. B.
C. D.
16.对于任意实数x,x2-4x+7的值是一个( )
A 负数 B 非正数 C 正数 D 不确定
17.在如图所示的平面直角坐标系内,画在透明胶片上的 ABCD,点A的坐标是(0,2).现将这张胶片平移,使点A落在点A′(5,-1)处,则此平移可以是( )
A.先向右平移5个单位,再向下平移1个单位
B.先向右平移5个单位,再向下平移3个单位
C.先向右平移4个单位,再向下平移1个单位
D.先向右平移4个单位,再向下平移3个单位
18.如图,将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′,若∠AOB=15°,则∠AOB′的度数是( )
A.25° B.30°
C.35° D.40°
19.如图,在宽为20米、长为30米的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551米2,则修建的路宽应为( )
A、1米 B、1.5米 C、2米 D、2.5米
20.如图,在正方形ABCD中,点O为对角线AC的中点,过点0作射线OM、ON分别交AB、BC于点E、F,且∠EOF=900 ,BO、EF交于点P.则下列结论中: (1)图形中全等的三角形只有两对;(2)正方形ABCD的面积等于四边形OEBF面积的4倍;(3)BE+BF= 0A;(4)AE2+CF2=20POB,正确的结论有( ).
A.1 8.2 C.3 D.4
二、填空题(每小题3分,共12分)
21.将两个形状相同的三角板放置在一张矩形纸片上,按
图示画线得到四边形ABCD,则四边形ABCD的形状是 .
22.如图,两块相同的三角板完全重合在一起,∠A=30°,AC=10,把上面一块绕直角顶点B逆时针旋转到△A′BC′的位置,点C′在AC上,A′C ′与AB相交于点D,则C′D= .
23.写一个以2和-3为根的一元二次方程 .
24.已知ABCD的周长为28,自顶点A作AE⊥DC于点E,AF⊥BC于点F. 若AE=3,AF=4,则 CE-CF= .
三、解答题(共48分)
25.解方程(每小题5分,共10分)
(1) 3x2 -9x+2=0(配方法) (2)(3x+2)(x+3)=x+14
26.如图,已知四边形ABCD为平行四边形,AE⊥BD于E,CF⊥BD于F.
(1) 求证:BE = DF;(6分)
(2) 若 M、N分别为边AD、BC上的点,且DM=BN,试判断四边形MENF的形 状(不必说明理由).(2分)
27.近年来,某县为发展教育事业,加大了对教育经费的投入,2009年投入6000万元,2011年投入8640万元.
(1)求2009年至2011年该县投入教育经费的年平均增长率;(6分)
(2)该县预计2012年投入教育经费不低于9500万元,若继续保持前两年的平均增长率,该目标能否实现?请通过计算说明理由.(2分)
28.已知:在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,E是BC的中点,连接AE、AC.
(1)点F是DC上一点,连接EF,交AC于点O(如图1),求证:△AOE∽△COF;(4分)
(2)若点F是DC的中点,连接BD,交AE与点G(如图2),求证:四边形EFDG是菱形.(6分)
29.如图,在梯形ABCD中,AD∥BC,AD=AB,过点A作AE∥DB交CB的延长线于点E.
(1)求证:∠ABD=∠CBD;(4分)
(2)若∠C=2∠E,求证:AB=DC;(4分)
(3)在(2)的条件下,sinC=,AD=,求四边形AEBD的面积.(4分)
附加题:
在一次研究性学习活动中,某小组将两张互相重合的正方形纸片ABCD和EFGH的中心O用图钉固定住,保持正方形ABCD不动,顺时针旋转正方形EFGH,如图所示.
(1)小组成员经观察、测量,发现在旋转过程中,有许多有趣的结论. 下面是旋转角度小于90°时他们得到的一些猜想:①ME=MA;②两张正方形纸片的重叠部分的面积为定值;③∠MON保持45°不变.
请你对这三个猜想做出判断(正确的在序号后的括号内打上“√”,错误的打上“×”):
①( );②( );③( ).
(2)小组成员还发现:(1)中的△EMN的面积S随着旋转角度∠AOE的变化而变化. 请你指出在怎样的位置时△EMN的面积S取得最大值. (不必证明)
(3)上面的三个猜想中若有正确的,请选择其中的一个给予证明;若都是错误的,请选择其一说明理由.
答案:1—5 :BCCDB 6—10:CCADB 11—15:CBBDA 16—20:CBBAC
21.将两个形状相同的三角板放置在一张矩形纸片上,按
图示画线得到四边形ABCD,则四边形ABCD的形状是 等腰梯形 .
22.如图,两块相同的三角板完全重合在一起,∠A=30°,AC=10,把上面一块绕直角顶点B逆时针旋转到△A′BC′的位置,点C′在AC上,A′C ′与AB相交于点D,则C′D= 2.5 .
23.写一个以2和-3为根的一元二次方程 (x-2)(x+3)=0 .
24.已知ABCD的周长为28,自顶点A作AE⊥DC于点E,AF⊥BC于点F. 若AE=3,AF=4,则 CE-CF= .
【答案】2+或2-。
【分析】由平行四边形对角相等的性质,得∠D=∠B,由AE⊥DC,AF⊥BC,得Rt△ADE∽Rt△ABF,得。
所以设AD=3,AB=4,由ABCD的周长为28和对边相等的性质,得2(3+4)=28,解得=2。因此,AD=BC=6,AB=DC=8。
由勾股定理,可求得DE=3,BF=4。
下面分两种情况讨论:
情况1.如图,点E在DC上,点F在BC上,
CE-CF=(DC-DE)-(BC-BF)=(8-3)-(6-4)
=2+。
情况2.如图,点E在CD延长线上,点F在CB延长线上,
CE-CF=(DC+DE)-(BC+BF)=(8+3)-(6+4)
=2-。
综上所述,CE-CF=2+或2-。
25—27略
28.(1)证明:∵点E是BC的中点,BC=2AD
∴EC=BE=BC=AD 又∵AD∥DC
∴四边形AECD为平行四边形………………………………………………2分
∴AE∥DC ∴∠AEO=∠CFO,∠EAO=∠FCO
∴△AOE∽△COF……………………………………………………………4分
(2)证明:连接DE
∵DE平行且等于BE ∴四边形ABED是平行四边形
又∠ABE=90° ∴ABED是矩形
∴GE=GA=GB=GD=BD=AE……………………………………………6分
∴E、F分别是BC、CD的中点 ∴EF、GE是△CBD的两条中线
∴EF=BD=GD,GE=CD=DF……………………………………………8分
又GE=GD ∴EF=GD=GE=DF
∴四边形EFDG是菱形……………………………………………………10分
29.解:(1)证明:∵AD∥BC,∴∠ADB=∠CBD。
∵AB=AD,∴∠ADB=∠ABD,∴∠ABD=∠CBD。
(2)证明:∵AE∥DB,∴∠E=∠CBD。
由(1)得∠ABD=∠CBD,∴∠ABC=2∠CBD=2∠E。
又∵∠C=2∠E,∴∠ABC=∠C。
∴在梯形ABCD中, AB=DC。
(3)过D作DF⊥BC,垂足为F,由sinC=,得=。
由(2)有CD=AB,又AB=AD=,
∴ CD=,DF= eq \f(4,5)。
∵AD∥BC,AE∥DB,
∴四边形AEBD的平行四边形。
∴S四边形AEBD=AD·DF=× eq \f(4,5)=。
附加题:
(1)①(√);②(×);③(√).
(2)当∠AOE=45°时,△EMN的面积S取得最大值.
(3)证明:对于猜想①,连结OA、OE、AE. 由已知得OA=OE,∴∠OAE=∠OEA.
又∵∠OAM=∠OEM=45°,∴∠OAE-∠OAM=∠OEA-∠OEM,即∠MAE=∠MEA. ∴ME=MA.
对于猜想③,证得OM平分∠EOA,同理ON平分∠DOE,
∴∠MOE+∠NOE=∠AOD=×90°=45°,即∠MON保持45°不变.
A D
B C
同课章节目录
