2013-2014学年青岛版九年级下学期数学期末检测题含答案解析
文档属性
| 名称 | 2013-2014学年青岛版九年级下学期数学期末检测题含答案解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 198.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-02 00:00:00 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
期末检测题
(本检测题满分:120分,时间:120分钟)
一、选择题(每小题3分,共36分)
1. 若在函数中,随的增大而增大,且,则它的图象大致是( )
2.直线交坐标轴于两点,则不等式的解集
为( )
A. B. C. D.
3. 设点A(x1,y1)和B(x2,y2)是反比例函数y=图象上的两个点,当x1<x2<0时,y1<y2,则一次函数y=-2x+k的图象不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.对于函数,下列结论错误的是( )
A.当时,随的增大而增大
B.当时,随的增大而增大
C.时的函数值大于时的函数值
D.在函数图象所在的每个象限内,随的增大而增大
5. 如果关于x的一元二次方程kx2-2x-1=0有两个不相等的实数根,那么实数k的取值范围 是( )
A.k>-1 B.k<1且k≠0
C.k≥-1且k≠0 D.k>-1且k≠0
6. 已知一个直角三角形的两条直角边长恰好是方程的两个根,则这个直角三角形的斜边长是( )
A. B.3 C.6 D.9
7. 有五张卡片(形状、大小、质地都相同),上面分别画有下列图形:①线段;②正三角形;③平行四边形;④等腰梯形;⑤圆.将卡片背面朝上洗匀,从中任意抽取一张,正面图形一定满足既是轴对称图形又是中心对称图形的概率是( )
A. B. C. D.
8. 一个不透明的口袋里装有除颜色外都相同的5个白球和若干个红球,在不允许将球倒出来数的前提下,小亮为了估计其中的红球数,采用如下方法:先将口袋中的球摇匀,再从口袋里随机摸出一球,记下颜色,然后把它放回口袋中.不断重复上述过程.小亮共摸了100次,其中有10次摸到白球.因此小亮估计口袋中的红球大约有( )个.
A.45 B.48 C.50 D.55
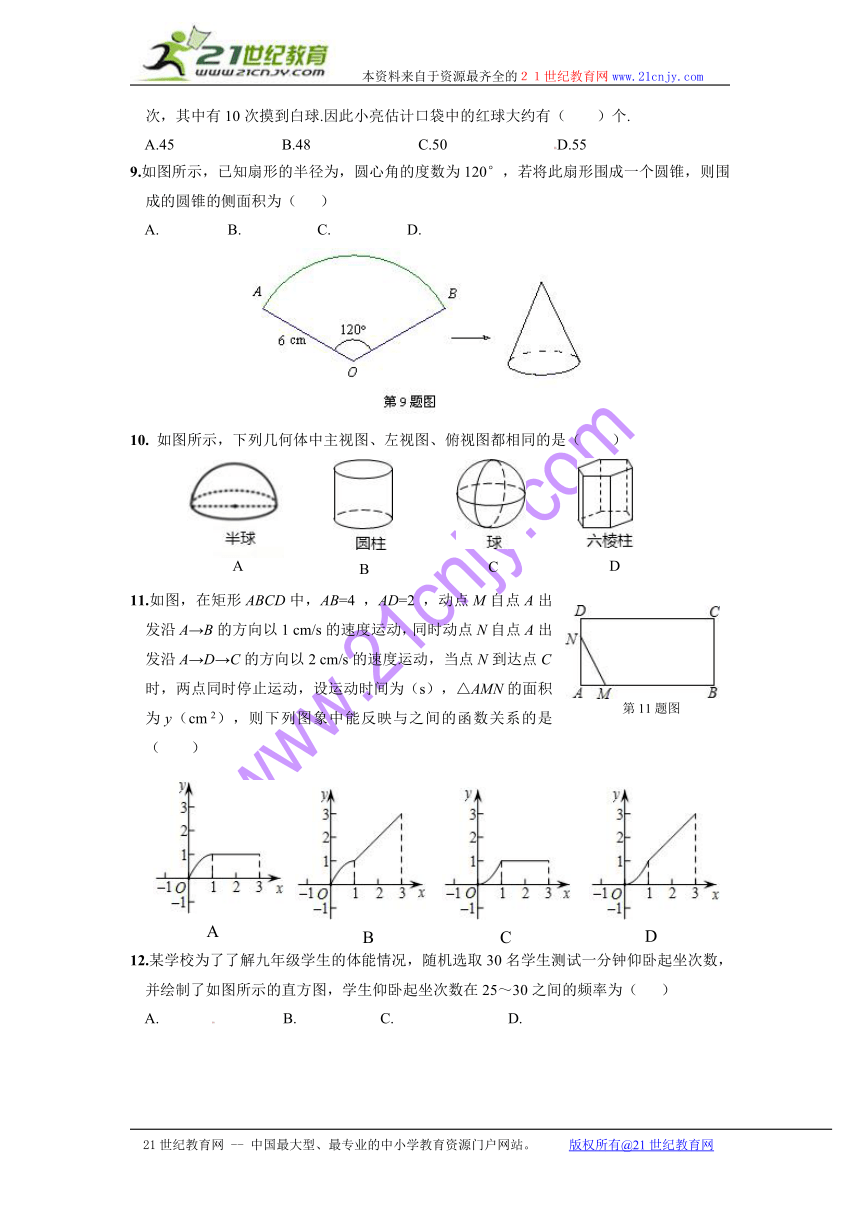
9.如图所示,已知扇形的半径为,圆心角的度数为120°,若将此扇形围成一个圆锥,则围成的圆锥的侧面积为( )
A. B. C. D.
10. 如图所示,下列几何体中主视图、左视图、俯视图都相同的是( )
11.如图,在矩形ABCD中,AB=4 ,AD=2 ,动点M自点A出发沿A→B的方向以1 cm/s的速度运动,同时动点N自点A出发沿A→D→C的方向以2 cm/s的速度运动,当点N到达点C时,两点同时停止运动,设运动时间为(s),△AMN的面积为y(cm 2),则下列图象中能反映与之间的函数关系的是( )
12.某学校为了了解九年级学生的体能情况,随机选取30名学生测试一分钟仰卧起坐次数,并绘制了如图所示的直方图,学生仰卧起坐次数在25~30之间的频率为( )
A. B. C. D.
二、填空题(每小题3分,共24分)
13. 把抛物线的图象向右平移3个单位长度,再向下平移2个单位长度,所得图象的解析式为,则的值为 .
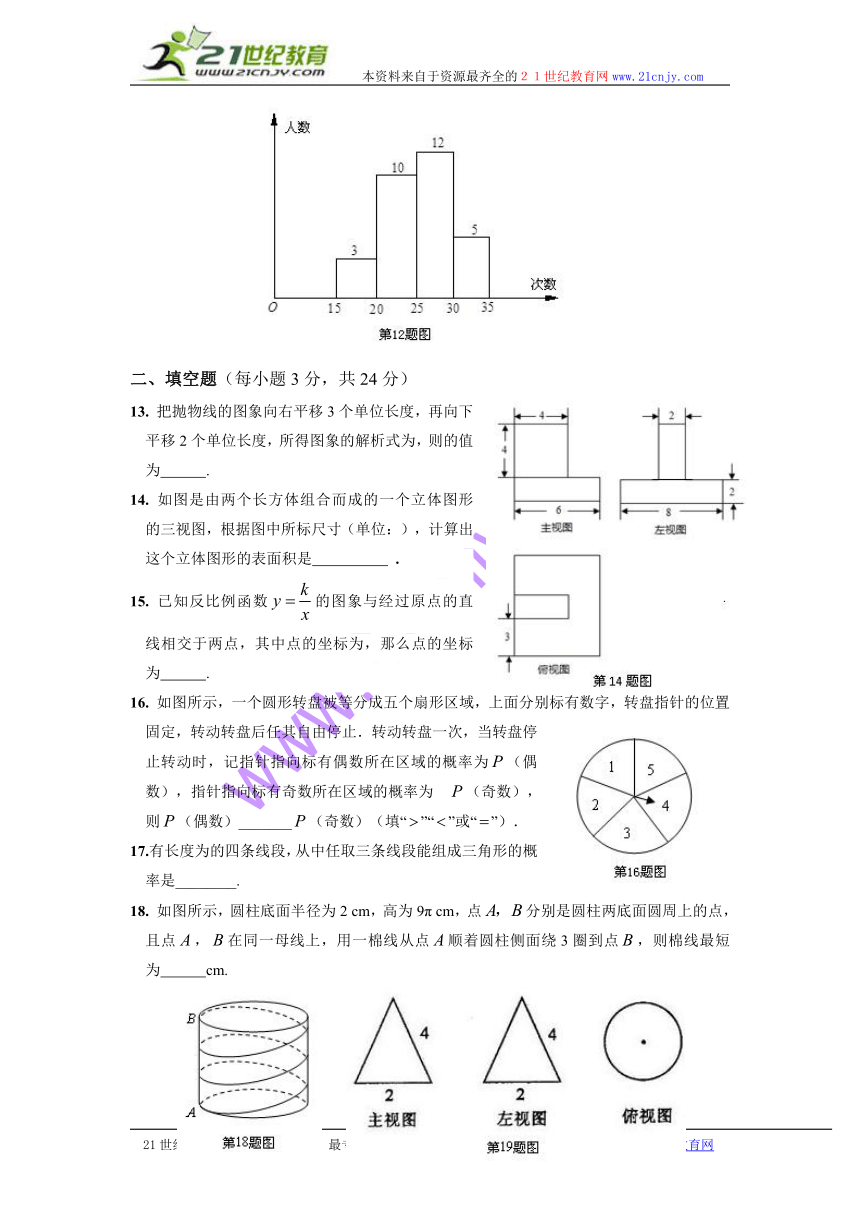
14. 如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸(单位:),计算出这个立体图形的表面积是200 .
15. 已知反比例函数的图象与经过原点的直线相交于两点,其中点的坐标为,那么点的坐标为 .
16. 如图所示,一个圆形转盘被等分成五个扇形区域,上面分别标有数字,转盘指针的位置固定,转动转盘后任其自由停止.转动转盘一次,当转盘停止转动时,记指针指向标有偶数所在区域的概率为(偶数),指针指向标有奇数所在区域的概率为 (奇数),则(偶数)_______(奇数)(填“”“”或“”).
17.有长度为的四条线段,从中任取三条线段能组成三角形的概率是________.
18. 如图所示,圆柱底面半径为2 cm,高为9π cm,点分别是圆柱两底面圆周上的点,且点,在同一母线上,用一棉线从点顺着圆柱侧面绕3圈到点,则棉线最短 为 cm.
19. 一个几何体的三视图如图所示,其中主视图和左视图都是腰长为4,底边长为2的等腰三角形,则这个几何体侧面展开图的面积为________.
20. 在同一平面内,下列4个函数:①②;③;④的图象不可能由函数的图象通过平移变换得到的是 .
三、解答题(共60分)
21. (7分)如图所示,已知反比例函数y1=的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
(1)求这两个函数的表达式;
(2)观察图象,当x>0时,直接写出y1>y2时自变量x的取值范围;
(3)如果点C与点A关于x轴对称,求△ABC的面积.
22. (7分)在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球,它们除颜色外完全相同,其中红球有2个,黄球有1个,蓝球有1个.现有一张电影票,小明和小亮决定通过摸球游戏定输赢(赢的一方获得电影票).游戏规则是:两人各摸1次球,先由小明从纸箱里随机摸出1个球,记录颜色后放回,将小球摇匀,再由小亮随机摸出1个球并记录颜色.若两人摸到的球颜色相同,则小明赢,否则小亮赢.这个游戏规则对双方公平吗?请你利用树状图或列表法说明理由.
23. (7分)在△ABC中,AB = ,AC = ,BC = 1.
(1)求证:∠A≠30°;
(2)将△ABC绕BC所在直线旋转一周,求所得几何体的表面积.
24. (7分)为了预防流感,某学校在休息日用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为(为常数).如图所示,根据图中提供的信息,解答下列问题:
(1)写出从药物释放开始,y与t之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米含药量降低到0.25毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?
25. (7分)为了了解小学生的体能情况,抽取了某小学同年级部分学生进行跳绳测试,将所得的数据整理后画出频数分布直方图,已知图中从左到右的前三个小组的频率分别是0.1,0.3,0.4,第一小组的频数是5.
(1)求第四小组的频率和参加这次测试的学生人数;
(2)在这次测试中,学生跳绳次数的中位数落在第几小组内?
26.(7分) 作出图中立体图形的三视图.
27.(8分)已知直四棱柱的底面是边长为a的正方形, 高为, 体积为V, 表面积为S.
(1) 当a = 2, h = 3时,分别求V和S;
(2) 当V = 12,S = 32时,求的值.
28.(10分)如图所示,抛物线经过原点O,与轴交于另一点N,直线与两坐标轴分别交于A,D两点,与抛物线交于B(1,3),C(2,2)两点.
(1)求直线与抛物线的解析式.
(2)若抛物线在轴上方的部分有一动点 P(,),求△PON面积的最大值.
(3)若动点P保持(2)中的运动路线,问是否存在点P,使得△POA的面积等于△POD面积的?若存在,请求出点P的坐标;若不存在,请说明理由.
期末检测题参考答案
1.B 解析:由随的增大而增大,知函数的图象由左至右上升,故k>0;又由,知函数的图象与轴的负半轴相交.
2.A 解析:由直线交坐标轴于两点,
知所以
解,得
3. A 解析:本题考查了反比例函数、一次函数的图象和性质.对于反比例函数,∵ x1<x2<0时,y1<y2,说明在同一个象限内,y随x的增大而增大,∴ k<0.∴ 一次函数y=-2x+k的图象与y轴交于负半轴,其图象经过第二、三、四象限,不经过第一象限.
4.C 解析:A.当时,的图象位于第四象限,随的增大而增大,正确;
B.当时,的图象位于第二象限,随的增大而增大,正确;
C.时的函数值为,时的函数值为,故时的函数值小于时的函数值,错误;
D.根据A,B可知,正确.
5. D 解析:∵ 一元二次方程kx2-2x-1=0有两个不相等的实数根,∴ Δ=b2-4ac=4+4k>0,且k≠0,解得k>-1且k≠0.
点拨:此题考查了一元二次方程根的判别式,根的判别式的值大于0,方程有两个不相等的实数根;根的判别式的值等于0,方程有两个相等的实数根;根的判别式的值小于0,方程没有实数根.本题在求k的取值范围时要注意二次项系数不为0的条件.
6. B 解析1:∵
∴ x==,∴ =+
∴ 这个直角三角形的斜边长是3,故选B.
解析2:设和是方程的两个根,
由一元二次方程根与系数的关系可得
∴ ,
∴ 这个直角三角形的斜边长是3,故选B.
7. B 解析:既是轴对称图形又是中心对称图形的有线段、圆,共2张,所以所求概率为.
8. A 解析:本题考查了简单随机事件的概率计算,设口袋中有x个红球,由题意得,P(摸到白球)==,解得x=45.
9. D 解析: .
10. C 解析:A.此半球的三视图分别为半圆拱形、半圆拱形、圆,不符合题意;
B.圆柱的三视图分别为长方形、长方形、圆,不符合题意;
C.球的三视图都是圆,符合题意;
D.六棱柱的三视图不相同,不符合题意.
故选C.
11. D 解析:在矩形ABCD中,AB =4 ,AD =2 cm,
AD +DC =AB +AD = 4+2= 6(cm).
∵ 点M以1 cm/s的速度运动,∴ 4÷1=4(s).
∵ 点N以2 cm/s的速度运动,∴ 6÷2=3(s),
∴ 点N先到达终点,运动时间为3 s.
①点N在AD上运动时,=AM AN= 2=(0≤≤1);
②点N在DC上运动时,=AM AD= 2= (1≤3).
∴ 能反映与之间的函数关系的是选项D.故选D.
12. D 解析:因为学生仰卧起坐次数在25~30之间的人数为12,所以学生仰卧起坐次数在25~30之间的频率为,故选D.
13. 解析:∵ =,
∴ 抛物线顶点坐标为(1,2).
依题意,得平移前抛物线顶点坐标为(-2,4),
∵ 平移不改变二次项系数,
∴ ,
比较系数,得.
14. 200 解析:根据三视图可得:上面的长方体长4 mm,高4 mm,宽2 mm,下面的长方体底面两边长分别为6 mm,8 mm,高为2 mm,∴ 立体图形的表面积是(mm 2).
15.(-2,-1) 解析:设直线的解析式为,因为直线和反比例函数的图象都经过点,将点的坐标代入可得,,故直线的解析式为,反比例函数的解析式为,联立可解得点的坐标为(-2,-1).
16. 解析:因为 , ,所以.
17. 解析:从长度为的四条线段中任取三条有四种情况: .
其中不能组成三角形,故从中任取三条线段能组成三角形的概率是.
18. 15π 解析:要求圆柱体侧面上两点之间的最短路径,最直 接的作法,就是将圆柱体侧面展开,然后利用两点之间线段最短解答.圆柱体侧面的展开图如图所示:用一棉线从点A顺着圆柱侧面绕3圈到点B的最短路径是:AC→CD→DB,即在圆柱体的侧面展开图长方形中,将长方形平均分成3个小长方形,点A沿着3个小长方形的对角线运动到点B的路线最短.
∵ 圆柱底面半径为2 cm,
∴ 长方形的宽即圆柱体的底面圆周长是2π×2=4π(cm).
又∵ 圆柱高为9π cm,∴ 小长方形的一条边长是3π cm.
根据勾股定理求得AC=CD=DB=5π cm,
∴ AC+CD+DB=15π cm.
19. 4π 解析:由几何体的主视图和左视图都是等腰三角形,
俯视图是带圆心的圆,可以判断这个几何体是圆锥.
依题意知母线长l=4,底面半径r=1,
则由圆锥的侧面积公式得S=πrl=π×1×4=4π.
20. ③④ 解析:能通过平移变换互相得到的二次函数的图象,其解析式的二次项系数相同.二次项的系数不是2的函数有③④.
21. 分析:(1)先把点A(1,4)的坐标代入y1=,求出k的值;再把点B(m,-2)的坐标代入y1=,求出m的值;最后把A,B两点的坐标分别代入y2=ax+b,组成关于a,b的二元一次方程组,解方程组求出a,b即可.(2)由图象可以看出,当0<x<1时,y1所对应的图象在y2所对应图象的上方.(3)由题意,得AC=8,点B到AC的距离是点B的横坐标与点A的横坐标之差的绝对值,即等于3,所以S△ABC=×8×3=12.
解:(1)∵ 点A(1,4)在y1=的图象上,
∴ k=1×4=4,∴ y1=.
∵ 点B在y1=的图象上,
∴ m=-2,
∴ 点B(-2,-2).
又∵ 点A,B在一次函数y2=ax+b的图象上,
∴ 解得 ∴ y2=2x+2.
∴ 这两个函数的表达式分别为y1=,y2=2x+2.
(2)由图象可知,当x>0,y1>y2时,自变量x的取值范围为0<x<1.
(3)∵ 点C与点A关于x轴对称,∴ C(1,-4).
如图所示,过点B作BD⊥AC,垂足为D,则D(1,-2),
于是△ABC的高BD=|1-(-2)|=3,底边AC=|4-(-4)|=8 .
∴ S△ABC=AC·BD=×8×3=12.
点拨:两个函数图象交点处的函数值相等,在交点的同侧,函数图象越高,函数值就越大.
22. 解:游戏规则对双方不公平.理由如下:
树状图如图所示.
第22题答图
或列表为:
红 红 黄 蓝
红 (红,红) (红,红) (红,黄) (红,蓝)
红 (红,红) (红,红) (红,黄) (红,蓝)
黄 (黄,红) (黄,红) (黄,黄) (黄,蓝)
蓝 (蓝,红) (蓝,红) (蓝,黄) (蓝,蓝)
由上述树状图或表格知:所有出现的等可能结果共有16种.
∴ P(小明赢)=,P(小亮赢)=错误!未指定书签。.
∴ 此游戏对双方不公平,小亮赢的可能性大.
23. 分析:(1)根据勾股定理的逆定理得到△ABC是直角三角形,且∠C为直角,利用三角函数计算出sin A,然后与sin 30°进行比较即可判断∠A≠30°;
(2)将△ABC绕BC所在直线旋转一周,所得的几何体为圆锥,圆锥的底面圆的半径为AC,母线长为AB,所得几何体的表面积分为底面积和侧面积,分别根据圆的面积公式和扇形的面积公式进行计算即可.
(1)证明:∵ BC2+AC2=1+2=3=AB2,
∴ △ABC是直角三角形,且∠C为直角.
∵ 30°,
∴ ∠A≠30°.
(2)解:将△ABC绕BC所在直线旋转一周,所得的几何体为圆锥,
∴ 圆锥的底面圆的半径=,
∴ 圆锥的底面圆的周长=2π =2π,母线长为,
∴ 几何体的表面积= 2π +π =(+2)π.
24.解: (1) 将点的坐标代入函数关系式, 解得, 有.
将代入, 得, 所以所求反比例函数关系式为;
再将点的坐标代入, 得,
所以所求正比例函数关系式为.
(2) 解不等式 , 解得 ,所以至少需要经过6小时后,学生才能进入教室.
25. 解:(1)由题意知,前三个小组的频率分别是
则第四小组的频率为
又由第一小组的频数为,其频率为,
所以参加这次测试的学生人数为
(2)由可得,参加测试的人数为,
则第二小组的频数为
第三小组的频数为
第四小组的频数为
即第一、第二、第三、第四小组的频数分别为
易知将数据从小到大排列,第个数据在第三小组内,
所以学生跳绳次数的中位数落在第三小组内.
26. 分析:主视图、左视图、俯视图分别是从物体正面、左面和上面看所得到的图形.
解:如图所示.
27. 解:(1) 当a = 2, h = 3时,V = a2h = 12 ; S = 2a2+ 4ah =32.
(2) ∵ a2h = 12, 2a(a + 2h) =32,
∴ , a + 2h =,
∴ ===.
28. 分析:(1)把点B,C的坐标代入直线的解析式,解方程组即可得到直线的解析式;把点B,C,O的坐标代入抛物线的解析式,解方程组求出的值,即可得到抛物线的解析式.
(2)先根据抛物线的解析式求出点N的坐标,再根据三角形的面积公式可知,点P为抛物线的顶点时△PON底边ON上的高最大,面积最大,求出点P的纵坐标,代入面积公式即可得解.
(3)先求出点A,D的坐标,再设点P的坐标为(,),根据三角形的面积公式列式得到关于的一元二次方程,然后求出方程的解,再根据点P在轴的上方进行判断.
解:(1)根据题意,得解得
∴ 直线的解析式是.
根据图象,抛物线经过点B(1,3),C(2,2),O(0,0),
∴ 解得
∴ 抛物线的解析式是=.
(2)当时,,解得=0,=,∴ 点N的坐标是(,0).
∵ 点P的纵坐标越大,△PON的面积越大,
∴ 当点P是抛物线的顶点时,△PON的面积最大,
此时点P的纵坐标是 = = ,
=××=.
(3)不存在.理由如下:
由(1)知直线的解析式是
当=0时,=4;
当=0时,-+4=0,解得=4.
∴ 点A,D的坐标分别是A(0,4),D(4,0).
设点P的坐标是(,),则
×4=××4×(),
整理得=0,解得 =0,=-2,
此时点P不在轴的上方,不符合题意,
∴ 不存在点P,使得△POA的面积等于△POD面积的.
D
C
B
A
第11题图
D
C
B
A
开始
红 红 黄 蓝
红 红 黄 蓝
红 红 黄 蓝
红 红 黄 蓝
红 红 黄 蓝
第2次
第1次
第26题答图
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
期末检测题
(本检测题满分:120分,时间:120分钟)
一、选择题(每小题3分,共36分)
1. 若在函数中,随的增大而增大,且,则它的图象大致是( )
2.直线交坐标轴于两点,则不等式的解集
为( )
A. B. C. D.
3. 设点A(x1,y1)和B(x2,y2)是反比例函数y=图象上的两个点,当x1<x2<0时,y1<y2,则一次函数y=-2x+k的图象不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.对于函数,下列结论错误的是( )
A.当时,随的增大而增大
B.当时,随的增大而增大
C.时的函数值大于时的函数值
D.在函数图象所在的每个象限内,随的增大而增大
5. 如果关于x的一元二次方程kx2-2x-1=0有两个不相等的实数根,那么实数k的取值范围 是( )
A.k>-1 B.k<1且k≠0
C.k≥-1且k≠0 D.k>-1且k≠0
6. 已知一个直角三角形的两条直角边长恰好是方程的两个根,则这个直角三角形的斜边长是( )
A. B.3 C.6 D.9
7. 有五张卡片(形状、大小、质地都相同),上面分别画有下列图形:①线段;②正三角形;③平行四边形;④等腰梯形;⑤圆.将卡片背面朝上洗匀,从中任意抽取一张,正面图形一定满足既是轴对称图形又是中心对称图形的概率是( )
A. B. C. D.
8. 一个不透明的口袋里装有除颜色外都相同的5个白球和若干个红球,在不允许将球倒出来数的前提下,小亮为了估计其中的红球数,采用如下方法:先将口袋中的球摇匀,再从口袋里随机摸出一球,记下颜色,然后把它放回口袋中.不断重复上述过程.小亮共摸了100次,其中有10次摸到白球.因此小亮估计口袋中的红球大约有( )个.
A.45 B.48 C.50 D.55
9.如图所示,已知扇形的半径为,圆心角的度数为120°,若将此扇形围成一个圆锥,则围成的圆锥的侧面积为( )
A. B. C. D.
10. 如图所示,下列几何体中主视图、左视图、俯视图都相同的是( )
11.如图,在矩形ABCD中,AB=4 ,AD=2 ,动点M自点A出发沿A→B的方向以1 cm/s的速度运动,同时动点N自点A出发沿A→D→C的方向以2 cm/s的速度运动,当点N到达点C时,两点同时停止运动,设运动时间为(s),△AMN的面积为y(cm 2),则下列图象中能反映与之间的函数关系的是( )
12.某学校为了了解九年级学生的体能情况,随机选取30名学生测试一分钟仰卧起坐次数,并绘制了如图所示的直方图,学生仰卧起坐次数在25~30之间的频率为( )
A. B. C. D.
二、填空题(每小题3分,共24分)
13. 把抛物线的图象向右平移3个单位长度,再向下平移2个单位长度,所得图象的解析式为,则的值为 .
14. 如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸(单位:),计算出这个立体图形的表面积是200 .
15. 已知反比例函数的图象与经过原点的直线相交于两点,其中点的坐标为,那么点的坐标为 .
16. 如图所示,一个圆形转盘被等分成五个扇形区域,上面分别标有数字,转盘指针的位置固定,转动转盘后任其自由停止.转动转盘一次,当转盘停止转动时,记指针指向标有偶数所在区域的概率为(偶数),指针指向标有奇数所在区域的概率为 (奇数),则(偶数)_______(奇数)(填“”“”或“”).
17.有长度为的四条线段,从中任取三条线段能组成三角形的概率是________.
18. 如图所示,圆柱底面半径为2 cm,高为9π cm,点分别是圆柱两底面圆周上的点,且点,在同一母线上,用一棉线从点顺着圆柱侧面绕3圈到点,则棉线最短 为 cm.
19. 一个几何体的三视图如图所示,其中主视图和左视图都是腰长为4,底边长为2的等腰三角形,则这个几何体侧面展开图的面积为________.
20. 在同一平面内,下列4个函数:①②;③;④的图象不可能由函数的图象通过平移变换得到的是 .
三、解答题(共60分)
21. (7分)如图所示,已知反比例函数y1=的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
(1)求这两个函数的表达式;
(2)观察图象,当x>0时,直接写出y1>y2时自变量x的取值范围;
(3)如果点C与点A关于x轴对称,求△ABC的面积.
22. (7分)在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球,它们除颜色外完全相同,其中红球有2个,黄球有1个,蓝球有1个.现有一张电影票,小明和小亮决定通过摸球游戏定输赢(赢的一方获得电影票).游戏规则是:两人各摸1次球,先由小明从纸箱里随机摸出1个球,记录颜色后放回,将小球摇匀,再由小亮随机摸出1个球并记录颜色.若两人摸到的球颜色相同,则小明赢,否则小亮赢.这个游戏规则对双方公平吗?请你利用树状图或列表法说明理由.
23. (7分)在△ABC中,AB = ,AC = ,BC = 1.
(1)求证:∠A≠30°;
(2)将△ABC绕BC所在直线旋转一周,求所得几何体的表面积.
24. (7分)为了预防流感,某学校在休息日用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为(为常数).如图所示,根据图中提供的信息,解答下列问题:
(1)写出从药物释放开始,y与t之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米含药量降低到0.25毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?
25. (7分)为了了解小学生的体能情况,抽取了某小学同年级部分学生进行跳绳测试,将所得的数据整理后画出频数分布直方图,已知图中从左到右的前三个小组的频率分别是0.1,0.3,0.4,第一小组的频数是5.
(1)求第四小组的频率和参加这次测试的学生人数;
(2)在这次测试中,学生跳绳次数的中位数落在第几小组内?
26.(7分) 作出图中立体图形的三视图.
27.(8分)已知直四棱柱的底面是边长为a的正方形, 高为, 体积为V, 表面积为S.
(1) 当a = 2, h = 3时,分别求V和S;
(2) 当V = 12,S = 32时,求的值.
28.(10分)如图所示,抛物线经过原点O,与轴交于另一点N,直线与两坐标轴分别交于A,D两点,与抛物线交于B(1,3),C(2,2)两点.
(1)求直线与抛物线的解析式.
(2)若抛物线在轴上方的部分有一动点 P(,),求△PON面积的最大值.
(3)若动点P保持(2)中的运动路线,问是否存在点P,使得△POA的面积等于△POD面积的?若存在,请求出点P的坐标;若不存在,请说明理由.
期末检测题参考答案
1.B 解析:由随的增大而增大,知函数的图象由左至右上升,故k>0;又由,知函数的图象与轴的负半轴相交.
2.A 解析:由直线交坐标轴于两点,
知所以
解,得
3. A 解析:本题考查了反比例函数、一次函数的图象和性质.对于反比例函数,∵ x1<x2<0时,y1<y2,说明在同一个象限内,y随x的增大而增大,∴ k<0.∴ 一次函数y=-2x+k的图象与y轴交于负半轴,其图象经过第二、三、四象限,不经过第一象限.
4.C 解析:A.当时,的图象位于第四象限,随的增大而增大,正确;
B.当时,的图象位于第二象限,随的增大而增大,正确;
C.时的函数值为,时的函数值为,故时的函数值小于时的函数值,错误;
D.根据A,B可知,正确.
5. D 解析:∵ 一元二次方程kx2-2x-1=0有两个不相等的实数根,∴ Δ=b2-4ac=4+4k>0,且k≠0,解得k>-1且k≠0.
点拨:此题考查了一元二次方程根的判别式,根的判别式的值大于0,方程有两个不相等的实数根;根的判别式的值等于0,方程有两个相等的实数根;根的判别式的值小于0,方程没有实数根.本题在求k的取值范围时要注意二次项系数不为0的条件.
6. B 解析1:∵
∴ x==,∴ =+
∴ 这个直角三角形的斜边长是3,故选B.
解析2:设和是方程的两个根,
由一元二次方程根与系数的关系可得
∴ ,
∴ 这个直角三角形的斜边长是3,故选B.
7. B 解析:既是轴对称图形又是中心对称图形的有线段、圆,共2张,所以所求概率为.
8. A 解析:本题考查了简单随机事件的概率计算,设口袋中有x个红球,由题意得,P(摸到白球)==,解得x=45.
9. D 解析: .
10. C 解析:A.此半球的三视图分别为半圆拱形、半圆拱形、圆,不符合题意;
B.圆柱的三视图分别为长方形、长方形、圆,不符合题意;
C.球的三视图都是圆,符合题意;
D.六棱柱的三视图不相同,不符合题意.
故选C.
11. D 解析:在矩形ABCD中,AB =4 ,AD =2 cm,
AD +DC =AB +AD = 4+2= 6(cm).
∵ 点M以1 cm/s的速度运动,∴ 4÷1=4(s).
∵ 点N以2 cm/s的速度运动,∴ 6÷2=3(s),
∴ 点N先到达终点,运动时间为3 s.
①点N在AD上运动时,=AM AN= 2=(0≤≤1);
②点N在DC上运动时,=AM AD= 2= (1≤3).
∴ 能反映与之间的函数关系的是选项D.故选D.
12. D 解析:因为学生仰卧起坐次数在25~30之间的人数为12,所以学生仰卧起坐次数在25~30之间的频率为,故选D.
13. 解析:∵ =,
∴ 抛物线顶点坐标为(1,2).
依题意,得平移前抛物线顶点坐标为(-2,4),
∵ 平移不改变二次项系数,
∴ ,
比较系数,得.
14. 200 解析:根据三视图可得:上面的长方体长4 mm,高4 mm,宽2 mm,下面的长方体底面两边长分别为6 mm,8 mm,高为2 mm,∴ 立体图形的表面积是(mm 2).
15.(-2,-1) 解析:设直线的解析式为,因为直线和反比例函数的图象都经过点,将点的坐标代入可得,,故直线的解析式为,反比例函数的解析式为,联立可解得点的坐标为(-2,-1).
16. 解析:因为 , ,所以.
17. 解析:从长度为的四条线段中任取三条有四种情况: .
其中不能组成三角形,故从中任取三条线段能组成三角形的概率是.
18. 15π 解析:要求圆柱体侧面上两点之间的最短路径,最直 接的作法,就是将圆柱体侧面展开,然后利用两点之间线段最短解答.圆柱体侧面的展开图如图所示:用一棉线从点A顺着圆柱侧面绕3圈到点B的最短路径是:AC→CD→DB,即在圆柱体的侧面展开图长方形中,将长方形平均分成3个小长方形,点A沿着3个小长方形的对角线运动到点B的路线最短.
∵ 圆柱底面半径为2 cm,
∴ 长方形的宽即圆柱体的底面圆周长是2π×2=4π(cm).
又∵ 圆柱高为9π cm,∴ 小长方形的一条边长是3π cm.
根据勾股定理求得AC=CD=DB=5π cm,
∴ AC+CD+DB=15π cm.
19. 4π 解析:由几何体的主视图和左视图都是等腰三角形,
俯视图是带圆心的圆,可以判断这个几何体是圆锥.
依题意知母线长l=4,底面半径r=1,
则由圆锥的侧面积公式得S=πrl=π×1×4=4π.
20. ③④ 解析:能通过平移变换互相得到的二次函数的图象,其解析式的二次项系数相同.二次项的系数不是2的函数有③④.
21. 分析:(1)先把点A(1,4)的坐标代入y1=,求出k的值;再把点B(m,-2)的坐标代入y1=,求出m的值;最后把A,B两点的坐标分别代入y2=ax+b,组成关于a,b的二元一次方程组,解方程组求出a,b即可.(2)由图象可以看出,当0<x<1时,y1所对应的图象在y2所对应图象的上方.(3)由题意,得AC=8,点B到AC的距离是点B的横坐标与点A的横坐标之差的绝对值,即等于3,所以S△ABC=×8×3=12.
解:(1)∵ 点A(1,4)在y1=的图象上,
∴ k=1×4=4,∴ y1=.
∵ 点B在y1=的图象上,
∴ m=-2,
∴ 点B(-2,-2).
又∵ 点A,B在一次函数y2=ax+b的图象上,
∴ 解得 ∴ y2=2x+2.
∴ 这两个函数的表达式分别为y1=,y2=2x+2.
(2)由图象可知,当x>0,y1>y2时,自变量x的取值范围为0<x<1.
(3)∵ 点C与点A关于x轴对称,∴ C(1,-4).
如图所示,过点B作BD⊥AC,垂足为D,则D(1,-2),
于是△ABC的高BD=|1-(-2)|=3,底边AC=|4-(-4)|=8 .
∴ S△ABC=AC·BD=×8×3=12.
点拨:两个函数图象交点处的函数值相等,在交点的同侧,函数图象越高,函数值就越大.
22. 解:游戏规则对双方不公平.理由如下:
树状图如图所示.
第22题答图
或列表为:
红 红 黄 蓝
红 (红,红) (红,红) (红,黄) (红,蓝)
红 (红,红) (红,红) (红,黄) (红,蓝)
黄 (黄,红) (黄,红) (黄,黄) (黄,蓝)
蓝 (蓝,红) (蓝,红) (蓝,黄) (蓝,蓝)
由上述树状图或表格知:所有出现的等可能结果共有16种.
∴ P(小明赢)=,P(小亮赢)=错误!未指定书签。.
∴ 此游戏对双方不公平,小亮赢的可能性大.
23. 分析:(1)根据勾股定理的逆定理得到△ABC是直角三角形,且∠C为直角,利用三角函数计算出sin A,然后与sin 30°进行比较即可判断∠A≠30°;
(2)将△ABC绕BC所在直线旋转一周,所得的几何体为圆锥,圆锥的底面圆的半径为AC,母线长为AB,所得几何体的表面积分为底面积和侧面积,分别根据圆的面积公式和扇形的面积公式进行计算即可.
(1)证明:∵ BC2+AC2=1+2=3=AB2,
∴ △ABC是直角三角形,且∠C为直角.
∵ 30°,
∴ ∠A≠30°.
(2)解:将△ABC绕BC所在直线旋转一周,所得的几何体为圆锥,
∴ 圆锥的底面圆的半径=,
∴ 圆锥的底面圆的周长=2π =2π,母线长为,
∴ 几何体的表面积= 2π +π =(+2)π.
24.解: (1) 将点的坐标代入函数关系式, 解得, 有.
将代入, 得, 所以所求反比例函数关系式为;
再将点的坐标代入, 得,
所以所求正比例函数关系式为.
(2) 解不等式 , 解得 ,所以至少需要经过6小时后,学生才能进入教室.
25. 解:(1)由题意知,前三个小组的频率分别是
则第四小组的频率为
又由第一小组的频数为,其频率为,
所以参加这次测试的学生人数为
(2)由可得,参加测试的人数为,
则第二小组的频数为
第三小组的频数为
第四小组的频数为
即第一、第二、第三、第四小组的频数分别为
易知将数据从小到大排列,第个数据在第三小组内,
所以学生跳绳次数的中位数落在第三小组内.
26. 分析:主视图、左视图、俯视图分别是从物体正面、左面和上面看所得到的图形.
解:如图所示.
27. 解:(1) 当a = 2, h = 3时,V = a2h = 12 ; S = 2a2+ 4ah =32.
(2) ∵ a2h = 12, 2a(a + 2h) =32,
∴ , a + 2h =,
∴ ===.
28. 分析:(1)把点B,C的坐标代入直线的解析式,解方程组即可得到直线的解析式;把点B,C,O的坐标代入抛物线的解析式,解方程组求出的值,即可得到抛物线的解析式.
(2)先根据抛物线的解析式求出点N的坐标,再根据三角形的面积公式可知,点P为抛物线的顶点时△PON底边ON上的高最大,面积最大,求出点P的纵坐标,代入面积公式即可得解.
(3)先求出点A,D的坐标,再设点P的坐标为(,),根据三角形的面积公式列式得到关于的一元二次方程,然后求出方程的解,再根据点P在轴的上方进行判断.
解:(1)根据题意,得解得
∴ 直线的解析式是.
根据图象,抛物线经过点B(1,3),C(2,2),O(0,0),
∴ 解得
∴ 抛物线的解析式是=.
(2)当时,,解得=0,=,∴ 点N的坐标是(,0).
∵ 点P的纵坐标越大,△PON的面积越大,
∴ 当点P是抛物线的顶点时,△PON的面积最大,
此时点P的纵坐标是 = = ,
=××=.
(3)不存在.理由如下:
由(1)知直线的解析式是
当=0时,=4;
当=0时,-+4=0,解得=4.
∴ 点A,D的坐标分别是A(0,4),D(4,0).
设点P的坐标是(,),则
×4=××4×(),
整理得=0,解得 =0,=-2,
此时点P不在轴的上方,不符合题意,
∴ 不存在点P,使得△POA的面积等于△POD面积的.
D
C
B
A
第11题图
D
C
B
A
开始
红 红 黄 蓝
红 红 黄 蓝
红 红 黄 蓝
红 红 黄 蓝
红 红 黄 蓝
第2次
第1次
第26题答图
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
