第三章 函数的概念与性质 单元测试卷(含解析)
文档属性
| 名称 | 第三章 函数的概念与性质 单元测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 448.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 14:08:26 | ||
图片预览




文档简介
函数的概念与性质测试(时间:120分钟 满分:150分)
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知函数的值域是,则实数的取值范围是( )
A. B.
C. D.
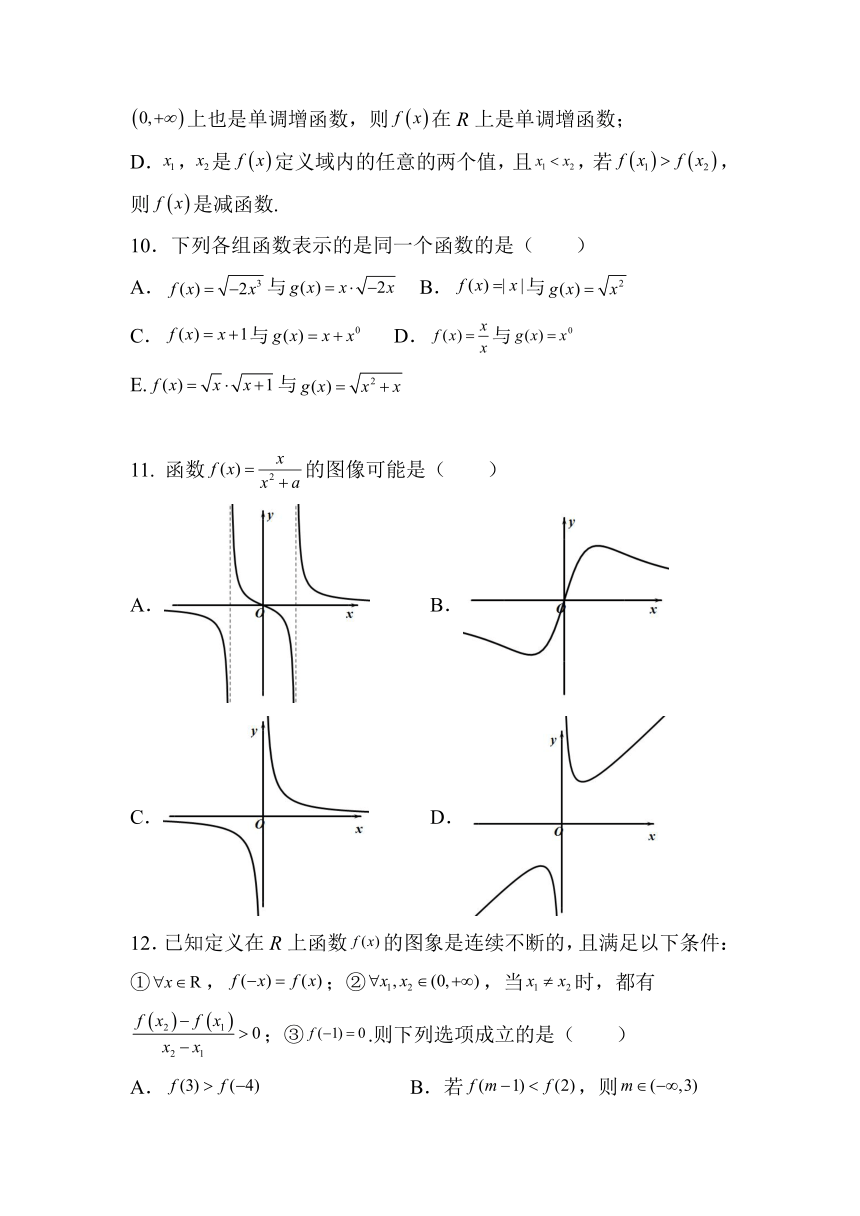
2.函数的图象大致为( )
A. B.
C. D.
3.若函数|在区间上不是单调函数,则实数的取值范围是( )
A. B.
C. D.
4.若函数单调递增,则实数a的取值范围是( )
A. B. C. D.
5.下列函数中,是偶函数,且在区间上为增函数的是( )
A. B.
C. D.
6.已知,若,则等于( )
A. B. C. D.
7. “龟兔赛跑”讲述了这样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉.当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点.用,分别表示乌龟和兔子所行的路程(t为时间),则下图与故事情节相吻合的是 ( )
A. B. C. D.
8.已知函数的图象关于直线对称,当时,恒成立,则满足的的取值范围是( )
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,有选错的得0分,部分选对的得2分。
9.给出下列命题,其中是错误命题的是( )
A.若函数的定义域为,则函数的定义域为;
B.函数的单调递减区间是;
C.若定义在R上的函数在区间上是单调增函数,在区间上也是单调增函数,则在R上是单调增函数;
D.,是定义域内的任意的两个值,且,若,则是减函数.
10.下列各组函数表示的是同一个函数的是( )
A.与 B.与
C.与 D.与
E.与
11. 函数的图像可能是( )
A. B.
C. D.
12.已知定义在R上函数的图象是连续不断的,且满足以下条件:①,;②,当时,都有;③.则下列选项成立的是( )
A. B.若,则
C.若, D.,,使得
三、填空题:本题共4小题,每小题5分,共20分。把答案填在题中横线上。
13.已知函数是幂函数,且在上单调递增,则实数________.
14.已知函数f(x)=则f(f(-4))=________.
15.函数y的定义域是 .
16.为满足人民对美好生活的向往,环保部门要求相关企业加强污水治理,排放未达标的企业要限期整改.设企业的污水排放量W与时间t的关系为W=f(t),用的大小评价在[a,b]这段时间内企业污水治理能力的强弱.已知整改期内,甲、乙两企业的污水排放量与时间的关系如图所示.
给出下列四个结论:
①在[t1,t2]这段时间内,甲企业的污水治理能力比乙企业强;
②在t2时刻,甲企业的污水治理能力比乙企业强;
③在t3时刻,甲,乙两企业的污水排放都已达标;
④甲企业在[0,t1],[t1,t2],[t2,t3]这三段时间中,在[0,t1]的污水治理能力最强.
其中所有正确结论的序号是 .
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分10分)
已知函数
(1)试判断函数在(-1,+)上的单调性,并给予证明;
(2)试判断函数在的最大值和最小值
18.(本小题满分12分)
设函数f(x)=x2-2|x|-1(-3≤x≤3).
(1)证明:函数f(x)是偶函数;
(2)画出这个函数的图象;
(3)指出函数f(x)的单调区间,并说明在各个单调区间上f(x)的单调性;
(4)求函数的值域.
19.(本小题满分12分)
已知幂函数f(x)=(m2-5m+7)·xm-1为偶函数.
(1)求f(x)的解析式;
(2)若g(x)=f(x)-ax-3在[1,3]上不是单调函数,求实数a的取值范围.
20.(本小题满分12分)
已知函数f(x)=x,且此函数图象过点(1,2).
(1)求实数m的值;
(2)判断函数f(x)的奇偶性并证明;
(3)讨论函数f(x)在(0,1)上的单调性,并证明你的结论.
21.(本小题满分12分)
已知A,B两城市相距100 km,在两地之间距离A城市x km的D处修建一垃圾处理厂来解决A,B两城市的生活垃圾和工业垃圾.为保证不影响两城市的环境,垃圾处理厂与市区距离不得少于10 km.已知垃圾处理费用和距离的平方与垃圾量之积的和成正比,比例系数为0.25.若A城市每天产生的垃圾量为20 t,B城市每天产生的垃圾量为10 t.
(1)求x的取值范围;
(2)把每天的垃圾处理费用y表示成x的函数;
(3)垃圾处理厂建在距离A城市多远处,才能使每天的垃圾处理费用最少?
22.(本小题满分12分)
已知函数.
(1)设,根据函数单调性的定义证明在区间上单调递增;
(2)当时,解关于x的不等式.
参考答案
1【解析】
二次函数的图象是开口向下的抛物线.
最大值为,且在时取得,而当或时,.
结合函数图象可知的取值范围是.
故选:C.
2【解析】
由函数的解析式可得:,则函数为奇函数,其图象关于坐标原点对称,选项CD错误;
当时,,选项B错误.
故选:A.
3【解析】
,分三种情况讨论.
当时,,所以;
当时,,在上显然单调;
当时,,所以.
综上:或.
故选B.
4【解析】
当时,函数单调递增
所以,解得
当时,是单调递增函数,
所以,
当时,一次函数取值要小于或等于指数式的值,
所以,
解之得:,
综上所述:实数a的取值范围是
故选:B
5【解析】
选项B中,函数不具备奇偶性,选项C中,函数是奇函数,
选项A,D中的函数是偶函数,但函数在区间上单调递减,故选A.
6【解析】
因为,所以,
所以即,选D.
7【解析】
由题意可得的始终是匀速增长,开始时,的增长比较快,但中间有一段时间停止增长,在最后一段时间里,的增长又较快,但的值没有超过的值,
结合所给的图象可知,B选项适合,故选B.
8【解析】
当时,恒成立,
所以恒成立,即函数在上单调递增,
又因为函数的图象关于直线对称,所以在上单调递减,
若要满足,即,解得,
故选A.
9【解析】
对于A,若函数的定义域为,
则函数的定义域为,故A错误;
对于B,函数的单调递减区间是和,故B错误;
对于C,若定义在上的函数在区间上是单调增函数,
在区间上也是单调增函数,则在上不一定为单调增函数,故C错误;
对于D,为单调性的定义,正确.故答案为:ABC.
10【解析】
对于A:与的对应关系不同,故与表的不是同一个函数;
对于B:与的定义域和对应关系均相同,故与表示的是同一个函数;
对于C:的定义域为R,的定义域为,故与表示的不是同一个函数;
对于D:与的对应关系和定义域均相同,故与表示的是同一个函数;
对于E:的定义域是,的定义域是,故与表示的不是同一个函数.故选BD.
11【解析】
由题可知,函数,
若,则,选项C可能;
若,则函数定义域为,且,选项B可能;
若,则,选项A可能,
故不可能是选项D,
故选:ABC.
12【解析】
由条件①得是偶函数,条件②得在上单调递增
所以,故A错
若,则,得,故B错
若则或,因为
所以或,故C正确
因为定义在R上函数的图象是连续不断的,且在上单调递增
所以,所以对,只需即可,故D正确
故选:CD
13【解析】
∵幂函数f(x)=(m2﹣m﹣1)xm在区间(0,+∞)上单调递增,
∴,解得m=2或-1(舍).故答案为2.
14【解析】
由题得,
所以f(f(-4))=.
故答案为:-2
15【解析】
由7+6x﹣x2≥0,得x2﹣6x﹣7≤0,解得:﹣1≤x≤7.
∴函数y的定义域是[﹣1,7].故答案为:[﹣1,7].
16【解析】
设甲企业的污水排放量W与时间t的关系为W=f(t),乙企业的污水排放量W与时间t的关系为W=g(t).
对于①,在[t1,t2]这段时间内,甲企业的污水治理能力为,
乙企业的污水治理能力为.
由图可知,f(t1)﹣f(t2)>g(t1)﹣g(t2),∴,
即甲企业的污水治理能力比乙企业强,故①正确;
对于②,由图可知,f(t)在t2时刻的切线的斜率小于g(t)在t2时刻的切线的斜率,但两切线斜率均为负值,
∴在t2时刻,甲企业的污水治理能力比乙企业强,故②正确;
对于③,在t3时刻,甲,乙两企业的污水排放都小于污水达标排放量,
∴在t3时刻,甲,乙两企业的污水排放都已达标,故③正确;
对于④,由图可知,甲企业在[0,t1],[t1,t2],[t2,t3]这三段时间中,在[t1,t2]的污水治理能力最强,故④错误.
∴正确结论的序号是①②③.
故答案为:①②③.
17【解析】
(1)∵,
∴函数在上是增函数,
证明:任取,,且,
则,
∵,∴,,
∴,即,
∴在上是增函数.
(2)∵在上是增函数,
∴在上单调递增,
它的最大值是,
最小值是.
18【解析】
(1)证明:∵函数f(x)的定义域关于原点对称,
且f(-x)=(-x)2-2|-x|-1
=x2-2|x|-1=f(x),
即f(-x)=f(x),∴f(x)是偶函数.
(2)当0≤x≤3时,
f(x)=x2-2x-1=(x-1)2-2.
当-3≤x<0时,f(x)=x2+2x-1=(x+1)2-2.
即f(x)=
根据二次函数的作图方法,可得函数图象如下图.
(3)函数f(x)的单调区间为[-3,-1),[-1,0),[0,1),[1,3].
f(x)在区间[-3,-1)和[0,1)上单调递减,
在[-1,0)和[1,3]上单调递增.
(4)当0≤x≤3时,函数f(x)=(x-1)2-2的最小值为-2,最大值为f(3)=2;
当-3≤x<0时,函数f(x)=(x+1)2-2的最小值为-2,最大值为f(-3)=2.故函数f(x)的值域为[-2,2].
19【解析】
(1)由题意得m2-5m+7=1,
即m2-5m+6=0,解得m=2或m=3.
又f(x)为偶函数,所以m=3,此时f(x)=x2.
(2)由(1)知,g(x)=x2-ax-3,因为g(x)=x2-ax-3在[1,3]上不是单调函数,所以1<<3,解得220【解析】
(1)∵函数f(x)=x,且此函数图象过点(1,2),
∴2=1+m,
∴m=1;
(2)f(x)=x,定义域为:,
又f(﹣x)=﹣xf(x),
∴函数f(x)是奇函数;
(3)函数f(x)在(0,1)上单调递减,
设0<x1<x2<1,
则,
∵0<x1<x2<1,
∴x1﹣x2<0,0<x1x2<1,x1x2﹣1<0,
∴,
即f(x1)>f(x2),
∴f(x)在(0,1)上的单调递减.
21【解析】
(1)由题意可得x≥10,100-x≥10.
所以10≤x≤90.
所以x的取值范围为[10,90].
(2)由题意,得y=0.25[20x2+10(100-x)2],
即y=x2-500x+25000(10≤x≤90).
(3)由y=x2-500x+25000=(10≤x≤90),则当x=时,y最小.即当垃圾处理厂建在距离A城市 km时,才能使每天的垃圾处理费用最少.
22【解析】
(1)由题意得,,且,
则.
由,得.于是,即
所以函数在区间上单调递增
(2)原不等式可化为.因为,故.
(i)当,即时,得或.
(ii)当,即时,得到,所以;
(iii)当,即时,得或.
综上所述,
当时,不等式的解集为;
当时,不等式的解集为;
当时,不等式的解集为
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知函数的值域是,则实数的取值范围是( )
A. B.
C. D.
2.函数的图象大致为( )
A. B.
C. D.
3.若函数|在区间上不是单调函数,则实数的取值范围是( )
A. B.
C. D.
4.若函数单调递增,则实数a的取值范围是( )
A. B. C. D.
5.下列函数中,是偶函数,且在区间上为增函数的是( )
A. B.
C. D.
6.已知,若,则等于( )
A. B. C. D.
7. “龟兔赛跑”讲述了这样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉.当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点.用,分别表示乌龟和兔子所行的路程(t为时间),则下图与故事情节相吻合的是 ( )
A. B. C. D.
8.已知函数的图象关于直线对称,当时,恒成立,则满足的的取值范围是( )
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,有选错的得0分,部分选对的得2分。
9.给出下列命题,其中是错误命题的是( )
A.若函数的定义域为,则函数的定义域为;
B.函数的单调递减区间是;
C.若定义在R上的函数在区间上是单调增函数,在区间上也是单调增函数,则在R上是单调增函数;
D.,是定义域内的任意的两个值,且,若,则是减函数.
10.下列各组函数表示的是同一个函数的是( )
A.与 B.与
C.与 D.与
E.与
11. 函数的图像可能是( )
A. B.
C. D.
12.已知定义在R上函数的图象是连续不断的,且满足以下条件:①,;②,当时,都有;③.则下列选项成立的是( )
A. B.若,则
C.若, D.,,使得
三、填空题:本题共4小题,每小题5分,共20分。把答案填在题中横线上。
13.已知函数是幂函数,且在上单调递增,则实数________.
14.已知函数f(x)=则f(f(-4))=________.
15.函数y的定义域是 .
16.为满足人民对美好生活的向往,环保部门要求相关企业加强污水治理,排放未达标的企业要限期整改.设企业的污水排放量W与时间t的关系为W=f(t),用的大小评价在[a,b]这段时间内企业污水治理能力的强弱.已知整改期内,甲、乙两企业的污水排放量与时间的关系如图所示.
给出下列四个结论:
①在[t1,t2]这段时间内,甲企业的污水治理能力比乙企业强;
②在t2时刻,甲企业的污水治理能力比乙企业强;
③在t3时刻,甲,乙两企业的污水排放都已达标;
④甲企业在[0,t1],[t1,t2],[t2,t3]这三段时间中,在[0,t1]的污水治理能力最强.
其中所有正确结论的序号是 .
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分10分)
已知函数
(1)试判断函数在(-1,+)上的单调性,并给予证明;
(2)试判断函数在的最大值和最小值
18.(本小题满分12分)
设函数f(x)=x2-2|x|-1(-3≤x≤3).
(1)证明:函数f(x)是偶函数;
(2)画出这个函数的图象;
(3)指出函数f(x)的单调区间,并说明在各个单调区间上f(x)的单调性;
(4)求函数的值域.
19.(本小题满分12分)
已知幂函数f(x)=(m2-5m+7)·xm-1为偶函数.
(1)求f(x)的解析式;
(2)若g(x)=f(x)-ax-3在[1,3]上不是单调函数,求实数a的取值范围.
20.(本小题满分12分)
已知函数f(x)=x,且此函数图象过点(1,2).
(1)求实数m的值;
(2)判断函数f(x)的奇偶性并证明;
(3)讨论函数f(x)在(0,1)上的单调性,并证明你的结论.
21.(本小题满分12分)
已知A,B两城市相距100 km,在两地之间距离A城市x km的D处修建一垃圾处理厂来解决A,B两城市的生活垃圾和工业垃圾.为保证不影响两城市的环境,垃圾处理厂与市区距离不得少于10 km.已知垃圾处理费用和距离的平方与垃圾量之积的和成正比,比例系数为0.25.若A城市每天产生的垃圾量为20 t,B城市每天产生的垃圾量为10 t.
(1)求x的取值范围;
(2)把每天的垃圾处理费用y表示成x的函数;
(3)垃圾处理厂建在距离A城市多远处,才能使每天的垃圾处理费用最少?
22.(本小题满分12分)
已知函数.
(1)设,根据函数单调性的定义证明在区间上单调递增;
(2)当时,解关于x的不等式.
参考答案
1【解析】
二次函数的图象是开口向下的抛物线.
最大值为,且在时取得,而当或时,.
结合函数图象可知的取值范围是.
故选:C.
2【解析】
由函数的解析式可得:,则函数为奇函数,其图象关于坐标原点对称,选项CD错误;
当时,,选项B错误.
故选:A.
3【解析】
,分三种情况讨论.
当时,,所以;
当时,,在上显然单调;
当时,,所以.
综上:或.
故选B.
4【解析】
当时,函数单调递增
所以,解得
当时,是单调递增函数,
所以,
当时,一次函数取值要小于或等于指数式的值,
所以,
解之得:,
综上所述:实数a的取值范围是
故选:B
5【解析】
选项B中,函数不具备奇偶性,选项C中,函数是奇函数,
选项A,D中的函数是偶函数,但函数在区间上单调递减,故选A.
6【解析】
因为,所以,
所以即,选D.
7【解析】
由题意可得的始终是匀速增长,开始时,的增长比较快,但中间有一段时间停止增长,在最后一段时间里,的增长又较快,但的值没有超过的值,
结合所给的图象可知,B选项适合,故选B.
8【解析】
当时,恒成立,
所以恒成立,即函数在上单调递增,
又因为函数的图象关于直线对称,所以在上单调递减,
若要满足,即,解得,
故选A.
9【解析】
对于A,若函数的定义域为,
则函数的定义域为,故A错误;
对于B,函数的单调递减区间是和,故B错误;
对于C,若定义在上的函数在区间上是单调增函数,
在区间上也是单调增函数,则在上不一定为单调增函数,故C错误;
对于D,为单调性的定义,正确.故答案为:ABC.
10【解析】
对于A:与的对应关系不同,故与表的不是同一个函数;
对于B:与的定义域和对应关系均相同,故与表示的是同一个函数;
对于C:的定义域为R,的定义域为,故与表示的不是同一个函数;
对于D:与的对应关系和定义域均相同,故与表示的是同一个函数;
对于E:的定义域是,的定义域是,故与表示的不是同一个函数.故选BD.
11【解析】
由题可知,函数,
若,则,选项C可能;
若,则函数定义域为,且,选项B可能;
若,则,选项A可能,
故不可能是选项D,
故选:ABC.
12【解析】
由条件①得是偶函数,条件②得在上单调递增
所以,故A错
若,则,得,故B错
若则或,因为
所以或,故C正确
因为定义在R上函数的图象是连续不断的,且在上单调递增
所以,所以对,只需即可,故D正确
故选:CD
13【解析】
∵幂函数f(x)=(m2﹣m﹣1)xm在区间(0,+∞)上单调递增,
∴,解得m=2或-1(舍).故答案为2.
14【解析】
由题得,
所以f(f(-4))=.
故答案为:-2
15【解析】
由7+6x﹣x2≥0,得x2﹣6x﹣7≤0,解得:﹣1≤x≤7.
∴函数y的定义域是[﹣1,7].故答案为:[﹣1,7].
16【解析】
设甲企业的污水排放量W与时间t的关系为W=f(t),乙企业的污水排放量W与时间t的关系为W=g(t).
对于①,在[t1,t2]这段时间内,甲企业的污水治理能力为,
乙企业的污水治理能力为.
由图可知,f(t1)﹣f(t2)>g(t1)﹣g(t2),∴,
即甲企业的污水治理能力比乙企业强,故①正确;
对于②,由图可知,f(t)在t2时刻的切线的斜率小于g(t)在t2时刻的切线的斜率,但两切线斜率均为负值,
∴在t2时刻,甲企业的污水治理能力比乙企业强,故②正确;
对于③,在t3时刻,甲,乙两企业的污水排放都小于污水达标排放量,
∴在t3时刻,甲,乙两企业的污水排放都已达标,故③正确;
对于④,由图可知,甲企业在[0,t1],[t1,t2],[t2,t3]这三段时间中,在[t1,t2]的污水治理能力最强,故④错误.
∴正确结论的序号是①②③.
故答案为:①②③.
17【解析】
(1)∵,
∴函数在上是增函数,
证明:任取,,且,
则,
∵,∴,,
∴,即,
∴在上是增函数.
(2)∵在上是增函数,
∴在上单调递增,
它的最大值是,
最小值是.
18【解析】
(1)证明:∵函数f(x)的定义域关于原点对称,
且f(-x)=(-x)2-2|-x|-1
=x2-2|x|-1=f(x),
即f(-x)=f(x),∴f(x)是偶函数.
(2)当0≤x≤3时,
f(x)=x2-2x-1=(x-1)2-2.
当-3≤x<0时,f(x)=x2+2x-1=(x+1)2-2.
即f(x)=
根据二次函数的作图方法,可得函数图象如下图.
(3)函数f(x)的单调区间为[-3,-1),[-1,0),[0,1),[1,3].
f(x)在区间[-3,-1)和[0,1)上单调递减,
在[-1,0)和[1,3]上单调递增.
(4)当0≤x≤3时,函数f(x)=(x-1)2-2的最小值为-2,最大值为f(3)=2;
当-3≤x<0时,函数f(x)=(x+1)2-2的最小值为-2,最大值为f(-3)=2.故函数f(x)的值域为[-2,2].
19【解析】
(1)由题意得m2-5m+7=1,
即m2-5m+6=0,解得m=2或m=3.
又f(x)为偶函数,所以m=3,此时f(x)=x2.
(2)由(1)知,g(x)=x2-ax-3,因为g(x)=x2-ax-3在[1,3]上不是单调函数,所以1<<3,解得2
(1)∵函数f(x)=x,且此函数图象过点(1,2),
∴2=1+m,
∴m=1;
(2)f(x)=x,定义域为:,
又f(﹣x)=﹣xf(x),
∴函数f(x)是奇函数;
(3)函数f(x)在(0,1)上单调递减,
设0<x1<x2<1,
则,
∵0<x1<x2<1,
∴x1﹣x2<0,0<x1x2<1,x1x2﹣1<0,
∴,
即f(x1)>f(x2),
∴f(x)在(0,1)上的单调递减.
21【解析】
(1)由题意可得x≥10,100-x≥10.
所以10≤x≤90.
所以x的取值范围为[10,90].
(2)由题意,得y=0.25[20x2+10(100-x)2],
即y=x2-500x+25000(10≤x≤90).
(3)由y=x2-500x+25000=(10≤x≤90),则当x=时,y最小.即当垃圾处理厂建在距离A城市 km时,才能使每天的垃圾处理费用最少.
22【解析】
(1)由题意得,,且,
则.
由,得.于是,即
所以函数在区间上单调递增
(2)原不等式可化为.因为,故.
(i)当,即时,得或.
(ii)当,即时,得到,所以;
(iii)当,即时,得或.
综上所述,
当时,不等式的解集为;
当时,不等式的解集为;
当时,不等式的解集为
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
