相似三角形的判定和性质复习2[下学期]
文档属性
| 名称 | 相似三角形的判定和性质复习2[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 468.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-19 22:49:00 | ||
图片预览



文档简介
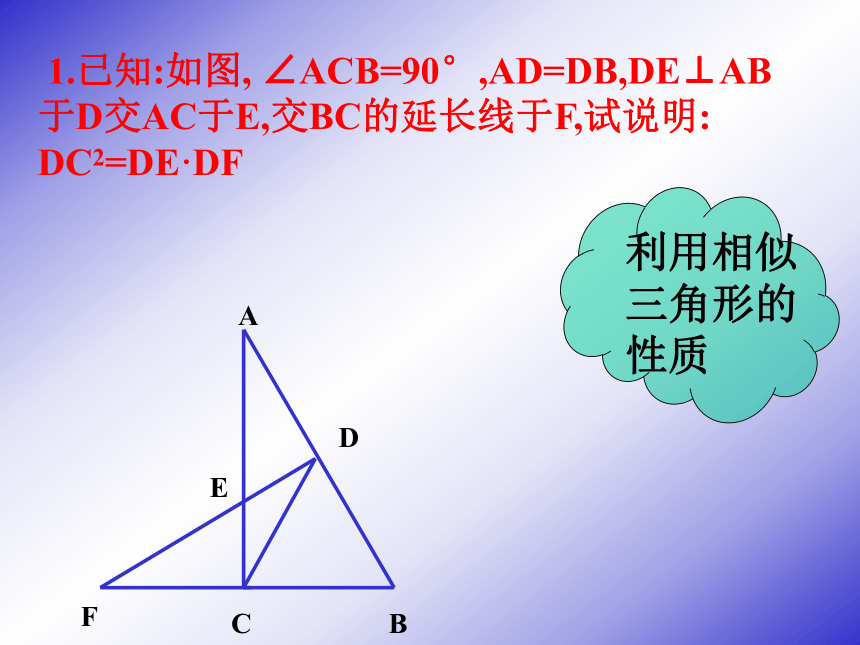
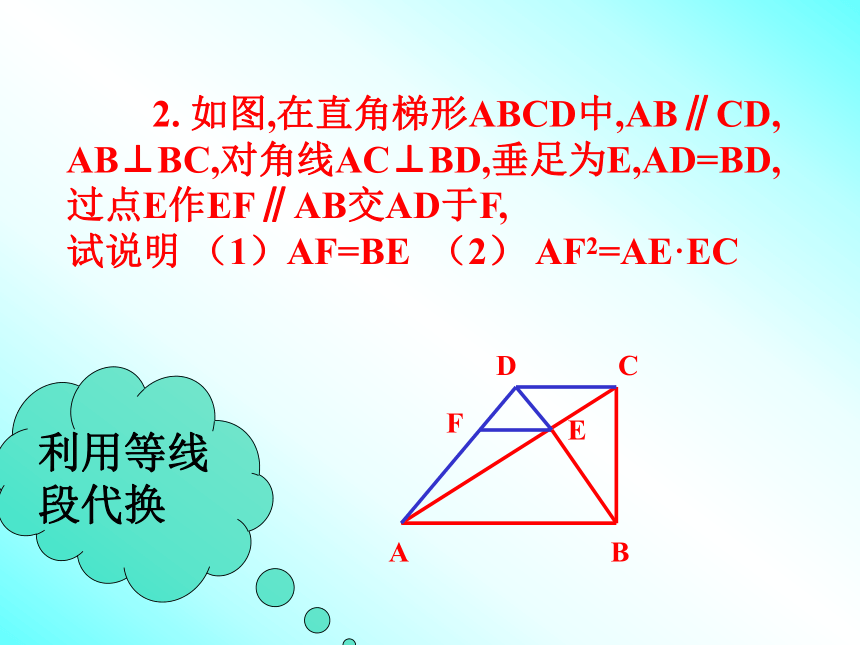
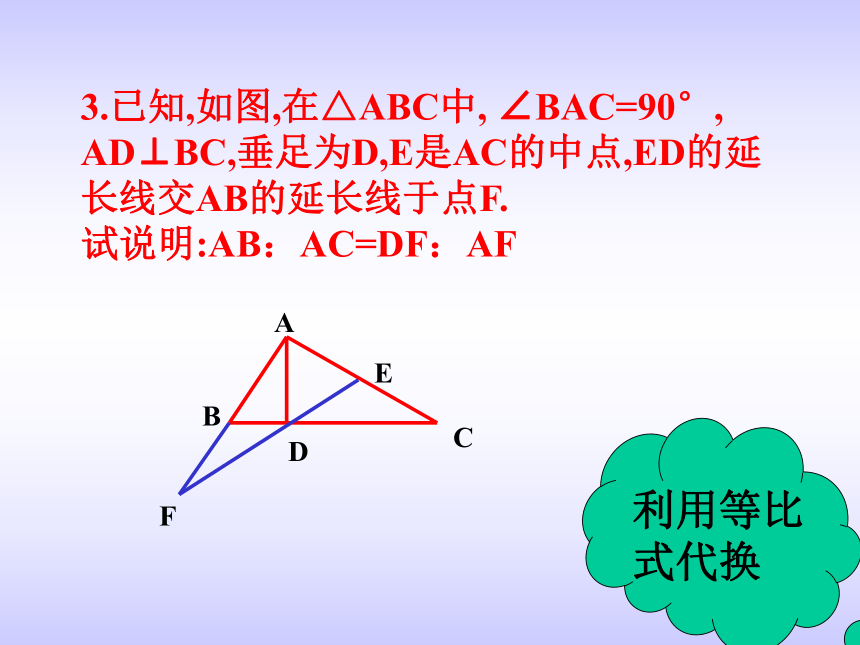
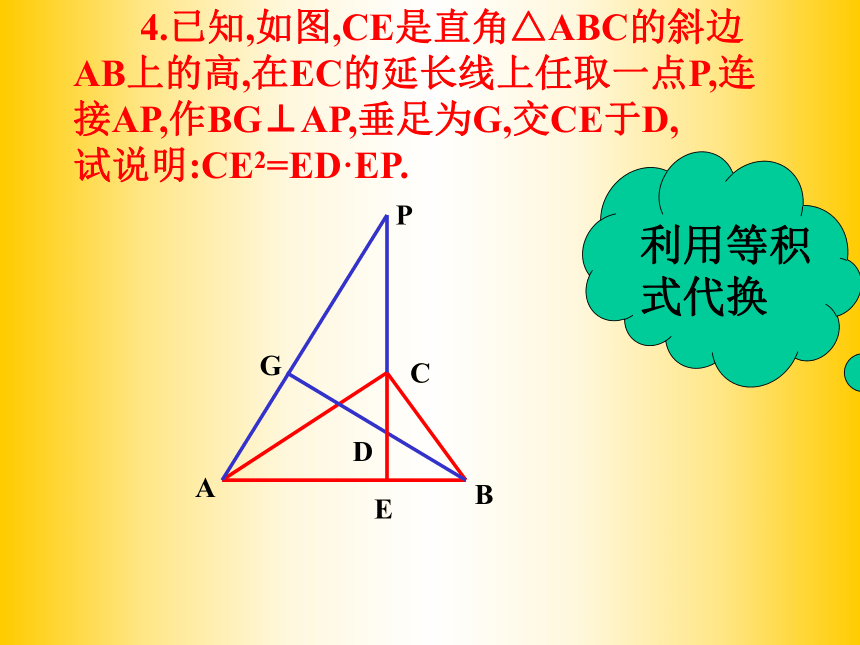
课件14张PPT。2 0 0 6. 0 4 .2 0.相似三角形复习(2)——比例式、等积式的几种常见证明方法许河中学 周美华合作探究 1.已知:如图, ∠ACB=90°,AD=DB,DE⊥AB于D交AC于E,交BC的延长线于F,试说明: DC2=DE·DF 利用相似三角形的性质ADBFCE 2. 如图,在直角梯形ABCD中,AB∥CD, AB⊥BC,对角线AC⊥BD,垂足为E,AD=BD,过点E作EF∥AB交AD于F, 试说明 (1)AF=BE (2) AF2=AE·EC利用等线段代换3.已知,如图,在△ABC中, ∠BAC=90°, AD⊥BC,垂足为D,E是AC的中点,ED的延长线交AB的延长线于点F. 试说明:AB:AC=DF:AF利用等比式代换 4.已知,如图,CE是直角△ABC的斜边AB上的高,在EC的延长线上任取一点P,连接AP,作BG⊥AP,垂足为G,交CE于D, 试说明:CE2=ED·EP.利用等积式代换协作交流BE2=EA·ECAC:AB=AD:BDEC2=EA·EB快速抢答在这一个图形中,有两个垂直,有____对相似,有___对互余的角,有_____组对应成比例的线段,它们分别是
三四五AC2=AD·AB
BC2=BD·AB
CD2=AD·BD
AC:AD=BC:CD
BC:BD=AC:CD牛刀小试 如上图, ∠BAC=120°, △ADE是等边三角形,小丽发现图中有些线段是其他两条线段的比例中项,你知道小丽说的是哪些线段吗? 它们分别是哪些线段的比例中项吗? 1.通过本节课的学习,你有什么收获?还有什么困惑吗?
2.你对自己本节课的表现满意吗?为什么?及时小结,自我评价作业: 作业纸老师寄语:若希望成功,当以恒心为良友,以经验为参谋,以信心为光荣,以希望为哨兵。再 见欢迎多提宝贵意见
三四五AC2=AD·AB
BC2=BD·AB
CD2=AD·BD
AC:AD=BC:CD
BC:BD=AC:CD牛刀小试 如上图, ∠BAC=120°, △ADE是等边三角形,小丽发现图中有些线段是其他两条线段的比例中项,你知道小丽说的是哪些线段吗? 它们分别是哪些线段的比例中项吗? 1.通过本节课的学习,你有什么收获?还有什么困惑吗?
2.你对自己本节课的表现满意吗?为什么?及时小结,自我评价作业: 作业纸老师寄语:若希望成功,当以恒心为良友,以经验为参谋,以信心为光荣,以希望为哨兵。再 见欢迎多提宝贵意见
