高中数学必修第一册人教A版(2019)5.4《正弦函数、余弦函数的性质---单调性和最值》名师课件(共28张PPT)
文档属性
| 名称 | 高中数学必修第一册人教A版(2019)5.4《正弦函数、余弦函数的性质---单调性和最值》名师课件(共28张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 18:42:53 | ||
图片预览





文档简介
(共28张PPT)
y
x
o
1
-1
y=sinx,x [0, 2 ]
y=cosx,x [0, 2 ]
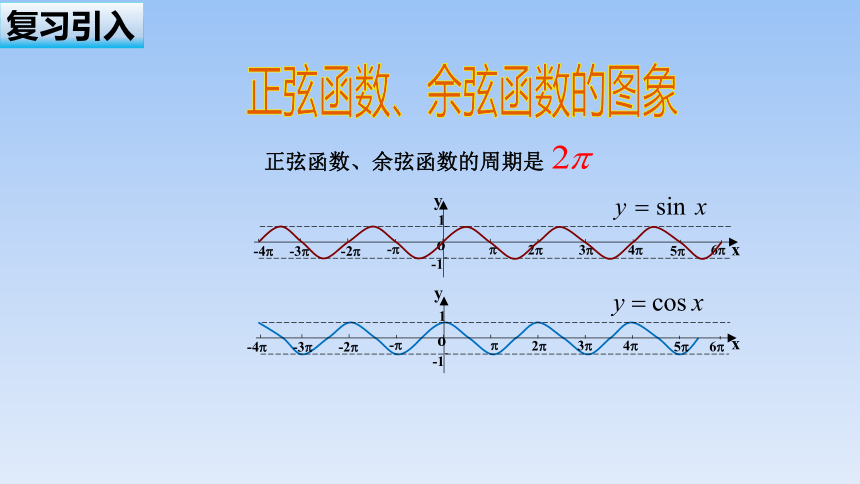
正弦函数、余弦函数的图象
复习引入
正弦函数、余弦函数的图象
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
x
6
o
-
-1
2
3
4
5
-2
-3
-4
1
y
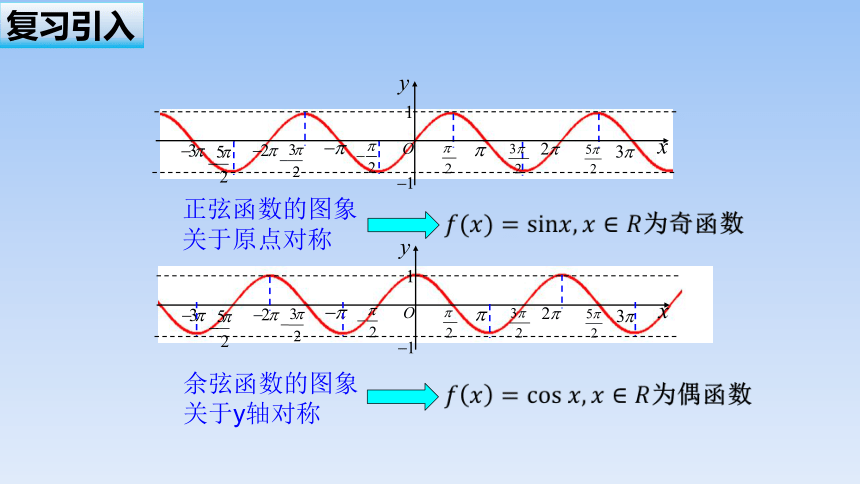
正弦函数、余弦函数的周期是
复习引入
正弦函数的图象关于原点对称
余弦函数的图象关于y轴对称
复习引入
人教A版同步教材名师课件
正弦函数、余弦函数的性质
---单调性和最值
学习目标
学 习 目 标 核心素养
掌握正弦函数、余弦函数的图象与性质 数学抽象
会求简单函数的定义域、值域、最小正周期和单调区间 逻辑推理
了解从特殊到一般,从一般到特殊的辩证思想方法和分析、探索、化归、类比的科学研究方法在解决数学问题中的应用 数学抽象
课程目标
1.了解周期函数与最小正周期的意义;
2.了解三角函数的周期性和奇偶性;
3.会利用周期性定义和诱导公式求简单三角函数的周期;
4.借助图象直观理解正、余弦函数在[0,2π]上的性质(单调性、最值、图象与x轴的交点等);
5.能利用性质解决一些简单问题.
数学学科素养
1.数学抽象:理解周期函数、周期、最小正周期等的含义;
2.逻辑推理: 求正弦、余弦形函数的单调区间;
3.数学运算:利用性质求周期、比较大小、最值、值域及判断奇偶性.
4.数学建模:让学生借助数形结合的思想,通过图像探究正、余弦函数的性质.
学习目标
正弦函数性质的研究
定义域:
R
值 域:
[ - 1, 1 ]
x
y
o
-
-1
2
3
4
-2
-3
1
探究新知
正弦函数性质的研究
x
y
o
-
-1
2
3
4
-2
-3
1
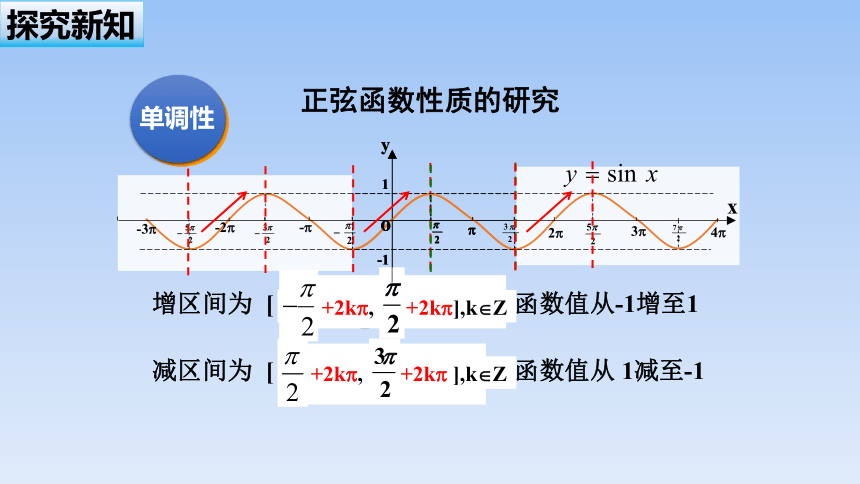
增区间为 [ , ] 函数值从-1增至1
减区间为 [ , ] 函数值从 1减至-1
+2k , +2k ],k Z
+2k , +2k ],k Z
x
y
o
-
-1
2
3
4
-2
-3
1
单调性
探究新知
正弦函数性质的研究
x
y
o
-
-1
2
3
4
-2
-3
1
x
y
o
-
-1
2
3
4
-2
-3
1
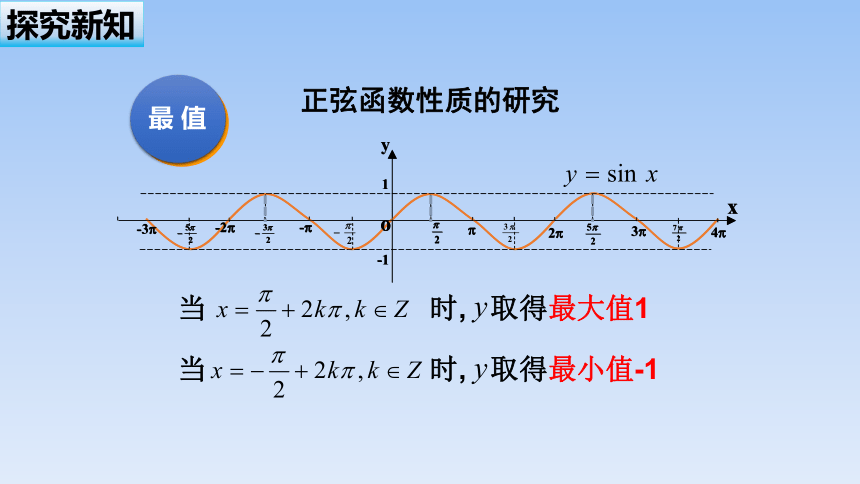
当 时, 取得最大值1
当 时, 取得最小值-1
最 值
探究新知
x
y
o
-
-1
2
3
4
-2
-3
1
正弦函数性质的研究
对称轴:
对称中心:
对称性
探究新知
定义域:
R
值 域:
[ - 1, 1 ]
增区间:
减区间:
奇偶性:
对称轴:
对称中心:
最 值:
y
x
o
-
-1
2
3
4
-2
-3
1
小组讨论:余弦函数的性质
探究新知
余弦函数性质的研究
例1、下列函数有最大值、最小值吗? 如果有,请写出取最大值、最小值时自变量的集合,并求出最大值、最小值.
(1), ∈R; (2), ∈R.
容易知道 , 这两个函数都有最大值 、 最小值 .
(1)使函数 , ∈R取得最大值的集合 , 就是使函数 , ∈R取得最大值的 的集合{∈Z};
使函数, ∈R , 取得最小值的的集合 , 就是使函数 , ∈R取得最小值的 的集合{∈Z}.
函数, ∈R 的最大值是 1=2; 最小值是 .
解析
典例讲解
例1、下列函数有最大值、最小值吗? 如果有,请写出取最大值、最小值时自变量的集合,并求出最大值、最小值.
(1), ∈R; (2), ∈R.
解析
(2) 令 z =2, 使函数 , z∈R 取得最大值的 z 的集合 , 就是使 ,z∈R 取得最小值的 z 的集合{z=+2kπ , k ∈Z}.
由 z=2=+2kπ ,得=+kπ . 所以 , 使函数 , ∈R取得最大值的 的集合是 =+kπ, k ∈Z}.
同理 , 使函数 , ∈R取得最小值的 的集合是{=+kπ, k ∈Z}.
函数 , ∈R的最大值是, 最小值是.
典例讲解
例2、利用三角函数的单调性,比较下列各组数的大小.
且在上递增,
,即
解析
典例讲解
利用诱导公式化到同一单调区间,再根据单调性比较大小;
首先化成同名三角函数,再把角化到同一单调区间,然后比较大小.
思路
解析
(3)利用函数的单调性比较大小.
比较三角函数值大小的步骤
(1)异名函数化为同名函数;
(2)利用诱导公式把角转化到同一单调区间上;
方法归纳
变式训练
1.
.
解析
,
,
上是减函数,
上是增函数,
例3、.
当是减函数时, 是增函数,
因为函数, 的单调递减区间为 ,所以令,所以函数的单调递增区间为
解析
典例讲解
,把看作一个整体,根据函数的单调性,列出关于的不等式,求解不等式,即可得到对应的单调区间.
思路
解析
方法归纳
求函数或(其中、、 为常数, ≠0,且≠0,∈)单调性的步骤
第一步 写出函数或为增函数或减函数时满足的不等式
第二步 将视为一个整体,代入到上述不等式
第三步 解第二步中的不等式,求出的范围
第四步 下结论
当三角函数中自变量的系数为负数时,要把系数转化为正数后,再求单调区间.
变式训练
2.
.
解析
令,即,
的单调递增区间是.
变式训练
2.
.
解析
函数的单调递增区间即为函数
例4、已知是正数,函数在区间,求的取值范围.
由
得
的单调递增区间是
根据题意,得,
从而有解得 故的取值范围是 .
解析
典例讲解
根据正弦函数的单调递增区间确定函数的单调递增区间,再根据函数在区间单调递增,建立不等式组,即可求得的取值范围.
思路
解析
方法归纳
已知函数(其中,, 为常数, >0, >0)的单调区间求或,一般将代入的相应的单调区间所对应的不等式,求出的范围,对应已知的单调区间建立关于或的不等式(组)进行求解.
变式训练
3.
A. B. C. D.
解析
由 , 得,
的单调递减区间是.
根据题意,得,
从而有解得故的取值范围是
(3)形如y=Asin(ωx+φ)(A>0,ω>0)的函数的最值通常利用“整体代换”,即令ωx+φ=z,将函数转化为y=Asin z的形式求最值.
正弦函数、余弦函数最值的释疑
(1)明确正、余弦函数的有界性,即|sin x|≤1,|cos x|≤1.
(2)对有些正、余弦函数,其最值不一定是1或-1,要依赖函数定义域来决定.
素养提炼
当堂练习
1.函数的最大值及取最大值时的值为( )
2.函数的最大值是( )
3·已知函数的图象关于直线对称,则可能是( )
A.
C
C
C
当堂练习
4.下列函数中,周期为,且在区间上为减函数的是( )
A. B.
C. D.
5.函数的单调递增区间为__________________.
6.函数的单调递增区间为_________________.
B
定义域
值 域
单调性 增区间
减区间
最值
奇偶性
对称轴
对称中心
R
R
[ - 1, 1 ]
[ - 1, 1 ]
偶函数
奇函数
归纳小结
作 业
P207练习:1、2、3
y
x
o
1
-1
y=sinx,x [0, 2 ]
y=cosx,x [0, 2 ]
正弦函数、余弦函数的图象
复习引入
正弦函数、余弦函数的图象
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
x
6
o
-
-1
2
3
4
5
-2
-3
-4
1
y
正弦函数、余弦函数的周期是
复习引入
正弦函数的图象关于原点对称
余弦函数的图象关于y轴对称
复习引入
人教A版同步教材名师课件
正弦函数、余弦函数的性质
---单调性和最值
学习目标
学 习 目 标 核心素养
掌握正弦函数、余弦函数的图象与性质 数学抽象
会求简单函数的定义域、值域、最小正周期和单调区间 逻辑推理
了解从特殊到一般,从一般到特殊的辩证思想方法和分析、探索、化归、类比的科学研究方法在解决数学问题中的应用 数学抽象
课程目标
1.了解周期函数与最小正周期的意义;
2.了解三角函数的周期性和奇偶性;
3.会利用周期性定义和诱导公式求简单三角函数的周期;
4.借助图象直观理解正、余弦函数在[0,2π]上的性质(单调性、最值、图象与x轴的交点等);
5.能利用性质解决一些简单问题.
数学学科素养
1.数学抽象:理解周期函数、周期、最小正周期等的含义;
2.逻辑推理: 求正弦、余弦形函数的单调区间;
3.数学运算:利用性质求周期、比较大小、最值、值域及判断奇偶性.
4.数学建模:让学生借助数形结合的思想,通过图像探究正、余弦函数的性质.
学习目标
正弦函数性质的研究
定义域:
R
值 域:
[ - 1, 1 ]
x
y
o
-
-1
2
3
4
-2
-3
1
探究新知
正弦函数性质的研究
x
y
o
-
-1
2
3
4
-2
-3
1
增区间为 [ , ] 函数值从-1增至1
减区间为 [ , ] 函数值从 1减至-1
+2k , +2k ],k Z
+2k , +2k ],k Z
x
y
o
-
-1
2
3
4
-2
-3
1
单调性
探究新知
正弦函数性质的研究
x
y
o
-
-1
2
3
4
-2
-3
1
x
y
o
-
-1
2
3
4
-2
-3
1
当 时, 取得最大值1
当 时, 取得最小值-1
最 值
探究新知
x
y
o
-
-1
2
3
4
-2
-3
1
正弦函数性质的研究
对称轴:
对称中心:
对称性
探究新知
定义域:
R
值 域:
[ - 1, 1 ]
增区间:
减区间:
奇偶性:
对称轴:
对称中心:
最 值:
y
x
o
-
-1
2
3
4
-2
-3
1
小组讨论:余弦函数的性质
探究新知
余弦函数性质的研究
例1、下列函数有最大值、最小值吗? 如果有,请写出取最大值、最小值时自变量的集合,并求出最大值、最小值.
(1), ∈R; (2), ∈R.
容易知道 , 这两个函数都有最大值 、 最小值 .
(1)使函数 , ∈R取得最大值的集合 , 就是使函数 , ∈R取得最大值的 的集合{∈Z};
使函数, ∈R , 取得最小值的的集合 , 就是使函数 , ∈R取得最小值的 的集合{∈Z}.
函数, ∈R 的最大值是 1=2; 最小值是 .
解析
典例讲解
例1、下列函数有最大值、最小值吗? 如果有,请写出取最大值、最小值时自变量的集合,并求出最大值、最小值.
(1), ∈R; (2), ∈R.
解析
(2) 令 z =2, 使函数 , z∈R 取得最大值的 z 的集合 , 就是使 ,z∈R 取得最小值的 z 的集合{z=+2kπ , k ∈Z}.
由 z=2=+2kπ ,得=+kπ . 所以 , 使函数 , ∈R取得最大值的 的集合是 =+kπ, k ∈Z}.
同理 , 使函数 , ∈R取得最小值的 的集合是{=+kπ, k ∈Z}.
函数 , ∈R的最大值是, 最小值是.
典例讲解
例2、利用三角函数的单调性,比较下列各组数的大小.
且在上递增,
,即
解析
典例讲解
利用诱导公式化到同一单调区间,再根据单调性比较大小;
首先化成同名三角函数,再把角化到同一单调区间,然后比较大小.
思路
解析
(3)利用函数的单调性比较大小.
比较三角函数值大小的步骤
(1)异名函数化为同名函数;
(2)利用诱导公式把角转化到同一单调区间上;
方法归纳
变式训练
1.
.
解析
,
,
上是减函数,
上是增函数,
例3、.
当是减函数时, 是增函数,
因为函数, 的单调递减区间为 ,所以令,所以函数的单调递增区间为
解析
典例讲解
,把看作一个整体,根据函数的单调性,列出关于的不等式,求解不等式,即可得到对应的单调区间.
思路
解析
方法归纳
求函数或(其中、、 为常数, ≠0,且≠0,∈)单调性的步骤
第一步 写出函数或为增函数或减函数时满足的不等式
第二步 将视为一个整体,代入到上述不等式
第三步 解第二步中的不等式,求出的范围
第四步 下结论
当三角函数中自变量的系数为负数时,要把系数转化为正数后,再求单调区间.
变式训练
2.
.
解析
令,即,
的单调递增区间是.
变式训练
2.
.
解析
函数的单调递增区间即为函数
例4、已知是正数,函数在区间,求的取值范围.
由
得
的单调递增区间是
根据题意,得,
从而有解得 故的取值范围是 .
解析
典例讲解
根据正弦函数的单调递增区间确定函数的单调递增区间,再根据函数在区间单调递增,建立不等式组,即可求得的取值范围.
思路
解析
方法归纳
已知函数(其中,, 为常数, >0, >0)的单调区间求或,一般将代入的相应的单调区间所对应的不等式,求出的范围,对应已知的单调区间建立关于或的不等式(组)进行求解.
变式训练
3.
A. B. C. D.
解析
由 , 得,
的单调递减区间是.
根据题意,得,
从而有解得故的取值范围是
(3)形如y=Asin(ωx+φ)(A>0,ω>0)的函数的最值通常利用“整体代换”,即令ωx+φ=z,将函数转化为y=Asin z的形式求最值.
正弦函数、余弦函数最值的释疑
(1)明确正、余弦函数的有界性,即|sin x|≤1,|cos x|≤1.
(2)对有些正、余弦函数,其最值不一定是1或-1,要依赖函数定义域来决定.
素养提炼
当堂练习
1.函数的最大值及取最大值时的值为( )
2.函数的最大值是( )
3·已知函数的图象关于直线对称,则可能是( )
A.
C
C
C
当堂练习
4.下列函数中,周期为,且在区间上为减函数的是( )
A. B.
C. D.
5.函数的单调递增区间为__________________.
6.函数的单调递增区间为_________________.
B
定义域
值 域
单调性 增区间
减区间
最值
奇偶性
对称轴
对称中心
R
R
[ - 1, 1 ]
[ - 1, 1 ]
偶函数
奇函数
归纳小结
作 业
P207练习:1、2、3
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
