青岛版数学八年级上册 5.6几何证明举例(4)课件(共14张PPT)
文档属性
| 名称 | 青岛版数学八年级上册 5.6几何证明举例(4)课件(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 415.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
第4课时
5.6 几何证明举例
一、预习诊断
下列说法中,错误的是( )。
A.三角形任意两个角的平分线的交点都在三角形内部
B.三角形任意两个角的平分线的交点到三角形三边的距离相等
C.三角形任意两个角的平分线的交点都在第三个角的平分线上
D.三角形任意两个角的平分线的交点到三角形三个顶点的距离都相等
教学目标
1.掌握并证明角平分线的性质定理及其逆定理;
2.会运用角平分线的性质定理及其逆定理解决有关实际问题。
回顾与思考
1.什么叫角的平分线?
2.根据本册第二章的学习你知道角的垂直平分线有什么性质?
3.这个性质你是怎样得到的?这个性质是真命题吗?你能用逻辑推理的方法,证明它的真实性吗?
二、精讲点拨
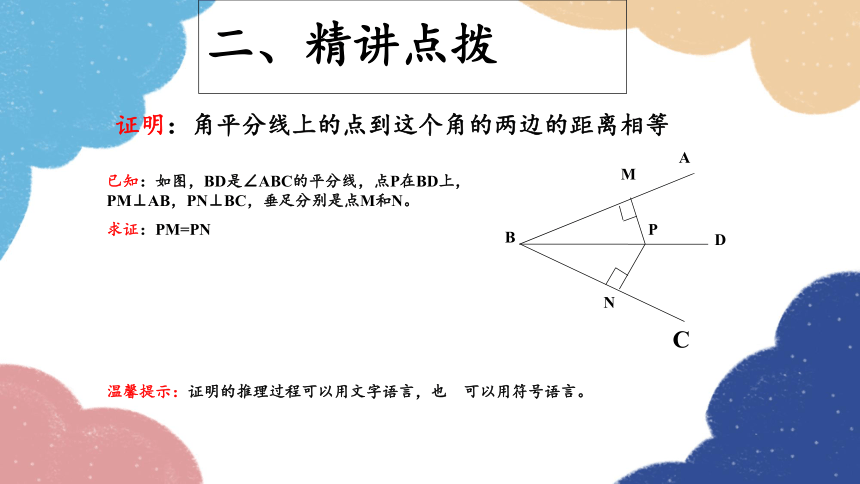
证明:角平分线上的点到这个角的两边的距离相等
P
M
N
C
B
A
D
已知:如图,BD是∠ABC的平分线,点P在BD上,PM⊥AB,PN⊥BC,垂足分别是点M和N。
求证:PM=PN
温馨提示:证明的推理过程可以用文字语言,也 可以用符号语言。
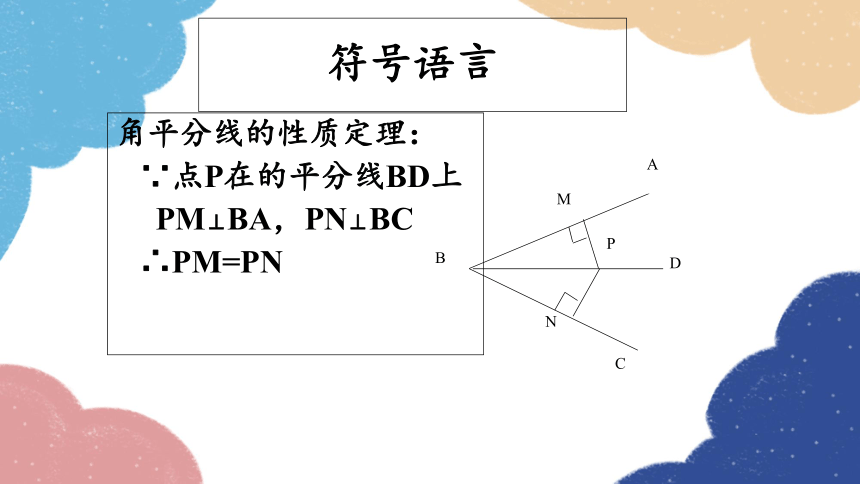
符号语言
角平分线的性质定理:
∵点P在的平分线BD上
PM⊥BA,PN⊥BC
∴PM=PN
P
M
N
C
B
A
D
交流与发现
你能说出角平分线的性质定理的逆命题吗?它是真命题吗?应如何证明它的真实性?
角的内部到角的两边距离相等的点在这个角的平分线上。
P
N
M
B
A
C
已知:如图,点P是∠ABC内的一点,PM⊥AB,PN⊥BC,垂足分别是M与N,且PM=PN。
求证:点P在∠ABC的平分线上
符号语言
角平分线的判定定理:
∵ PM⊥BA,PN⊥BC,PM=PN
∴点P在∠ABC的平分线上
(或BP是∠ABC的平分线)
P
N
M
B
A
C
典型例题
我们通过画图得知三角形三条平分线交于一点,如何证明这个结论?
例:已知:如图,AM,BN,CP是△ABC的三条角平分线。
求证:AM,BN,CP交于一点。
要证明三角形的三条角平分线交
与一点,只要证明两条角平分线
的交点也在第三条角平分线上就
可以了。
小试身手
如右图,△ABC中,AB=AC,M是BC的中点,MD⊥AB,ME⊥AC,
D、E是垂足。
求证:MD=ME。
再试身手
如下图,已知:△ABC中,∠BAC = 90°, AD⊥BC于D,AE平∠DAC,EF⊥BC交AC于F,连接BF。
求证:BF是∠ABC的平分线。
三、系统总结
1.角平分线的性质定理:
角平分线上的点到这个角两边的距离相等。
作用:证明两条线段相等
2.角平分线性质定理的逆定理:
角的内部到角的两边距离相等的点在这个角的平分线上。
作用:证明两个角相等或线是角平分线
3.符号语言:
角平分线的性质定理:
∵点P在的平分线BD上
且 PM⊥BA,PN⊥BC
∴PM=PN
角平分线的判定定理:
∵ PM⊥BA,PN⊥BC,且
PM=PN
∴点P在∠ABC的平分线上
(或BP是∠ABC的平分线)
谢 谢
第4课时
5.6 几何证明举例
一、预习诊断
下列说法中,错误的是( )。
A.三角形任意两个角的平分线的交点都在三角形内部
B.三角形任意两个角的平分线的交点到三角形三边的距离相等
C.三角形任意两个角的平分线的交点都在第三个角的平分线上
D.三角形任意两个角的平分线的交点到三角形三个顶点的距离都相等
教学目标
1.掌握并证明角平分线的性质定理及其逆定理;
2.会运用角平分线的性质定理及其逆定理解决有关实际问题。
回顾与思考
1.什么叫角的平分线?
2.根据本册第二章的学习你知道角的垂直平分线有什么性质?
3.这个性质你是怎样得到的?这个性质是真命题吗?你能用逻辑推理的方法,证明它的真实性吗?
二、精讲点拨
证明:角平分线上的点到这个角的两边的距离相等
P
M
N
C
B
A
D
已知:如图,BD是∠ABC的平分线,点P在BD上,PM⊥AB,PN⊥BC,垂足分别是点M和N。
求证:PM=PN
温馨提示:证明的推理过程可以用文字语言,也 可以用符号语言。
符号语言
角平分线的性质定理:
∵点P在的平分线BD上
PM⊥BA,PN⊥BC
∴PM=PN
P
M
N
C
B
A
D
交流与发现
你能说出角平分线的性质定理的逆命题吗?它是真命题吗?应如何证明它的真实性?
角的内部到角的两边距离相等的点在这个角的平分线上。
P
N
M
B
A
C
已知:如图,点P是∠ABC内的一点,PM⊥AB,PN⊥BC,垂足分别是M与N,且PM=PN。
求证:点P在∠ABC的平分线上
符号语言
角平分线的判定定理:
∵ PM⊥BA,PN⊥BC,PM=PN
∴点P在∠ABC的平分线上
(或BP是∠ABC的平分线)
P
N
M
B
A
C
典型例题
我们通过画图得知三角形三条平分线交于一点,如何证明这个结论?
例:已知:如图,AM,BN,CP是△ABC的三条角平分线。
求证:AM,BN,CP交于一点。
要证明三角形的三条角平分线交
与一点,只要证明两条角平分线
的交点也在第三条角平分线上就
可以了。
小试身手
如右图,△ABC中,AB=AC,M是BC的中点,MD⊥AB,ME⊥AC,
D、E是垂足。
求证:MD=ME。
再试身手
如下图,已知:△ABC中,∠BAC = 90°, AD⊥BC于D,AE平∠DAC,EF⊥BC交AC于F,连接BF。
求证:BF是∠ABC的平分线。
三、系统总结
1.角平分线的性质定理:
角平分线上的点到这个角两边的距离相等。
作用:证明两条线段相等
2.角平分线性质定理的逆定理:
角的内部到角的两边距离相等的点在这个角的平分线上。
作用:证明两个角相等或线是角平分线
3.符号语言:
角平分线的性质定理:
∵点P在的平分线BD上
且 PM⊥BA,PN⊥BC
∴PM=PN
角平分线的判定定理:
∵ PM⊥BA,PN⊥BC,且
PM=PN
∴点P在∠ABC的平分线上
(或BP是∠ABC的平分线)
谢 谢
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
