人教版数学八年级下册 17.1勾股定理课时2课件(共27张PPT)
文档属性
| 名称 | 人教版数学八年级下册 17.1勾股定理课时2课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 980.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 16:50:18 | ||
图片预览





文档简介
(共27张PPT)
17.1 勾股定理
八年级下册 RJ
初中数学
课时2
勾股定理的4种证明方法:
赵爽弦图
刘徽“青朱出入图”
加菲尔德总统拼图
毕达哥拉斯拼图
知识回顾
1.学会利用勾股定理的数学思想解决生活中的实际问题.
2.能熟练将实际问题转化为数学模型进行计算.
学习目标
这节课我们就来学习用勾股定理解决实际问题.
波平如镜一湖面,3尺高处出红莲.
亭亭多姿湖中立,突遭狂风吹一边.离开原处6尺远,花贴湖面像睡莲.请君动脑想一想,湖水在此深几尺?
课堂导入
例1 一个门框的尺寸如图所示.
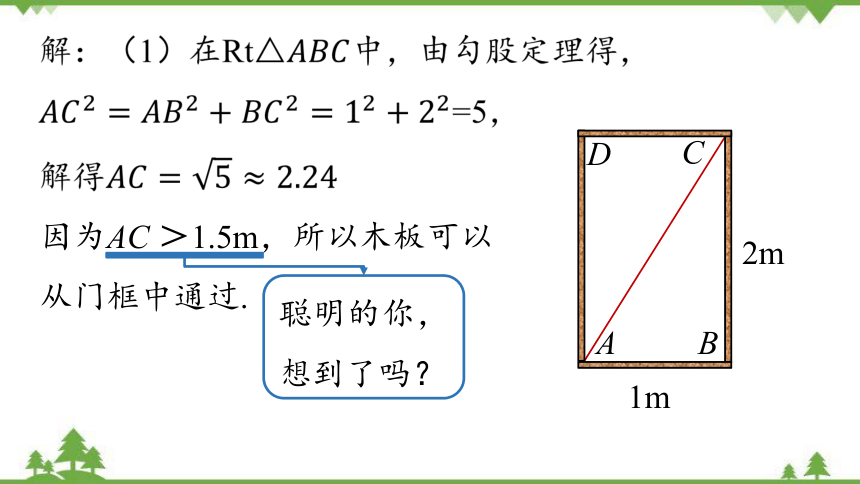
(1)一块长3m,宽1.5m的薄木板,能否从门框中通过?若能应该如何通过?
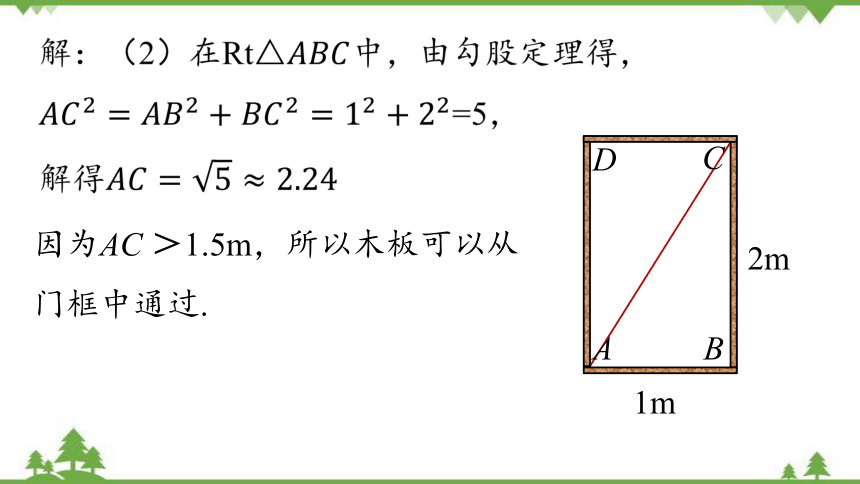
(2)一块长3m,宽2.2m的薄木板呢?
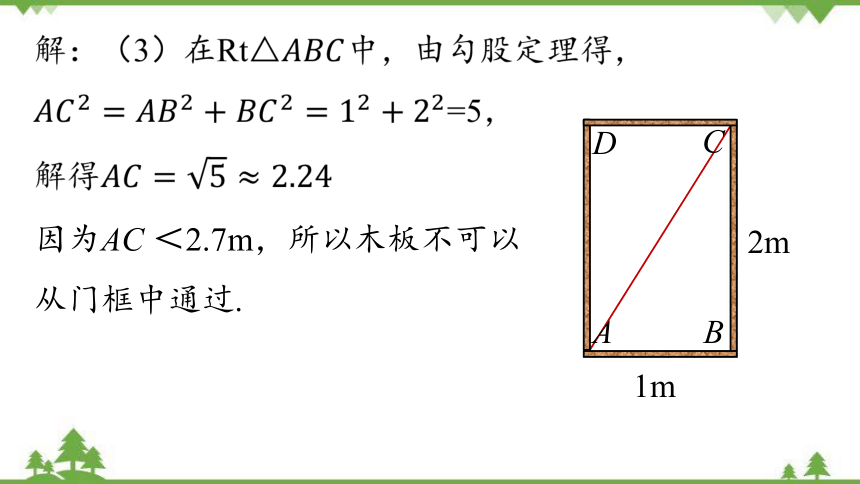
(3)一块长3m,宽2.7m的薄木板呢?heit
D
A
C
B
1m
2m
知识点:勾股定理的应用
新知探究
如何判断呢?
D
A
C
B
1m
2m
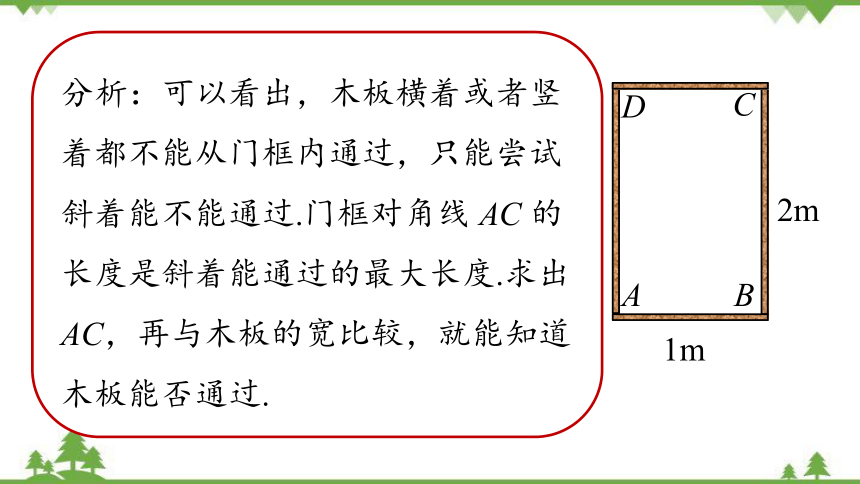
分析:可以看出,木板横着或者竖着都不能从门框内通过,只能尝试斜着能不能通过.门框对角线 AC 的长度是斜着能通过的最大长度.求出 AC,再与木板的宽比较,就能知道木板能否通过.
因为AC >1.5m,所以木板可以从门框中通过.
D
A
C
B
1m
2m
聪明的你,想到了吗?
因为AC >1.5m,所以木板可以从门框中通过.
D
A
C
B
1m
2m
因为AC <2.7m,所以木板不可以从门框中通过.
D
A
C
B
1m
2m
分析:①梯子下滑前和下滑后的长度不变;②梯子下滑前和下滑后均与墙AO和地面构成直角三角形.
例2 如图,一架 2.6m 长的梯子 AB 斜靠在一竖直的墙 AO 上,这时 AO 为 2.4m. 如果梯子的顶端 A 沿墙下滑 0.5m,那么梯子底端 B 也外移 0.5m 吗?
A
C
O
B
D
A
C
O
B
D
A
C
O
B
D
所以梯子的顶端下滑0.5m时,梯子底端并不是也外移0.5m,而是外移约0.77m.
运用勾股定理解决实际问题的一般步骤
1.从实际问题中抽象出几何图形;
2.确定所求线段所在的直角三角形;
3.找准直角边和斜边,根据勾股定理建立等量关系;
4.求得结果.
勾股定理应用的常见类型
1.已知直角三角形的任意两边求第三边;
2.已知直角三角形的任意一边确定另两边的关系;
3.证明包含有平方(算术平方根)关系的几何问题;
4.求解几何体表面上的最短路程问题;
5.构造方程(或方程组)计算有关线段长度,解决生产、生活中的实际问题.
1.在一次台风中,小红家的树在离地面 3 米的地方被拦腰截断,树的顶部落在离根部 4 米的地方,你能计算出这棵树没截断前的高度吗?
跟踪训练
新知探究
分析:根据题意,可以将地面、截断倒地的树的部分、剩余未截断的树的部分构建成一个直角三角形.
不要忘记这一步哦!
A
C
B
A
C
B
分析:根据勾股定理可以得出直角三角形的第三边也相等,然后利用“三边相等”来证明全等.
1.如图,池塘边有两点 A,B,点 C 是与 BA 方向成直角的AC 方向上一点,测得 BC=60m,AC=20m. 求 A,B 两点间的距离(结果取整数).
A
B
C
随堂练习
2.(2021 宿迁中考)《九章算术》中一道“引葭赴岸”问题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?”题意是:有一个池塘,其地面是边长为10尺的正方形,一棵芦苇AC生长在它的中央,高出水面部分BC为1尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部C恰好碰到岸边的C'处(如图1),水深和芦苇长各多少尺?则该问题的水深是 ______尺.
解:把台阶展成如图的平面图形,连接AB.
3.如图,台阶下 A 处的蚂蚁要爬到 B 处搬运食物,它走的最短路程是多少?
勾股定理的应用
实际问题
数学问题
勾股定理
直角三角形
转化
构建
运用
解决
课堂小结
1.小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为 0.7 米,顶端距离地面 2.4 米.如果保持梯子底端位置不动,
将梯子斜靠在右墙时,顶端距
离地面 2米,则小巷的宽度为
( ).
C
A. 0.7米 B. 1.5米
C. 2.2米 D. 2.4米
0.7
2.4
2.5
2
1.5
拓展提升
2.已知一个三角形工件尺寸如图,计算高 l 的长(结果取整数).
解:如图,过点A作AD⊥BC于点D.
A
B
C
D
l
88mm
64mm
88mm
3.有一块土地形状如图所示, ∠B=∠D=90 ,AB=20米,BC=15米, CD=7米,请计算这块土地的面积.
解:连接AC,则S四边形ABCD= S△ABC + S△ADC.
答:这块土地的面积为234平方米.
17.1 勾股定理
八年级下册 RJ
初中数学
课时2
勾股定理的4种证明方法:
赵爽弦图
刘徽“青朱出入图”
加菲尔德总统拼图
毕达哥拉斯拼图
知识回顾
1.学会利用勾股定理的数学思想解决生活中的实际问题.
2.能熟练将实际问题转化为数学模型进行计算.
学习目标
这节课我们就来学习用勾股定理解决实际问题.
波平如镜一湖面,3尺高处出红莲.
亭亭多姿湖中立,突遭狂风吹一边.离开原处6尺远,花贴湖面像睡莲.请君动脑想一想,湖水在此深几尺?
课堂导入
例1 一个门框的尺寸如图所示.
(1)一块长3m,宽1.5m的薄木板,能否从门框中通过?若能应该如何通过?
(2)一块长3m,宽2.2m的薄木板呢?
(3)一块长3m,宽2.7m的薄木板呢?heit
D
A
C
B
1m
2m
知识点:勾股定理的应用
新知探究
如何判断呢?
D
A
C
B
1m
2m
分析:可以看出,木板横着或者竖着都不能从门框内通过,只能尝试斜着能不能通过.门框对角线 AC 的长度是斜着能通过的最大长度.求出 AC,再与木板的宽比较,就能知道木板能否通过.
因为AC >1.5m,所以木板可以从门框中通过.
D
A
C
B
1m
2m
聪明的你,想到了吗?
因为AC >1.5m,所以木板可以从门框中通过.
D
A
C
B
1m
2m
因为AC <2.7m,所以木板不可以从门框中通过.
D
A
C
B
1m
2m
分析:①梯子下滑前和下滑后的长度不变;②梯子下滑前和下滑后均与墙AO和地面构成直角三角形.
例2 如图,一架 2.6m 长的梯子 AB 斜靠在一竖直的墙 AO 上,这时 AO 为 2.4m. 如果梯子的顶端 A 沿墙下滑 0.5m,那么梯子底端 B 也外移 0.5m 吗?
A
C
O
B
D
A
C
O
B
D
A
C
O
B
D
所以梯子的顶端下滑0.5m时,梯子底端并不是也外移0.5m,而是外移约0.77m.
运用勾股定理解决实际问题的一般步骤
1.从实际问题中抽象出几何图形;
2.确定所求线段所在的直角三角形;
3.找准直角边和斜边,根据勾股定理建立等量关系;
4.求得结果.
勾股定理应用的常见类型
1.已知直角三角形的任意两边求第三边;
2.已知直角三角形的任意一边确定另两边的关系;
3.证明包含有平方(算术平方根)关系的几何问题;
4.求解几何体表面上的最短路程问题;
5.构造方程(或方程组)计算有关线段长度,解决生产、生活中的实际问题.
1.在一次台风中,小红家的树在离地面 3 米的地方被拦腰截断,树的顶部落在离根部 4 米的地方,你能计算出这棵树没截断前的高度吗?
跟踪训练
新知探究
分析:根据题意,可以将地面、截断倒地的树的部分、剩余未截断的树的部分构建成一个直角三角形.
不要忘记这一步哦!
A
C
B
A
C
B
分析:根据勾股定理可以得出直角三角形的第三边也相等,然后利用“三边相等”来证明全等.
1.如图,池塘边有两点 A,B,点 C 是与 BA 方向成直角的AC 方向上一点,测得 BC=60m,AC=20m. 求 A,B 两点间的距离(结果取整数).
A
B
C
随堂练习
2.(2021 宿迁中考)《九章算术》中一道“引葭赴岸”问题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?”题意是:有一个池塘,其地面是边长为10尺的正方形,一棵芦苇AC生长在它的中央,高出水面部分BC为1尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部C恰好碰到岸边的C'处(如图1),水深和芦苇长各多少尺?则该问题的水深是 ______尺.
解:把台阶展成如图的平面图形,连接AB.
3.如图,台阶下 A 处的蚂蚁要爬到 B 处搬运食物,它走的最短路程是多少?
勾股定理的应用
实际问题
数学问题
勾股定理
直角三角形
转化
构建
运用
解决
课堂小结
1.小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为 0.7 米,顶端距离地面 2.4 米.如果保持梯子底端位置不动,
将梯子斜靠在右墙时,顶端距
离地面 2米,则小巷的宽度为
( ).
C
A. 0.7米 B. 1.5米
C. 2.2米 D. 2.4米
0.7
2.4
2.5
2
1.5
拓展提升
2.已知一个三角形工件尺寸如图,计算高 l 的长(结果取整数).
解:如图,过点A作AD⊥BC于点D.
A
B
C
D
l
88mm
64mm
88mm
3.有一块土地形状如图所示, ∠B=∠D=90 ,AB=20米,BC=15米, CD=7米,请计算这块土地的面积.
解:连接AC,则S四边形ABCD= S△ABC + S△ADC.
答:这块土地的面积为234平方米.
