相似三角形的判定定理[上学期]
文档属性
| 名称 | 相似三角形的判定定理[上学期] | 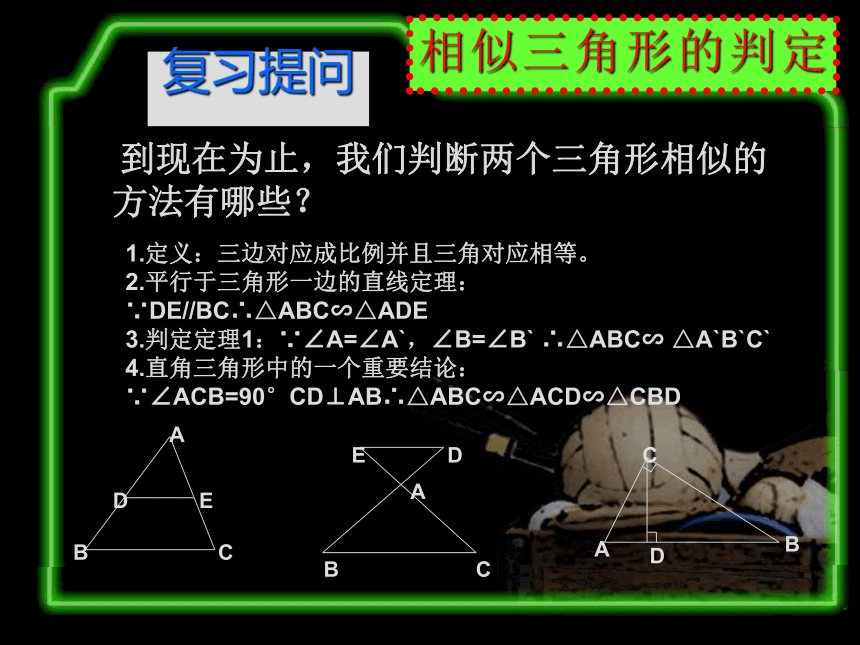 | |
| 格式 | rar | ||
| 文件大小 | 77.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-30 09:29:00 | ||
图片预览


文档简介
课件13张PPT。复习提问 到现在为止,我们判断两个三角形相似的方法有哪些?1.定义:三边对应成比例并且三角对应相等。
2.平行于三角形一边的直线定理:∵DE//BC∴△ABC∽△ADE
3.判定定理1:∵∠A=∠A`,∠B=∠B` ∴△ABC∽ △A`B`C`
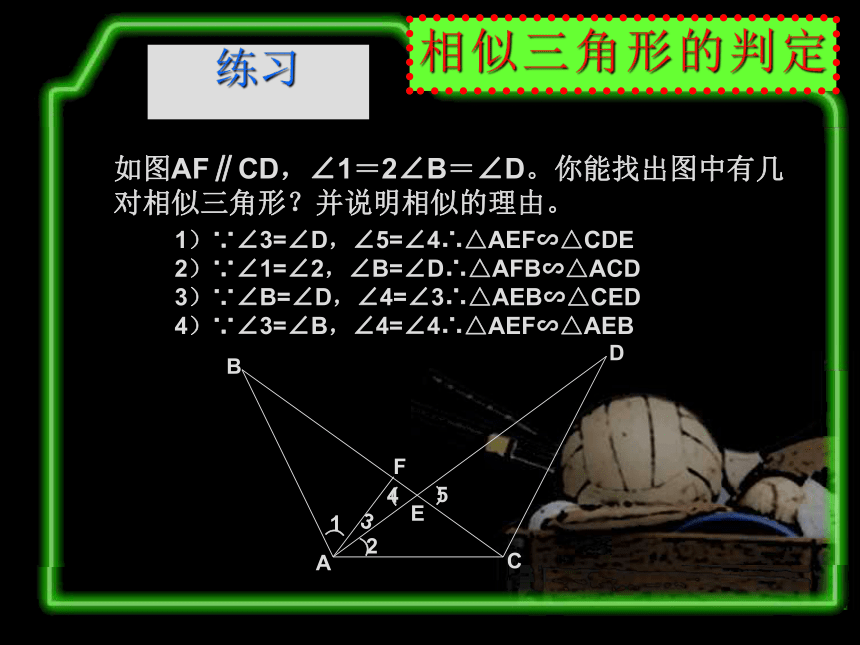
4.直角三角形中的一个重要结论:∵∠ACB=90°CD⊥AB∴△ABC∽△ACD∽△CBD练习如图AF∥CD,∠1=2∠B=∠D。你能找出图中有几对相似三角形?并说明相似的理由。1)∵∠3=∠D,∠5=∠4∴△AEF∽△CDE
2)∵∠1=∠2,∠B=∠D∴△AFB∽△ACD
3)∵∠B=∠D,∠4=∠3∴△AEB∽△CED
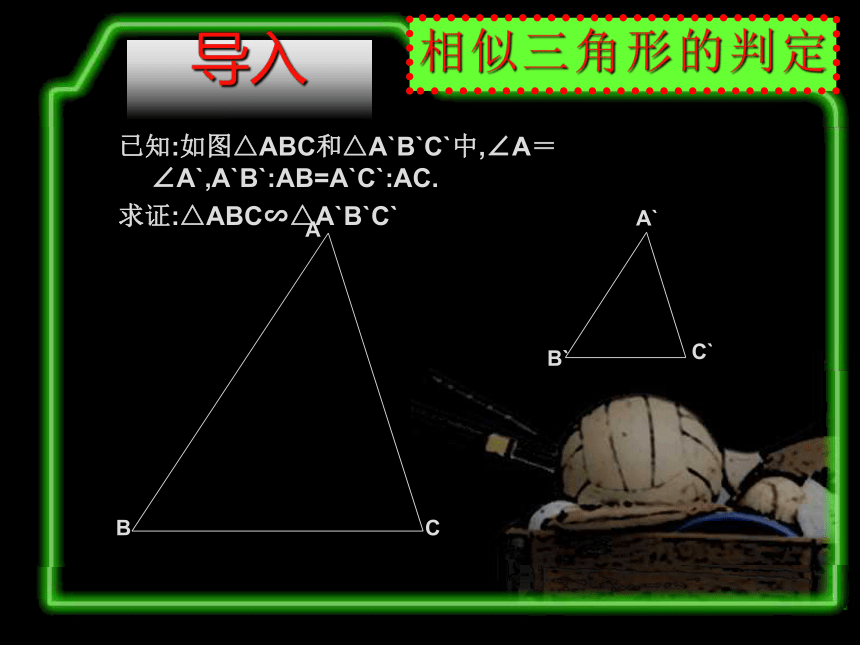
4)∵∠3=∠B,∠4=∠4∴△AEF∽△AEB导入已知:如图△ABC和△A`B`C`中,∠A=∠A`,A`B`:AB=A`C`:AC.
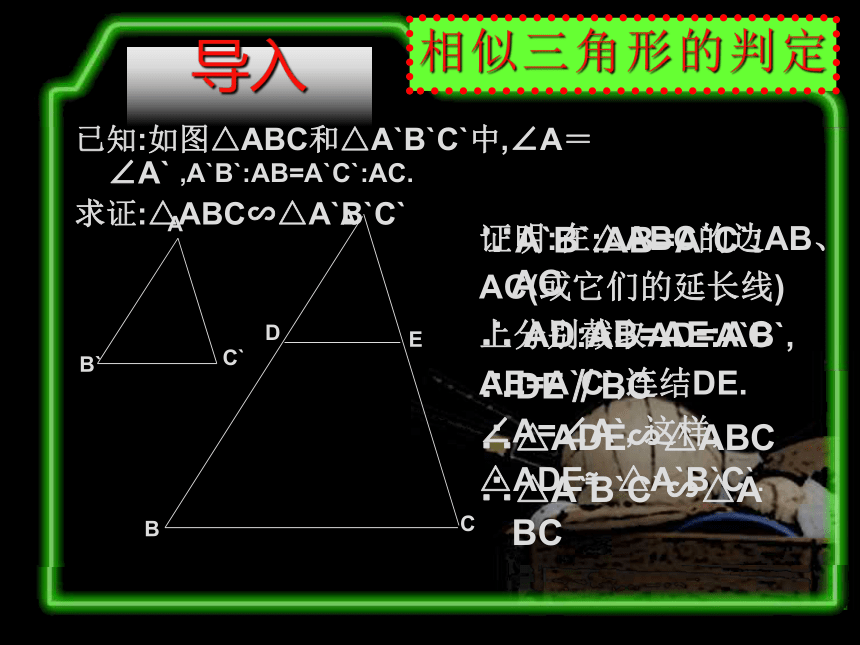
求证:△ABC∽△A`B`C`导入已知:如图△ABC和△A`B`C`中,∠A=∠A` ,A`B`:AB=A`C`:AC.
求证:△ABC∽△A`B`C`证明:在△ABC的边AB、
AC(或它们的延长线)
上分别截取AD=A`B`,
AE=A`C`,连结DE.
∠A=∠A`, 这样,
△ADE≌△A`B`C`.∵A`B`:AB=A`C`:AC
∴ AD:AB=AE:AC
∴DE∥BC
∴△ADE∽△ABC
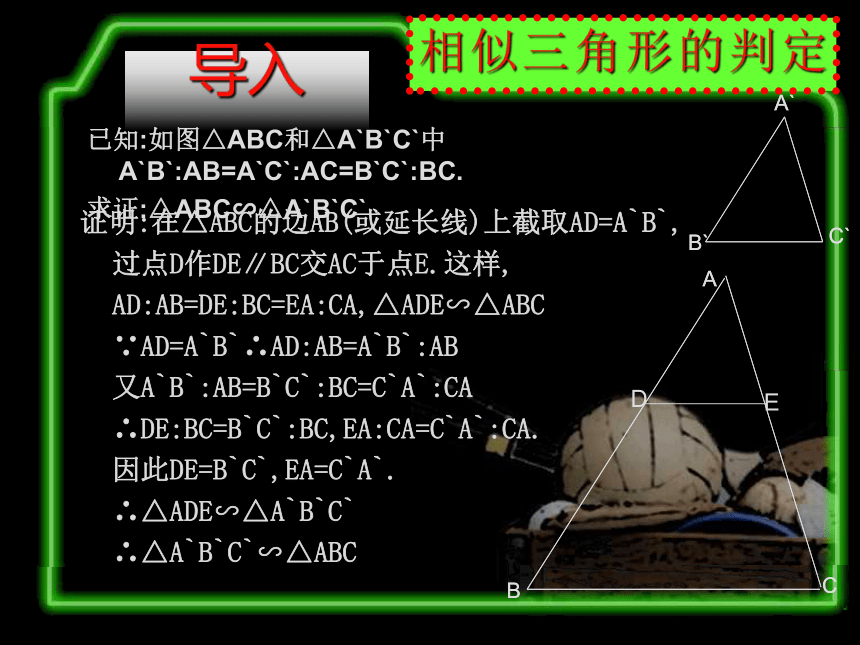
∴△A`B`C`∽△ABC判定定理2 如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似. 简单地说成:两边对应成比例且夹角相等,两三角形相似.导入已知:如图△ABC和△A`B`C`中A`B`:AB=A`C`:AC=B`C`:BC.
求证:△ABC∽△A`B`C`证明:在△ABC的边AB(或延长线)上截取AD=A`B`,
过点D作DE∥BC交AC于点E.这样,
AD:AB=DE:BC=EA:CA,△ADE∽△ABC
∵AD=A`B`∴AD:AB=A`B`:AB
又A`B`:AB=B`C`:BC=C`A`:CA
∴DE:BC=B`C`:BC,EA:CA=C`A`:CA.
因此DE=B`C`,EA=C`A`.
∴△ADE∽△A`B`C`
∴△A`B`C`∽△ABC判定定理3 如果一个三角形的三条边和另一个三角形的三条边对应成比例,那么这两个三角形相似.简单地说:三边对应成比例,两三角形相似.例题 依据下列各组条件,判定△ABC与△A`B`C`是不是相似,并说明为什么:
(1)∠A=120°,AB=7cm,AC=14cm,
∠A`=120°,A`B`=3cm,A`C`=6cm;
(2)AB=4cm,BC=6cm,AC=8cm,
A`B`=12cm,B`C`=18cm,A`C`=24cm.解:(1)∵AB:A`B`=7:3,AC:A`C`=14:6=7:3 ∴AB:A`B`=AC:A`C`
又∠A=∠A`∴△ABC∽△A`B`C`(判定定理2)(2)∵AB:A`B`=4:12=1:3,BC:B`C`=6:18=1:3,AC:A`C`=8:24=1:3,
∴ AB:A`B`= BC:B`C`= AC:A`C`
∴ △ABC∽△A`B`C`(判定定理3)练习 1.依据下列各组条件,判定△ABC与△A`B`C`是不是相似,并说明为什么:
(1)∠A=45°,AB=12厘米,AC=15厘米,
∠A`=45°,A`B`=16厘米,A`C`=20厘米;
(2)AB=12厘米,BC=15厘米,AC=24厘米,
A`B`=20厘米,B`C`=25厘米,A`C`=40厘米.解:(1)∵AB:A`B`=12:15=4:5,
AC:A`C`=16:20=4:5
∴AB:A`B`=AC:A`C`
又∠A=∠A`
∴△ABC∽△A`B`C`(判定2)(2)∵AB:A`B`=12:20=3:5, BC:B`C`=15:25=3:5,
AC:A`C`=24:40=3:5,
∴ AB:A`B`= BC:B`C`= AC:A`C`
∴ △ABC∽△A`B`C`(判定3)练习2.△ABC ,∠A=47°,AB=1.5cm,AC=2cm,
△DEF, ∠E=47°,ED=2.8cm,EF=2.1cm.
这两个三角形相似吗?为什么?如果相似,写出表示式.答:相似.∵∠A=∠E=47°AB:EF=1.5:2.1=5:7 AC:ED=2:2.8=5:7
∴△ABC∽△DEF(判定定理2)练习3.要作两个形状相同的三角形框架,其中一个三角形的三边的长分别为4、5、6,另一个三角形框架的一边长为2,怎样选料可使这两个三角形相似?这个问题有其他答案吗?4:2=5:x=6:y
4:x=5:2=6:y
4:x=5:y=6:2小结1.定义:三边对应成比例并且三角对应相等。
2.平行于三角形一边的直线定理:∵DE//BC∴△ABC∽△ADE
3.判定定理1:∵∠A=∠A`,∠B=∠B` ∴△ABC∽ △A`B`C`
4.直角三角形中的一个重要结论:∵∠ACB=90°CD⊥AB∴△ABC∽△ACD∽△CBD
5.判定定理2:∵AB:A`B`=BC:B`C`, ∠B=∠B` ∴△ABC∽ △A`B`C`
6.判定定理3: :∵AB:A`B`=BC:B`C`=AC:A`C` ∴△ABC∽ △A`B`C`作业正式作业:
课本P239. A组.第9,10题
练习作业:
B组.第1,2题制作人:李建辉
时间:2004年5月20日
2.平行于三角形一边的直线定理:∵DE//BC∴△ABC∽△ADE
3.判定定理1:∵∠A=∠A`,∠B=∠B` ∴△ABC∽ △A`B`C`
4.直角三角形中的一个重要结论:∵∠ACB=90°CD⊥AB∴△ABC∽△ACD∽△CBD练习如图AF∥CD,∠1=2∠B=∠D。你能找出图中有几对相似三角形?并说明相似的理由。1)∵∠3=∠D,∠5=∠4∴△AEF∽△CDE
2)∵∠1=∠2,∠B=∠D∴△AFB∽△ACD
3)∵∠B=∠D,∠4=∠3∴△AEB∽△CED
4)∵∠3=∠B,∠4=∠4∴△AEF∽△AEB导入已知:如图△ABC和△A`B`C`中,∠A=∠A`,A`B`:AB=A`C`:AC.
求证:△ABC∽△A`B`C`导入已知:如图△ABC和△A`B`C`中,∠A=∠A` ,A`B`:AB=A`C`:AC.
求证:△ABC∽△A`B`C`证明:在△ABC的边AB、
AC(或它们的延长线)
上分别截取AD=A`B`,
AE=A`C`,连结DE.
∠A=∠A`, 这样,
△ADE≌△A`B`C`.∵A`B`:AB=A`C`:AC
∴ AD:AB=AE:AC
∴DE∥BC
∴△ADE∽△ABC
∴△A`B`C`∽△ABC判定定理2 如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似. 简单地说成:两边对应成比例且夹角相等,两三角形相似.导入已知:如图△ABC和△A`B`C`中A`B`:AB=A`C`:AC=B`C`:BC.
求证:△ABC∽△A`B`C`证明:在△ABC的边AB(或延长线)上截取AD=A`B`,
过点D作DE∥BC交AC于点E.这样,
AD:AB=DE:BC=EA:CA,△ADE∽△ABC
∵AD=A`B`∴AD:AB=A`B`:AB
又A`B`:AB=B`C`:BC=C`A`:CA
∴DE:BC=B`C`:BC,EA:CA=C`A`:CA.
因此DE=B`C`,EA=C`A`.
∴△ADE∽△A`B`C`
∴△A`B`C`∽△ABC判定定理3 如果一个三角形的三条边和另一个三角形的三条边对应成比例,那么这两个三角形相似.简单地说:三边对应成比例,两三角形相似.例题 依据下列各组条件,判定△ABC与△A`B`C`是不是相似,并说明为什么:
(1)∠A=120°,AB=7cm,AC=14cm,
∠A`=120°,A`B`=3cm,A`C`=6cm;
(2)AB=4cm,BC=6cm,AC=8cm,
A`B`=12cm,B`C`=18cm,A`C`=24cm.解:(1)∵AB:A`B`=7:3,AC:A`C`=14:6=7:3 ∴AB:A`B`=AC:A`C`
又∠A=∠A`∴△ABC∽△A`B`C`(判定定理2)(2)∵AB:A`B`=4:12=1:3,BC:B`C`=6:18=1:3,AC:A`C`=8:24=1:3,
∴ AB:A`B`= BC:B`C`= AC:A`C`
∴ △ABC∽△A`B`C`(判定定理3)练习 1.依据下列各组条件,判定△ABC与△A`B`C`是不是相似,并说明为什么:
(1)∠A=45°,AB=12厘米,AC=15厘米,
∠A`=45°,A`B`=16厘米,A`C`=20厘米;
(2)AB=12厘米,BC=15厘米,AC=24厘米,
A`B`=20厘米,B`C`=25厘米,A`C`=40厘米.解:(1)∵AB:A`B`=12:15=4:5,
AC:A`C`=16:20=4:5
∴AB:A`B`=AC:A`C`
又∠A=∠A`
∴△ABC∽△A`B`C`(判定2)(2)∵AB:A`B`=12:20=3:5, BC:B`C`=15:25=3:5,
AC:A`C`=24:40=3:5,
∴ AB:A`B`= BC:B`C`= AC:A`C`
∴ △ABC∽△A`B`C`(判定3)练习2.△ABC ,∠A=47°,AB=1.5cm,AC=2cm,
△DEF, ∠E=47°,ED=2.8cm,EF=2.1cm.
这两个三角形相似吗?为什么?如果相似,写出表示式.答:相似.∵∠A=∠E=47°AB:EF=1.5:2.1=5:7 AC:ED=2:2.8=5:7
∴△ABC∽△DEF(判定定理2)练习3.要作两个形状相同的三角形框架,其中一个三角形的三边的长分别为4、5、6,另一个三角形框架的一边长为2,怎样选料可使这两个三角形相似?这个问题有其他答案吗?4:2=5:x=6:y
4:x=5:2=6:y
4:x=5:y=6:2小结1.定义:三边对应成比例并且三角对应相等。
2.平行于三角形一边的直线定理:∵DE//BC∴△ABC∽△ADE
3.判定定理1:∵∠A=∠A`,∠B=∠B` ∴△ABC∽ △A`B`C`
4.直角三角形中的一个重要结论:∵∠ACB=90°CD⊥AB∴△ABC∽△ACD∽△CBD
5.判定定理2:∵AB:A`B`=BC:B`C`, ∠B=∠B` ∴△ABC∽ △A`B`C`
6.判定定理3: :∵AB:A`B`=BC:B`C`=AC:A`C` ∴△ABC∽ △A`B`C`作业正式作业:
课本P239. A组.第9,10题
练习作业:
B组.第1,2题制作人:李建辉
时间:2004年5月20日
