1.1.分数乘整数(课件)-六年级上册数学青岛版(共20张PPT)
文档属性
| 名称 | 1.1.分数乘整数(课件)-六年级上册数学青岛版(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 874.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 09:30:30 | ||
图片预览







文档简介
(共20张PPT)
1.1.分数乘整数
分数乘整数的算式是怎么样的?举几个例子。
7
4
×5
2
1
×5
2
1
×6
8
3
2×
……
想一想
上面各个算式表示什么意思?
分数乘整数怎么计算?
把自己的想法写下来,并思考还有其他计算方法吗?
自主探索
2
1
×5
以 为例,初步感知分数乘整数的计算方法。
展示算法,并分析比较。
初步感知
算法展示
2
1
×5
= 0.5×5=2.5
2
1
×5
=
2
1×5
=
2
5
01
02
03
04
10
5
=
2
1
×5
=
2×5
1×5
2
1
×5
2
1
+
2
1
+
2
1
+
2
1
+
2
1
=
=
2
5
算法交流
2
1
×5
= 0.5×5=2.5
2
1
×5
=
2
1×5
=
2
5
01
02
03
04
10
5
=
2
1
×5
=
2×5
1×5
2
1
×5
2
1
+
2
1
+
2
1
+
2
1
+
2
1
=
=
2
5
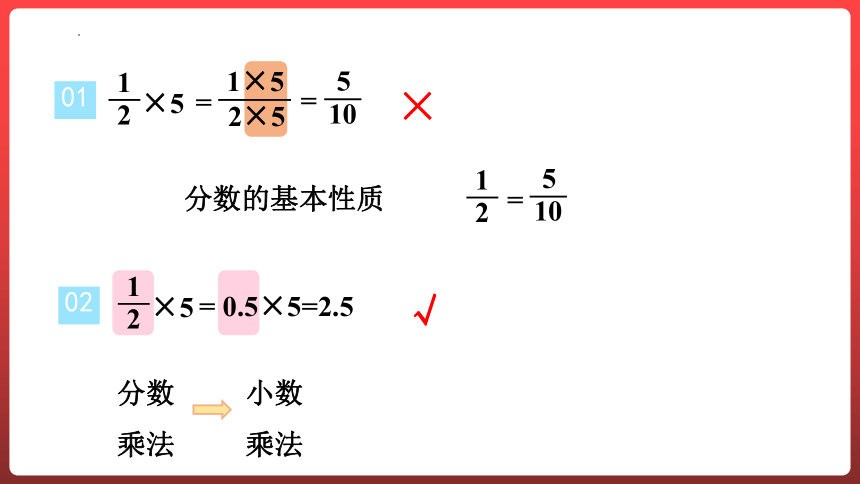
这四种方法正确吗?
为什么?依次分析。
02
×
01
分数的基本性质
10
5
=
2
1
分数乘法
√
小数乘法
10
5
=
2
1
×5
=
2×5
1×5
2
1
×5
= 0.5×5=2.5
2
1
×5
=
2
1
+
2
1
+
2
1
+
2
1
+
2
1
=
2
1+1+1+1+1
=
2
5
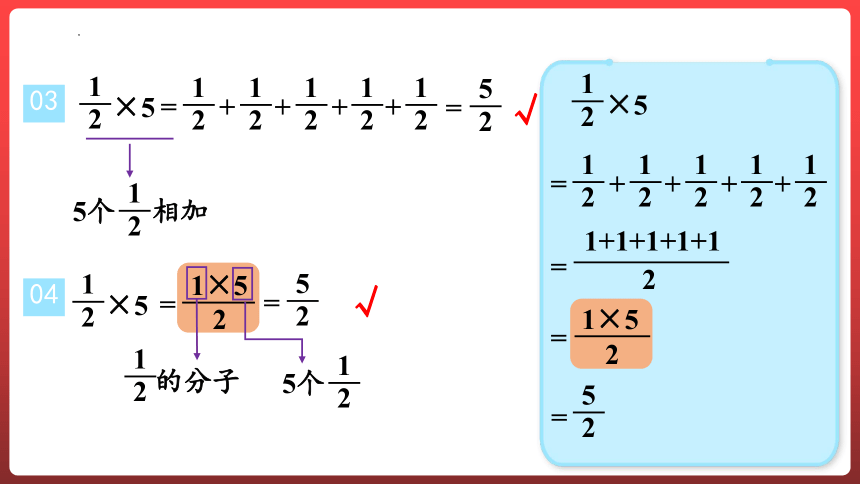
03
04
5个 相加
2
1
√
√
2
1
×5
=
2
5
2
1
×5
=
2
1×5
=
2
5
=
2
1
+
2
1
+
2
1
+
2
1
+
2
1
的分子
2
1
5个
2
1
=
2
1×5
分数乘整数的意义与整数乘法的意义相同,
都是求几个相同加数和的简便运算。
你能用刚才的方法找到 的结果吗?
4
7
×3
再在班内展示算法,交流自己的想法,交流时要把道理说清楚。相互质疑、补充、比较。
自主探索
先用自己喜欢的方法计算 。
7
4
×3
强化感知
算法展示
7
4
×3
=
7
4×3
01
02
7
4
×3
7
4
+
7
4
+
7
4
=
7
12
=
7
12
=
为什么没用分数化小数的方法?
思考
7
4
=4÷7≈0.571
除不尽,有局限性
算法交流
7
4
×3
=
7
4×3
01
02
7
4
× 3
7
4
+
7
4
+
7
4
=
7
12
=
7
12
=
哪种方法更简便?
100
数量越多,越繁琐
7
4
+
7
4
+ ……
7
4
+
算法交流
7
4
×3
=
7
4×3
7
12
=
4表示什么?
3表示什么?
为什么可以写成4×3?
7
4
×3
=
7
4
+
7
4
+
7
4
=
7
4+4+4
=
7
4×3
=
7
12
省略不写
用分数的分子和整数
相乘的积作分子,
分母不变。
算法交流
7
4
×3
=
7
4×3
=
7
12
2
9
×4
1
2
×6
2×4
9
=
8
9
=
1×6
2
=
3
6
2
=
你会算吗?
1
3
=
化成最简分数!
想一想,算一算。
3
8
×12
13
49
7×
3×12
8
=
36
8
=
9
2
9
2
=
7×13
49
=
7
1
13
7
=
先独立计算,再交流
展示。
看看自己的方法与别
人的有什么不同之处?
3
8
×12
13
49
7×
3×12
8
=
36
8
=
9
2
=
7×13
49
=
7
1
13
7
=
或
13
49
= 7×
1
7
13
7
=
13
49
7×
观察两道题目的计算方法,有什么不同?
先计算,再约分
先约分,再计算
计算简便
9
2
算法总结
7
4
×3
=
7
4×3
7
12
=
2
1
×5
=
2
1×5
=
2
5
13
49
7×
7×13
49
=
7
1
13
7
=
分数乘整数,分子乘整数的积作分子,分母不变。
能约分的,先约分,再计算,更简便。
1.下面的算法对吗?若不对,请改正。
×
9
10
9
10
×6=
×6=
10
6
=
3
2
3
5
=
9
10
9
10
×6=
×6
27
5
=
5
3
分子与整数不能约分
2.下面的算法简便吗?若不简便,请用简便方法算。
5
16
×12
5×12
16
=
60
16
=
4
15
15
4
=
不简便
5
16
×12
×12
5
16
=
4
3
15
4
=
5
16
×12
5×12
16
=
4
3
15
4
=
或
出示课题,引导提问
学生尝试,初步感知
强化感知,建立算法
灵活运用,提升能力
1.1.分数乘整数
分数乘整数的算式是怎么样的?举几个例子。
7
4
×5
2
1
×5
2
1
×6
8
3
2×
……
想一想
上面各个算式表示什么意思?
分数乘整数怎么计算?
把自己的想法写下来,并思考还有其他计算方法吗?
自主探索
2
1
×5
以 为例,初步感知分数乘整数的计算方法。
展示算法,并分析比较。
初步感知
算法展示
2
1
×5
= 0.5×5=2.5
2
1
×5
=
2
1×5
=
2
5
01
02
03
04
10
5
=
2
1
×5
=
2×5
1×5
2
1
×5
2
1
+
2
1
+
2
1
+
2
1
+
2
1
=
=
2
5
算法交流
2
1
×5
= 0.5×5=2.5
2
1
×5
=
2
1×5
=
2
5
01
02
03
04
10
5
=
2
1
×5
=
2×5
1×5
2
1
×5
2
1
+
2
1
+
2
1
+
2
1
+
2
1
=
=
2
5
这四种方法正确吗?
为什么?依次分析。
02
×
01
分数的基本性质
10
5
=
2
1
分数乘法
√
小数乘法
10
5
=
2
1
×5
=
2×5
1×5
2
1
×5
= 0.5×5=2.5
2
1
×5
=
2
1
+
2
1
+
2
1
+
2
1
+
2
1
=
2
1+1+1+1+1
=
2
5
03
04
5个 相加
2
1
√
√
2
1
×5
=
2
5
2
1
×5
=
2
1×5
=
2
5
=
2
1
+
2
1
+
2
1
+
2
1
+
2
1
的分子
2
1
5个
2
1
=
2
1×5
分数乘整数的意义与整数乘法的意义相同,
都是求几个相同加数和的简便运算。
你能用刚才的方法找到 的结果吗?
4
7
×3
再在班内展示算法,交流自己的想法,交流时要把道理说清楚。相互质疑、补充、比较。
自主探索
先用自己喜欢的方法计算 。
7
4
×3
强化感知
算法展示
7
4
×3
=
7
4×3
01
02
7
4
×3
7
4
+
7
4
+
7
4
=
7
12
=
7
12
=
为什么没用分数化小数的方法?
思考
7
4
=4÷7≈0.571
除不尽,有局限性
算法交流
7
4
×3
=
7
4×3
01
02
7
4
× 3
7
4
+
7
4
+
7
4
=
7
12
=
7
12
=
哪种方法更简便?
100
数量越多,越繁琐
7
4
+
7
4
+ ……
7
4
+
算法交流
7
4
×3
=
7
4×3
7
12
=
4表示什么?
3表示什么?
为什么可以写成4×3?
7
4
×3
=
7
4
+
7
4
+
7
4
=
7
4+4+4
=
7
4×3
=
7
12
省略不写
用分数的分子和整数
相乘的积作分子,
分母不变。
算法交流
7
4
×3
=
7
4×3
=
7
12
2
9
×4
1
2
×6
2×4
9
=
8
9
=
1×6
2
=
3
6
2
=
你会算吗?
1
3
=
化成最简分数!
想一想,算一算。
3
8
×12
13
49
7×
3×12
8
=
36
8
=
9
2
9
2
=
7×13
49
=
7
1
13
7
=
先独立计算,再交流
展示。
看看自己的方法与别
人的有什么不同之处?
3
8
×12
13
49
7×
3×12
8
=
36
8
=
9
2
=
7×13
49
=
7
1
13
7
=
或
13
49
= 7×
1
7
13
7
=
13
49
7×
观察两道题目的计算方法,有什么不同?
先计算,再约分
先约分,再计算
计算简便
9
2
算法总结
7
4
×3
=
7
4×3
7
12
=
2
1
×5
=
2
1×5
=
2
5
13
49
7×
7×13
49
=
7
1
13
7
=
分数乘整数,分子乘整数的积作分子,分母不变。
能约分的,先约分,再计算,更简便。
1.下面的算法对吗?若不对,请改正。
×
9
10
9
10
×6=
×6=
10
6
=
3
2
3
5
=
9
10
9
10
×6=
×6
27
5
=
5
3
分子与整数不能约分
2.下面的算法简便吗?若不简便,请用简便方法算。
5
16
×12
5×12
16
=
60
16
=
4
15
15
4
=
不简便
5
16
×12
×12
5
16
=
4
3
15
4
=
5
16
×12
5×12
16
=
4
3
15
4
=
或
出示课题,引导提问
学生尝试,初步感知
强化感知,建立算法
灵活运用,提升能力
