3.1.分数除以整数(课件)-六年级上册数学青岛版(共22张PPT)
文档属性
| 名称 | 3.1.分数除以整数(课件)-六年级上册数学青岛版(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 09:34:26 | ||
图片预览







文档简介
(共22张PPT)
3.1.分数除以整数
5
1
×
2
1
=
5
3
×
4
3
=
7
4
×
5
3
=
8
5
×
5
3
=
10
1
35
12
20
9
8
3
回顾一下,我们是怎样学习分数乘法的?
布艺兴趣小组用 米布料给小猴做背心,可以做3件;用 米布料做裤子,可以做2条。
9
10
5
6
阅读题目,想一想你能提出哪些数学问题?
做一件背心需要布料多少米?
做一条裤子需要布料多少米?
用 米布料可以做3件背心,做一件背心需要布料多少米?
10
9
怎样列式?为什么这样列式?
10
9
÷ 3
平均分
仔细观察这个算式,找一找与我们以前学习过的除法算式有哪些地方相同,哪些地方不同?
同桌合作
分数除以整数
想一想:能利用以前学过的知识计算 吗?
做一做:把你的想法写在练习本上。
说一说:在小组内交流你的计算方法。
评一评:小组成员对每种算法进行评价、质疑。
自主探究
10
9
÷3
算法展示
9
10
÷3
=0.9÷3=0.3(米)
方法一:
9
10
÷3
=
方法二:
9÷3
10
=
3
10
(米)
9
10
÷3
=
方法三:
=
3
10
(米)
9
10
×
1
3
3
1
仔细观察,你的方法与哪种方法相同?你能看懂这些方法吗?
算法
分
析
9
10
÷3
=0.9÷3=0.3(米)
方法一:
你是怎样想的?为什么要把它化成小数?
运用了哪种常用的数学方法?
把分数转化成小数计算
分数除以整数
小数除法
转化
算法
分
析
为什么这样算?这样算的依据是什么?
谁能借助直观图来讲一讲?
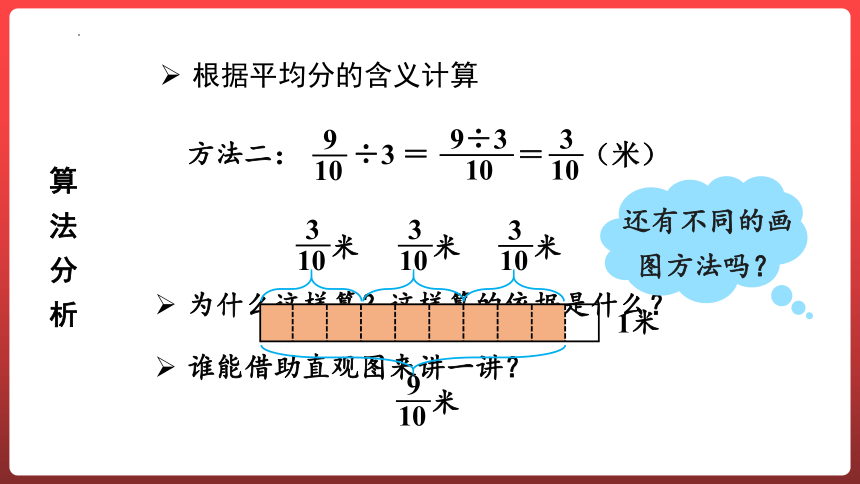
根据平均分的含义计算
9
10
÷3
=
方法二:
9÷3
10
=
3
10
(米)
1米
3
10
9
10
3
10
3
10
还有不同的画图方法吗?
米
米
米
米
算法
分
析
对于这种方法,你们有疑问吗?
谁能借助直观图来讲一讲?
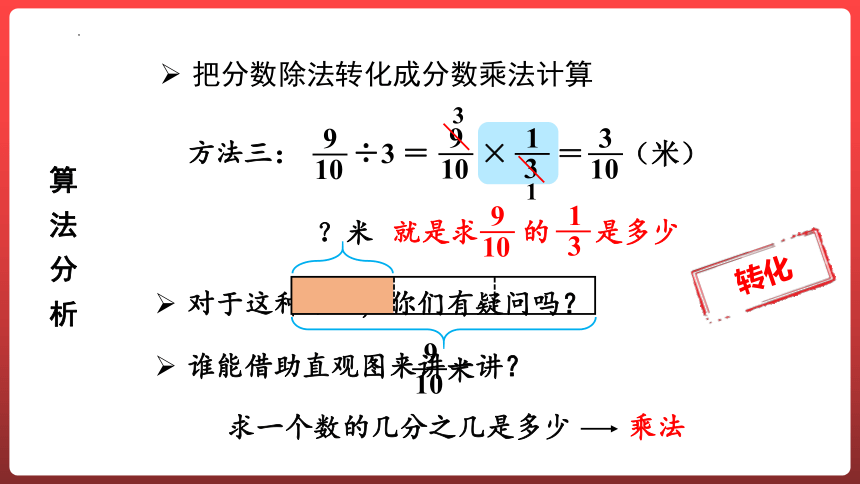
把分数除法转化成分数乘法计算
9
10
÷3
=
方法三:
=
3
10
(米)
9
10
×
1
3
3
1
9
10
米
?米
就是求 的 是多少
9
10
1
3
求一个数的几分之几是多少
乘法
转化
知识回顾
5
3
×
4
3
5
1
×
2
1
数
形
结
合
用 米布料可以做2条裤子,做一条裤子需要布料多少米?
6
5
先列出算式,再选择前面的方法算一算。
你选择的方法能得出正确答案吗?为什么?
小组内交流你的算法。
自主探究
用 米布料可以做2条裤子,做一条裤子需要布料多少米?
6
5
5
6
÷2
把分数转化成小数计算
这种方法可以用吗?为什么?
用 米布料可以做2条裤子,做一条裤子需要布料多少米?
6
5
5
6
÷2
根据平均分的含义计算
5
6
÷2
=
5÷2
6
=
2.5
6
=
25
60
=
5
12
(米)
太麻烦
用 米布料可以做2条裤子,做一条裤子需要布料多少米?
6
5
5
6
÷2
把分数除法转化成分数乘法计算
5
6
÷2
=
=
5
12
(米)
5
6
×
1
2
对比分析这三种方法,你们有什么发现?
同桌合作
局限性
普遍性
4
5
÷3
8
9
÷4
4
5
÷3
=
4
15
4
5
×
1
3
=
8
9
÷4
=
2
9
8
9
×
1
4
=
2
1
说一说,你是怎样计算的?
9
10
÷3
=
=
3
10
9
10
×
1
3
3
1
5
6
÷2
=
=
5
12
5
6
×
1
2
4
5
÷3
=
4
15
4
5
×
1
3
=
8
9
÷4
=
2
9
8
9
×
1
4
=
2
1
你能用一句话概括如何计算分数除以整数吗?
观察这四个算式,它们在计算时有什么共同的特点?
分数除以整数,等于分数乘这个整数的倒数。
等于分数乘这个整数的倒数。
(0除外),
,
分数除以整数
0也是整数,可以除以0吗?
你认为哪里比较容易出错,需要注意?
1.算一算。
÷6=
3
4
12
17
4
5
2
17
2
15
1
8
12
17
÷6
=
12÷6
17
=
2
17
12
17
÷6
=
=
2
17
12
17
×
1
6
2
1
2.火眼金睛辨对错。
(1)
8
15
÷5
=
8
15÷5
=
8
3
(2)
3
9
÷3
=
3÷3
9÷3
=
1
3
(3)如果a是不等于0的自然数,那么
1
5
÷a
=
1
a
1
5
÷ 。
( )
( )
( )
×
×
×
3.平均每个桃子重多少千克?
5
8
千克
5
8
÷5
=
5÷5
8
=
1
8
(千克)
5
8
÷5
=
=
1
8
5
8
×
1
5
1
1
(千克)
答:平均每个桃子重 千克。
1
8
或
依据情景,提出问题
应用算法,巩固练习
探究算法,解决问题
自主优化,总结算法
3.1.分数除以整数
5
1
×
2
1
=
5
3
×
4
3
=
7
4
×
5
3
=
8
5
×
5
3
=
10
1
35
12
20
9
8
3
回顾一下,我们是怎样学习分数乘法的?
布艺兴趣小组用 米布料给小猴做背心,可以做3件;用 米布料做裤子,可以做2条。
9
10
5
6
阅读题目,想一想你能提出哪些数学问题?
做一件背心需要布料多少米?
做一条裤子需要布料多少米?
用 米布料可以做3件背心,做一件背心需要布料多少米?
10
9
怎样列式?为什么这样列式?
10
9
÷ 3
平均分
仔细观察这个算式,找一找与我们以前学习过的除法算式有哪些地方相同,哪些地方不同?
同桌合作
分数除以整数
想一想:能利用以前学过的知识计算 吗?
做一做:把你的想法写在练习本上。
说一说:在小组内交流你的计算方法。
评一评:小组成员对每种算法进行评价、质疑。
自主探究
10
9
÷3
算法展示
9
10
÷3
=0.9÷3=0.3(米)
方法一:
9
10
÷3
=
方法二:
9÷3
10
=
3
10
(米)
9
10
÷3
=
方法三:
=
3
10
(米)
9
10
×
1
3
3
1
仔细观察,你的方法与哪种方法相同?你能看懂这些方法吗?
算法
分
析
9
10
÷3
=0.9÷3=0.3(米)
方法一:
你是怎样想的?为什么要把它化成小数?
运用了哪种常用的数学方法?
把分数转化成小数计算
分数除以整数
小数除法
转化
算法
分
析
为什么这样算?这样算的依据是什么?
谁能借助直观图来讲一讲?
根据平均分的含义计算
9
10
÷3
=
方法二:
9÷3
10
=
3
10
(米)
1米
3
10
9
10
3
10
3
10
还有不同的画图方法吗?
米
米
米
米
算法
分
析
对于这种方法,你们有疑问吗?
谁能借助直观图来讲一讲?
把分数除法转化成分数乘法计算
9
10
÷3
=
方法三:
=
3
10
(米)
9
10
×
1
3
3
1
9
10
米
?米
就是求 的 是多少
9
10
1
3
求一个数的几分之几是多少
乘法
转化
知识回顾
5
3
×
4
3
5
1
×
2
1
数
形
结
合
用 米布料可以做2条裤子,做一条裤子需要布料多少米?
6
5
先列出算式,再选择前面的方法算一算。
你选择的方法能得出正确答案吗?为什么?
小组内交流你的算法。
自主探究
用 米布料可以做2条裤子,做一条裤子需要布料多少米?
6
5
5
6
÷2
把分数转化成小数计算
这种方法可以用吗?为什么?
用 米布料可以做2条裤子,做一条裤子需要布料多少米?
6
5
5
6
÷2
根据平均分的含义计算
5
6
÷2
=
5÷2
6
=
2.5
6
=
25
60
=
5
12
(米)
太麻烦
用 米布料可以做2条裤子,做一条裤子需要布料多少米?
6
5
5
6
÷2
把分数除法转化成分数乘法计算
5
6
÷2
=
=
5
12
(米)
5
6
×
1
2
对比分析这三种方法,你们有什么发现?
同桌合作
局限性
普遍性
4
5
÷3
8
9
÷4
4
5
÷3
=
4
15
4
5
×
1
3
=
8
9
÷4
=
2
9
8
9
×
1
4
=
2
1
说一说,你是怎样计算的?
9
10
÷3
=
=
3
10
9
10
×
1
3
3
1
5
6
÷2
=
=
5
12
5
6
×
1
2
4
5
÷3
=
4
15
4
5
×
1
3
=
8
9
÷4
=
2
9
8
9
×
1
4
=
2
1
你能用一句话概括如何计算分数除以整数吗?
观察这四个算式,它们在计算时有什么共同的特点?
分数除以整数,等于分数乘这个整数的倒数。
等于分数乘这个整数的倒数。
(0除外),
,
分数除以整数
0也是整数,可以除以0吗?
你认为哪里比较容易出错,需要注意?
1.算一算。
÷6=
3
4
12
17
4
5
2
17
2
15
1
8
12
17
÷6
=
12÷6
17
=
2
17
12
17
÷6
=
=
2
17
12
17
×
1
6
2
1
2.火眼金睛辨对错。
(1)
8
15
÷5
=
8
15÷5
=
8
3
(2)
3
9
÷3
=
3÷3
9÷3
=
1
3
(3)如果a是不等于0的自然数,那么
1
5
÷a
=
1
a
1
5
÷ 。
( )
( )
( )
×
×
×
3.平均每个桃子重多少千克?
5
8
千克
5
8
÷5
=
5÷5
8
=
1
8
(千克)
5
8
÷5
=
=
1
8
5
8
×
1
5
1
1
(千克)
答:平均每个桃子重 千克。
1
8
或
依据情景,提出问题
应用算法,巩固练习
探究算法,解决问题
自主优化,总结算法
