1.5.倒数(课件)-六年级上册数学青岛版(共13张PPT)
文档属性
| 名称 | 1.5.倒数(课件)-六年级上册数学青岛版(共13张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 500.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 09:36:50 | ||
图片预览




文档简介
(共13张PPT)
1.5.倒数
6
5
×
5
6
=
11
7
×
7
11
=
5
1
×
5
=
19
1
×
19
=
5
2
×
4
1
=
4
3
×
6
=
计算下面各题。
独立计算,回顾旧知
学生独立完成上面的几组题目,小组内检查并订正。
说一说分数乘法的计算方法,突出分子与分母的约分。
算式分类,关注特点
观察算式,可将它们分成哪两类,说一说理由。
观察每一类算式的特点,说出自己的发现。
举例验证你的发现。
6
5
×
5
6
=
11
7
×
7
11
=
5
1
×
5
=
19
1
×
19
=
5
2
×
4
1
=
4
3
×
6
=
1
1
1
1
10
1
2
9
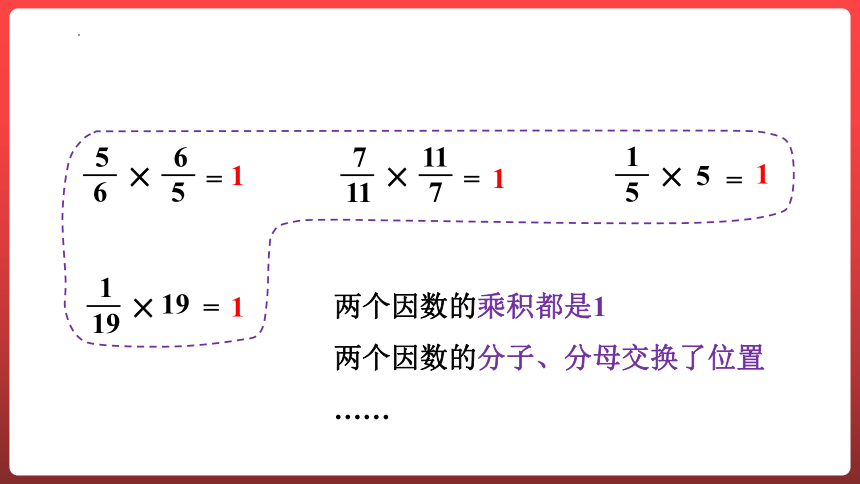
两个因数的乘积都是1
两个因数的分子、分母交换了位置
……
4
3
×
3
4
=
12
5
×
5
12
=
7
1
×
7
=
1
1
1
100
1
×
100
=
1
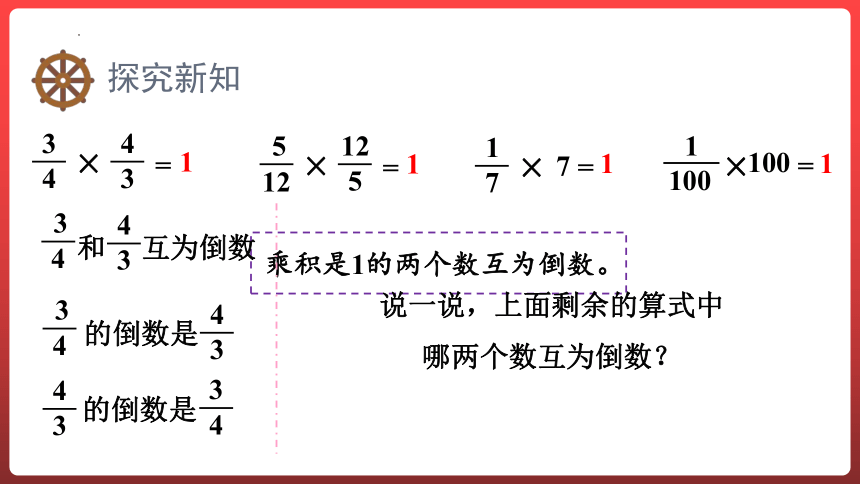
乘积是1的两个数互为倒数。
4
3
和
3
4
互为倒数
4
3
的倒数是
3
4
3
4
的倒数是
4
3
说一说,上面剩余的算式中
哪两个数互为倒数?
乘积是1的两个数互为倒数。
说一说自己对倒数的理解。
互为倒数的两个数有什么特点?
两个数的分子、分母交换位置,如果一个数大于1,另一个数一定小于1
不能孤立地说某个数是倒数,倒数是相互依存的
将互为倒数的两个数连起来。
7
3
6
2
5
17
16
13
18
6
1
16
17
18
13
5
2
3
7
写出下面各数的倒数。
2
1
9
2
5
7
4
你能很快地说出上面各数的倒数吗?说一说你是怎么想的?
小组讨论:如何求整数、小数的倒数?
1的倒数是多少?0有倒数吗?
2
1
9
2
5
7
4
1
2
= 2
=
1
4
整数可以看成分母是1的分数
2
9
7
5
4
1
求一个分数的倒数,直接将分子分母交换位置即可。
0.2
5
1
=
1
5
= 5
小数
化为分数
找倒数
如何求小数的倒数?
1.2
5
6
=
6
5
1的倒数是多少?0有倒数吗?
1
0
×1 = 1
1的倒数是它本身
× = 1
×任何数= 0
0没有倒数
(2)因为1的倒数是1,所以0的倒数是0。 ( )
(3)所有的真分数的倒数都比1大。 ( )
7
2
×
2
7
=1,所以 是倒数。 ( )
2
7
(1)
火眼金睛辨对错。
×
×
√
7
2
和 互为倒数
2
7
0没有倒数
独立计算,初步感知
逐层深入,认识倒数
交流探讨,会求倒数
1.5.倒数
6
5
×
5
6
=
11
7
×
7
11
=
5
1
×
5
=
19
1
×
19
=
5
2
×
4
1
=
4
3
×
6
=
计算下面各题。
独立计算,回顾旧知
学生独立完成上面的几组题目,小组内检查并订正。
说一说分数乘法的计算方法,突出分子与分母的约分。
算式分类,关注特点
观察算式,可将它们分成哪两类,说一说理由。
观察每一类算式的特点,说出自己的发现。
举例验证你的发现。
6
5
×
5
6
=
11
7
×
7
11
=
5
1
×
5
=
19
1
×
19
=
5
2
×
4
1
=
4
3
×
6
=
1
1
1
1
10
1
2
9
两个因数的乘积都是1
两个因数的分子、分母交换了位置
……
4
3
×
3
4
=
12
5
×
5
12
=
7
1
×
7
=
1
1
1
100
1
×
100
=
1
乘积是1的两个数互为倒数。
4
3
和
3
4
互为倒数
4
3
的倒数是
3
4
3
4
的倒数是
4
3
说一说,上面剩余的算式中
哪两个数互为倒数?
乘积是1的两个数互为倒数。
说一说自己对倒数的理解。
互为倒数的两个数有什么特点?
两个数的分子、分母交换位置,如果一个数大于1,另一个数一定小于1
不能孤立地说某个数是倒数,倒数是相互依存的
将互为倒数的两个数连起来。
7
3
6
2
5
17
16
13
18
6
1
16
17
18
13
5
2
3
7
写出下面各数的倒数。
2
1
9
2
5
7
4
你能很快地说出上面各数的倒数吗?说一说你是怎么想的?
小组讨论:如何求整数、小数的倒数?
1的倒数是多少?0有倒数吗?
2
1
9
2
5
7
4
1
2
= 2
=
1
4
整数可以看成分母是1的分数
2
9
7
5
4
1
求一个分数的倒数,直接将分子分母交换位置即可。
0.2
5
1
=
1
5
= 5
小数
化为分数
找倒数
如何求小数的倒数?
1.2
5
6
=
6
5
1的倒数是多少?0有倒数吗?
1
0
×1 = 1
1的倒数是它本身
× = 1
×任何数= 0
0没有倒数
(2)因为1的倒数是1,所以0的倒数是0。 ( )
(3)所有的真分数的倒数都比1大。 ( )
7
2
×
2
7
=1,所以 是倒数。 ( )
2
7
(1)
火眼金睛辨对错。
×
×
√
7
2
和 互为倒数
2
7
0没有倒数
独立计算,初步感知
逐层深入,认识倒数
交流探讨,会求倒数
