相似三角形的应用[下学期]
文档属性
| 名称 | 相似三角形的应用[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 16.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-09-25 20:00:00 | ||
图片预览

文档简介
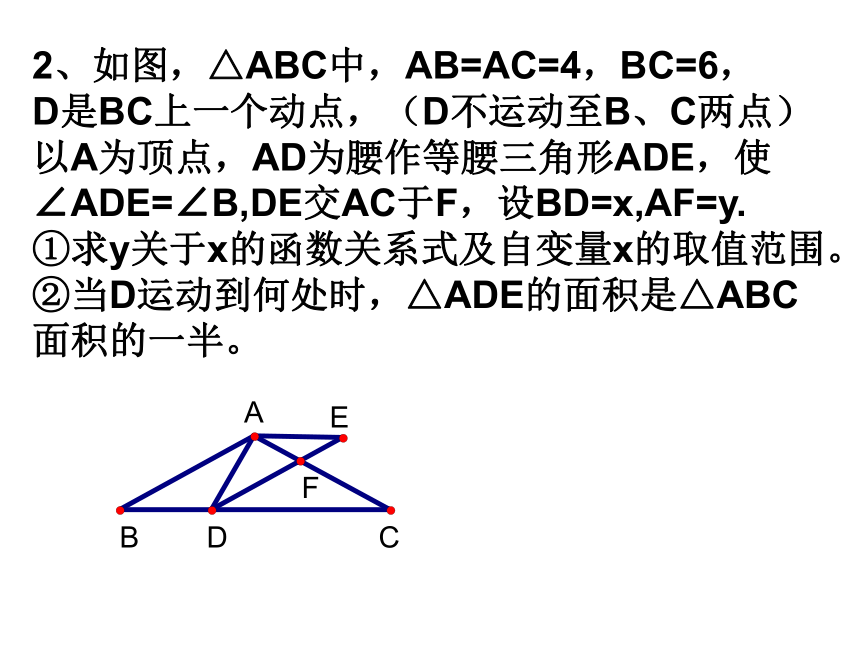
课件8张PPT。1、如图,在△ABC和△A’B’C’中,∠A=∠A’
=900,AB=A’B’=4,AC=2A’C’=6。
(1)判断这两个直角三角形相似吗?说明理由。
(2)能否分别作一条辅助线将这两个三角形分
割,使△ABC分割成的两个△与△A’B’C’分割成
的两个△分别对应相似?请设计分割方案,并加
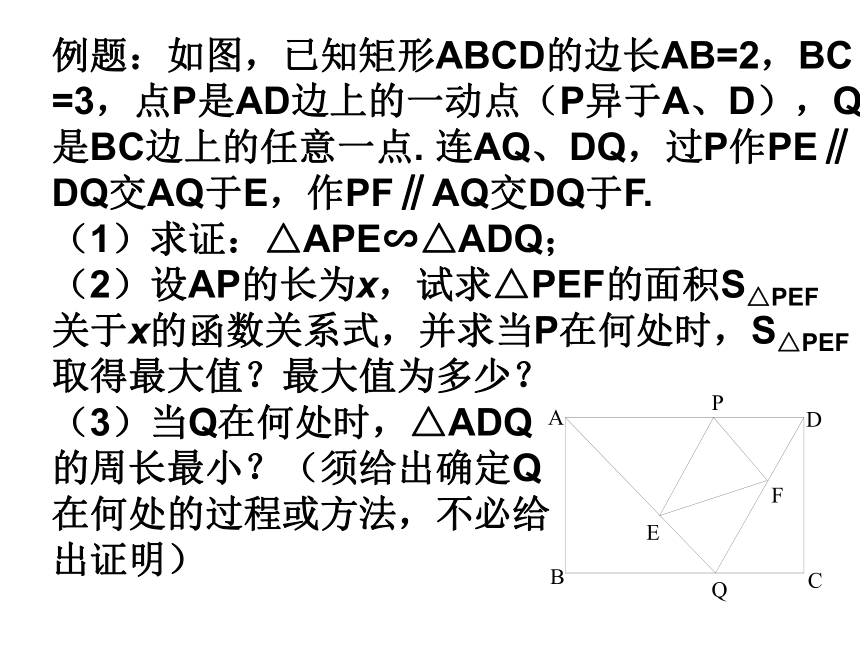
以说明。AA’C’B’CB2、如图,△ABC中,AB=AC=4,BC=6,
D是BC上一个动点,(D不运动至B、C两点)
以A为顶点,AD为腰作等腰三角形ADE,使
∠ADE=∠B,DE交AC于F,设BD=x,AF=y.
①求y关于x的函数关系式及自变量x的取值范围。
②当D运动到何处时,△ADE的面积是△ABC
面积的一半。例题:如图,已知矩形ABCD的边长AB=2,BC
=3,点P是AD边上的一动点(P异于A、D),Q
是BC边上的任意一点. 连AQ、DQ,过P作PE∥
DQ交AQ于E,作PF∥AQ交DQ于F.
(1)求证:△APE∽△ADQ;
(2)设AP的长为x,试求△PEF的面积S△PEF
关于x的函数关系式,并求当P在何处时,S△PEF
取得最大值?最大值为多少?
(3)当Q在何处时,△ADQ
的周长最小?(须给出确定Q
在何处的过程或方法,不必给
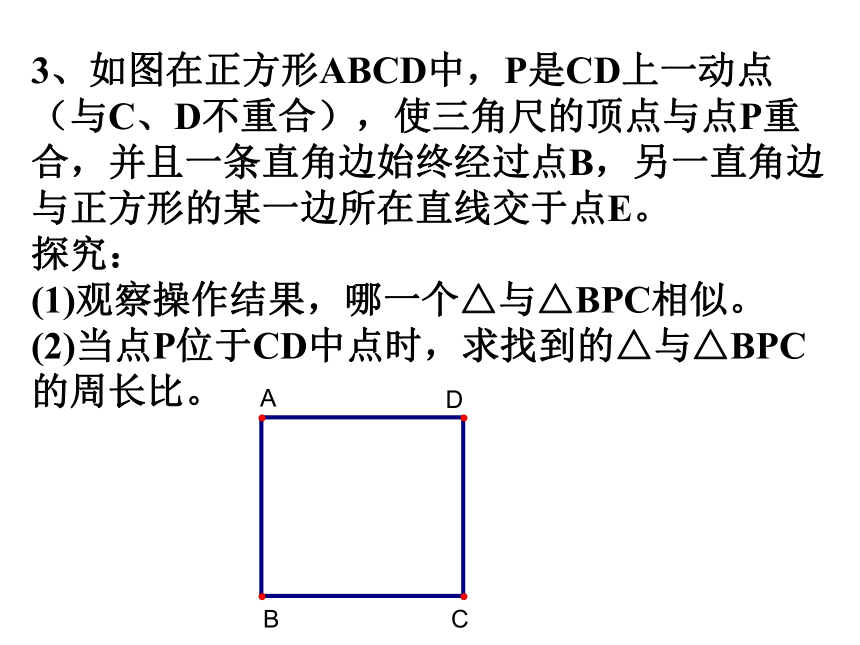
出证明)3、如图在正方形ABCD中,P是CD上一动点
(与C、D不重合),使三角尺的顶点与点P重
合,并且一条直角边始终经过点B,另一直角边
与正方形的某一边所在直线交于点E。
探究:
(1)观察操作结果,哪一个△与△BPC相似。
(2)当点P位于CD中点时,求找到的△与△BPC
的周长比。4、如图,在△ABC中,AB=5,BC=3,AC=4,PQ
∥点P在AC上(与点A、C不重合),点Q在BC上。
(1)当△PQC的面积与四边形PABQ面积相等时,
求CP的长。
(2)当△PQC的周长与四边形PABQ的周长相等
时,求CP?
(3)试问在AB上是否存在点M,使得△PQM是
等腰Rt三角形?若不存在,请说明理由;若存在,
请求出PQ的长.5、如图所示,在△ABC中,BA=BC=20,AC
=30,点P从点A出发,沿着AB以每秒4cm的速
度向B点运动,同时,点Q从C点出发,沿着CA
以每秒3cm的速度向A点运动,设运动时间为x,
(1)当x为何值时,PQ∥BC。
(2)
(3)△APQ能否与△CQB相似?若能,求AP的长。7、如图已知∠AOB=900,OM是∠AOB的角平
分线,按下列要求回答:
(1)将三角板的直角顶点P在射线OM上移动,两
直角边分别与边OA=OB交于点C、D。
①在图中,证明:PC=PD.
②在图(2)中,点G是CD与OP的交点,且PG=
PD,求△POD与△PDG的面积比。
(2)将△的直角顶点P在射线OM上移动,一直角边
与边OB交于点D,OD=1,另一直角边与直线O
A,直线OB分别交于点C、E,使以P、D、E为
顶点的△与△OCD相似,在图中作出图形,试求
OP的长。
=900,AB=A’B’=4,AC=2A’C’=6。
(1)判断这两个直角三角形相似吗?说明理由。
(2)能否分别作一条辅助线将这两个三角形分
割,使△ABC分割成的两个△与△A’B’C’分割成
的两个△分别对应相似?请设计分割方案,并加
以说明。AA’C’B’CB2、如图,△ABC中,AB=AC=4,BC=6,
D是BC上一个动点,(D不运动至B、C两点)
以A为顶点,AD为腰作等腰三角形ADE,使
∠ADE=∠B,DE交AC于F,设BD=x,AF=y.
①求y关于x的函数关系式及自变量x的取值范围。
②当D运动到何处时,△ADE的面积是△ABC
面积的一半。例题:如图,已知矩形ABCD的边长AB=2,BC
=3,点P是AD边上的一动点(P异于A、D),Q
是BC边上的任意一点. 连AQ、DQ,过P作PE∥
DQ交AQ于E,作PF∥AQ交DQ于F.
(1)求证:△APE∽△ADQ;
(2)设AP的长为x,试求△PEF的面积S△PEF
关于x的函数关系式,并求当P在何处时,S△PEF
取得最大值?最大值为多少?
(3)当Q在何处时,△ADQ
的周长最小?(须给出确定Q
在何处的过程或方法,不必给
出证明)3、如图在正方形ABCD中,P是CD上一动点
(与C、D不重合),使三角尺的顶点与点P重
合,并且一条直角边始终经过点B,另一直角边
与正方形的某一边所在直线交于点E。
探究:
(1)观察操作结果,哪一个△与△BPC相似。
(2)当点P位于CD中点时,求找到的△与△BPC
的周长比。4、如图,在△ABC中,AB=5,BC=3,AC=4,PQ
∥点P在AC上(与点A、C不重合),点Q在BC上。
(1)当△PQC的面积与四边形PABQ面积相等时,
求CP的长。
(2)当△PQC的周长与四边形PABQ的周长相等
时,求CP?
(3)试问在AB上是否存在点M,使得△PQM是
等腰Rt三角形?若不存在,请说明理由;若存在,
请求出PQ的长.5、如图所示,在△ABC中,BA=BC=20,AC
=30,点P从点A出发,沿着AB以每秒4cm的速
度向B点运动,同时,点Q从C点出发,沿着CA
以每秒3cm的速度向A点运动,设运动时间为x,
(1)当x为何值时,PQ∥BC。
(2)
(3)△APQ能否与△CQB相似?若能,求AP的长。7、如图已知∠AOB=900,OM是∠AOB的角平
分线,按下列要求回答:
(1)将三角板的直角顶点P在射线OM上移动,两
直角边分别与边OA=OB交于点C、D。
①在图中,证明:PC=PD.
②在图(2)中,点G是CD与OP的交点,且PG=
PD,求△POD与△PDG的面积比。
(2)将△的直角顶点P在射线OM上移动,一直角边
与边OB交于点D,OD=1,另一直角边与直线O
A,直线OB分别交于点C、E,使以P、D、E为
顶点的△与△OCD相似,在图中作出图形,试求
OP的长。
