人教版数学五年级上册 第5单元 简易方程-实际问题与方程例1课件(共16张PPT)
文档属性
| 名称 | 人教版数学五年级上册 第5单元 简易方程-实际问题与方程例1课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
简易方程
实际问题与方程(例1)
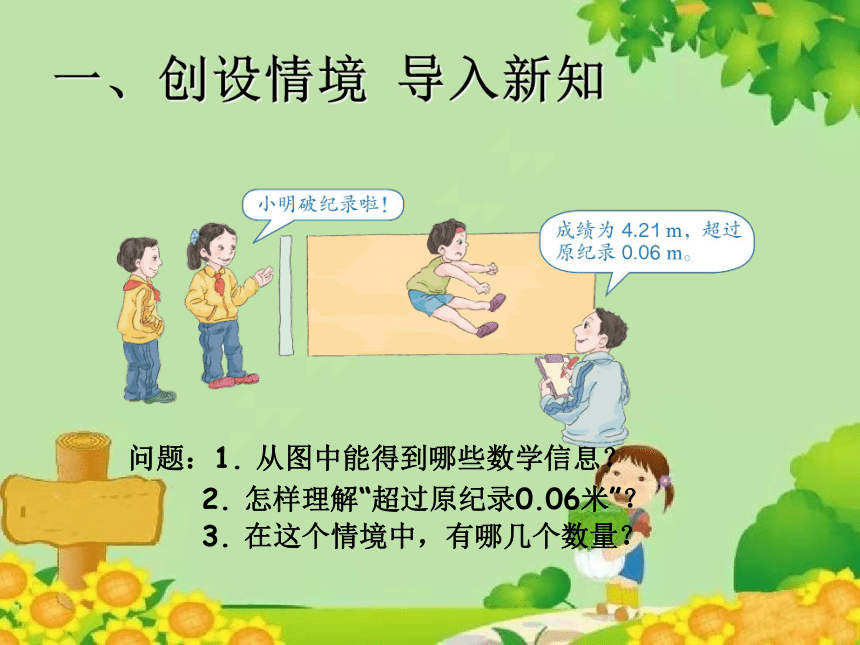
问题:1. 从图中能得到哪些数学信息?
2. 怎样理解“超过原纪录0.06米”?
一、创设情境 导入新知
3. 在这个情境中,有哪几个数量?
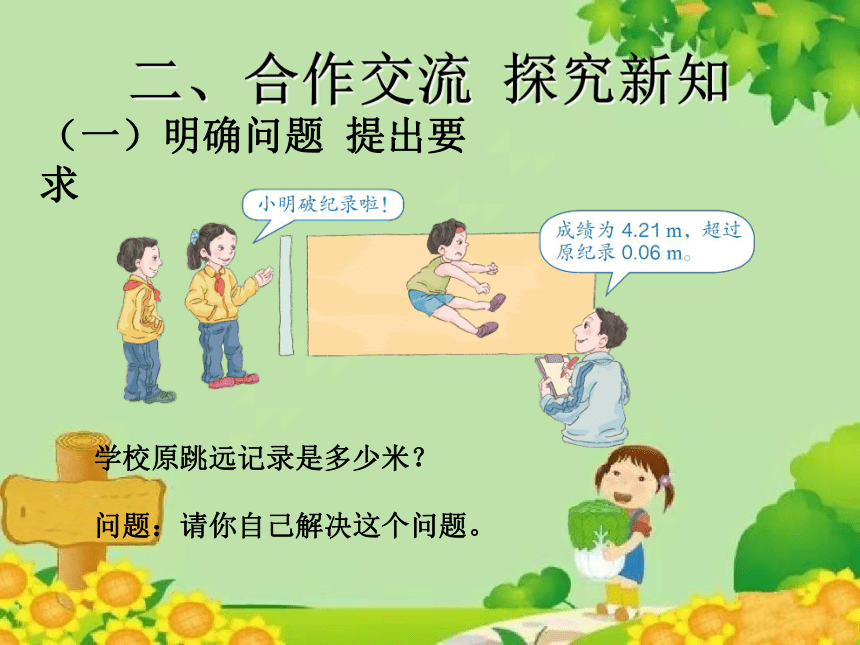
二、合作交流 探究新知
问题:请你自己解决这个问题。
(一)明确问题 提出要求
学校原跳远记录是多少米?
二、合作交流 探究新知
(二)暴露思维 组织研讨
4.21米
0.06米
?米
原纪录
小明
预设1:
4.21-0.06=4.15(m)
2. 他的解答正确吗?
问题:1. 请说说你的想法。
二、合作交流 探究新知
(二)暴露思维 组织研讨
解:设学校原跳远纪录是x米。
x+0.06=4.21 x+0.06-0.06=4.21-0.06 x=4.15
原纪录+超出部分=小明的成绩
答:学校原跳远纪录是4.15米。
2. 他的解答正确吗?
问题:1. 请说说你的想法。
预设2:
二、合作交流 探究新知
(二)暴露思维 组织研讨
解:设学校原跳远纪录是x米。
预设3:
4.21-x=0.06 4.21-x+x =0.06+x
4.21=0.06+x 0.06+x=4.21 0.06+x-0.06=4.21-0.06 x=4.15
监控:(1)把结果代入原方程,看看左右两边是否相等。 (2)把所求出来的结果作为已知条件,题目中的一个已知条件变为未 知条件,再重新做一遍。
2. 他的解答正确吗?
问题:1. 看看这位同学列的方程,你能读懂他的想法吗?
小明的成绩-原纪录=超出部分
2. 用方程的思路解决问题,你认为关键是什么?
问题:1. 同一个问题,我们用了几种不同的方法解决?都合理吗?
(可以用算术的方法,也可以列方程解答。)
二、合作交流 探究新知
(三)沟通联系 提升认识
(找出等量关系)
3. 方程解法与算术解法有什么区别
(列方程解决问题时,未知数用字母表示,参与列式;
算术方法中未知数不参与列式。)
三、巩固新知 拓展应用
问题:你能用方程解决这个问题吗?自己试着做一做。
1.
小明去年身高多少?
三、巩固新知 拓展应用
问题:1. 请说一说你的想法。
解:设小明去年身高x米。
0.08+x=1.53
0.08+x-x=1.53-x
x=1.45
2. 解决这个问题时,你想提醒大家注意什么呢?(统一单位)
答:小明去年身高1.45米。
8cm=0.08m
预设1:
解:设小明去年身高x米。
8cm=0.08m
预设2:
1.53-x=0.08 1.53-x+x=0.08+x
1.53=0.08+x 0.08+x=1.53 0.08+x-0.08=1.53-0.08 x=1.45
三、巩固新知 拓展应用
问题:你能用方程解决这个问题吗?自己试着做一做。
2.
三、巩固新知 拓展应用
解:设一个滴水的水龙头每分钟浪费x千克水。
x=0.06
答:一个滴水的水龙头每分钟浪费0.06千克水。
半小时=30分
30x=1.8
每分钟滴的水×30=半小时滴的水
30x÷30=1.8÷30
问题:1. 这位同学的想法你能看懂吗?
预设1:
2. 解决这个问题时,你想提醒大家注意什么呢?
三、巩固新知 拓展应用
半小时滴的水÷每分钟滴的水=30
解:设一个滴水的水龙头每分钟浪费x千克水。
问题:1. 请说一说你的想法。
2. 解决这个问题时,你想提醒大家注意什么呢?
1.8÷x=30 1.8÷x×x=30×x 1.8=30x 30x=1.8 30x÷30=1.8÷30 x=0.06
预设2:
四、全课总结
今天都有哪些收获?还有什么问题?
再见
GOODBYE
谢 谢 大 家
简易方程
实际问题与方程(例1)
问题:1. 从图中能得到哪些数学信息?
2. 怎样理解“超过原纪录0.06米”?
一、创设情境 导入新知
3. 在这个情境中,有哪几个数量?
二、合作交流 探究新知
问题:请你自己解决这个问题。
(一)明确问题 提出要求
学校原跳远记录是多少米?
二、合作交流 探究新知
(二)暴露思维 组织研讨
4.21米
0.06米
?米
原纪录
小明
预设1:
4.21-0.06=4.15(m)
2. 他的解答正确吗?
问题:1. 请说说你的想法。
二、合作交流 探究新知
(二)暴露思维 组织研讨
解:设学校原跳远纪录是x米。
x+0.06=4.21 x+0.06-0.06=4.21-0.06 x=4.15
原纪录+超出部分=小明的成绩
答:学校原跳远纪录是4.15米。
2. 他的解答正确吗?
问题:1. 请说说你的想法。
预设2:
二、合作交流 探究新知
(二)暴露思维 组织研讨
解:设学校原跳远纪录是x米。
预设3:
4.21-x=0.06 4.21-x+x =0.06+x
4.21=0.06+x 0.06+x=4.21 0.06+x-0.06=4.21-0.06 x=4.15
监控:(1)把结果代入原方程,看看左右两边是否相等。 (2)把所求出来的结果作为已知条件,题目中的一个已知条件变为未 知条件,再重新做一遍。
2. 他的解答正确吗?
问题:1. 看看这位同学列的方程,你能读懂他的想法吗?
小明的成绩-原纪录=超出部分
2. 用方程的思路解决问题,你认为关键是什么?
问题:1. 同一个问题,我们用了几种不同的方法解决?都合理吗?
(可以用算术的方法,也可以列方程解答。)
二、合作交流 探究新知
(三)沟通联系 提升认识
(找出等量关系)
3. 方程解法与算术解法有什么区别
(列方程解决问题时,未知数用字母表示,参与列式;
算术方法中未知数不参与列式。)
三、巩固新知 拓展应用
问题:你能用方程解决这个问题吗?自己试着做一做。
1.
小明去年身高多少?
三、巩固新知 拓展应用
问题:1. 请说一说你的想法。
解:设小明去年身高x米。
0.08+x=1.53
0.08+x-x=1.53-x
x=1.45
2. 解决这个问题时,你想提醒大家注意什么呢?(统一单位)
答:小明去年身高1.45米。
8cm=0.08m
预设1:
解:设小明去年身高x米。
8cm=0.08m
预设2:
1.53-x=0.08 1.53-x+x=0.08+x
1.53=0.08+x 0.08+x=1.53 0.08+x-0.08=1.53-0.08 x=1.45
三、巩固新知 拓展应用
问题:你能用方程解决这个问题吗?自己试着做一做。
2.
三、巩固新知 拓展应用
解:设一个滴水的水龙头每分钟浪费x千克水。
x=0.06
答:一个滴水的水龙头每分钟浪费0.06千克水。
半小时=30分
30x=1.8
每分钟滴的水×30=半小时滴的水
30x÷30=1.8÷30
问题:1. 这位同学的想法你能看懂吗?
预设1:
2. 解决这个问题时,你想提醒大家注意什么呢?
三、巩固新知 拓展应用
半小时滴的水÷每分钟滴的水=30
解:设一个滴水的水龙头每分钟浪费x千克水。
问题:1. 请说一说你的想法。
2. 解决这个问题时,你想提醒大家注意什么呢?
1.8÷x=30 1.8÷x×x=30×x 1.8=30x 30x=1.8 30x÷30=1.8÷30 x=0.06
预设2:
四、全课总结
今天都有哪些收获?还有什么问题?
再见
GOODBYE
谢 谢 大 家
