人教A版(2019)数学必修第一册 3.3幂函数课件(共33张PPT)
文档属性
| 名称 | 人教A版(2019)数学必修第一册 3.3幂函数课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 00:00:00 | ||
图片预览










文档简介
(共33张PPT)
幂函数
1.了解幂函数的概念,会求幂函数的解析式.
2.结合y=x,y=x2,y=x3,y= ,y=x-1的图象,了解它们的变化情况.
3.能利用幂函数的单调性比较指数幂的大小.
本节目标
课前预习
(1)幂函数是如何定义的?
(2)幂函数的解析式具有什么特点?
(3)常见幂函数的图象是什么?它具有哪些性质?
预习课本P89~91,思考并完成以下问题
课前小测
1.下列函数中不是幂函数的是( )
A.y= B.y=x3
C.y=3x D.y=x-1
C
不符合幂函数y=xα的形式
2.已知f(x)=(m+1) 是幂函数,则m=( )
A.2 B.1 C.3 D.0
m+1=1,即m=0
D
3.已知幂函数f(x)=xα的图象过点,则f(4)=________.
f(2)=
2α=
α=-
f(4)= =
新知探究
1.幂函数的概念
一般地,函数_________叫做幂函数,其中____是自变量,_____是常数.
y=xα
x
α
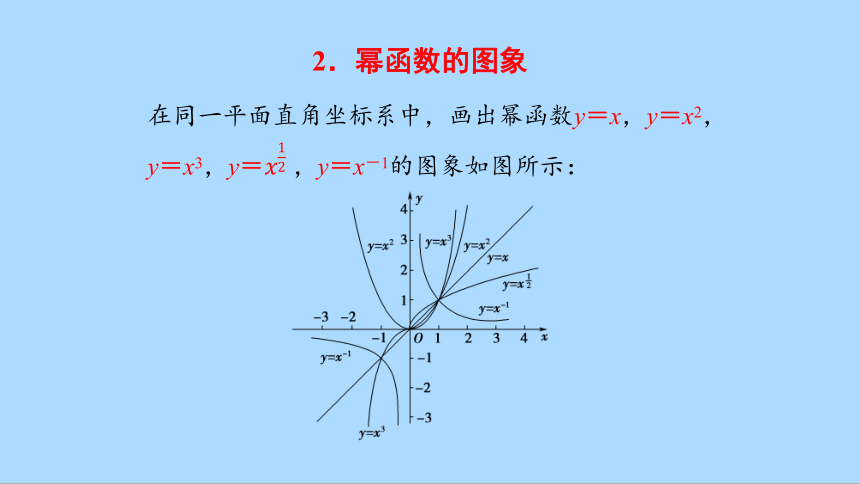
2.幂函数的图象
在同一平面直角坐标系中,画出幂函数y=x,y=x2,y=x3,y=,y=x-1的图象如图所示:
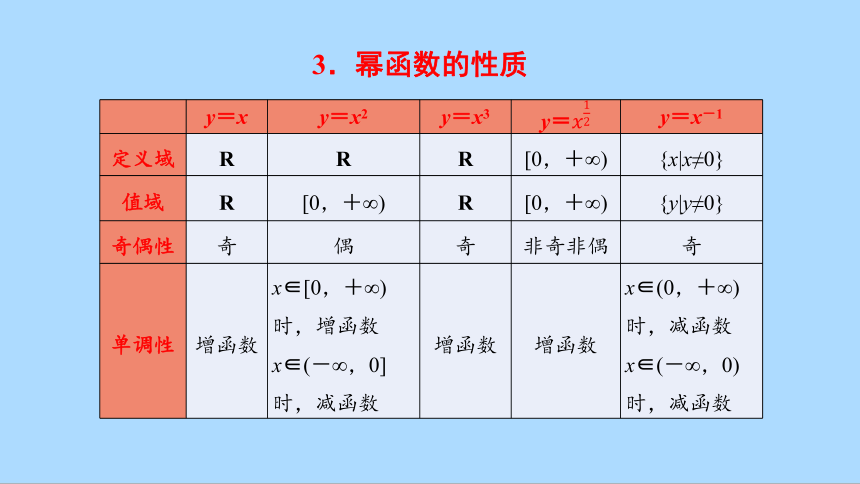
3.幂函数的性质
y=x y=x2 y=x3 y= y=x-1
定义域 R R R [0,+∞) {x|x≠0}
值域 R [0,+∞) R [0,+∞) {y|y≠0}
奇偶性 奇 偶 奇 非奇非偶 奇
单调性 增函数 x∈[0,+∞) 时,增函数 x∈(-∞,0] 时,减函数 增函数 增函数 x∈(0,+∞)
时,减函数
x∈(-∞,0)
时,减函数
题型突破
典例深度剖析 重点多维探究
题型一 幂函数的概念
[例1] 已知y=(m2+2m-2) +2n-3是幂函数,求m,n的值.
所以m=-3,n= .
由题意得
解得
判断一个函数是否为幂函数的依据是该函数是否为y=xα α为常数 的形式,即函数的解析式为一个幂的形式,且需满足:
1 指数为常数;
2 底数为自变量;
3 系数为1.
判断一个函数是否为幂函数的方法
方法总结
1.在函数y=,y=2x2,y=x2+x,y=1中,幂函数的个数为( )
A.0 B.1
C.2 D.3
跟踪训练
B
√
×
×
×
题型二 幂函数的图象及应用
[例2] 点(,2)与点分别在幂函数f(x),g(x)的图象上,问当x为何值时,有:
(1)f(x)>g(x); (2)f(x)=g(x); (3)f(x)[例2] 点(,2)与点分别在幂函数f(x),g(x)的图象上,问当x为何值时,有:
(1)f(x)>g(x); (2)f(x)=g(x); (3)f(x)设f(x)=xα,g(x)=xβ.
∵()α=2,(-2)β=- ,
∴α=2,β=-1,
∴f(x)=x2,g(x)=x-1.
分别作出它们的图象,如图所示.
[例2] 点(,2)与点分别在幂函数f(x),g(x)的图象上,问当x为何值时,有:
(1)f(x)>g(x); (2)f(x)=g(x); (3)f(x)由图象知,
(1) 当x∈(-∞,0)∪(1,+∞)时,f(x)>g(x);
(2) 当x=1时,f(x)=g(x);
(3) 当x∈(0,1)时,f(x)① 依据图象高低判断幂指数大小,相关结论为
在 0,1 上,指数越大,幂函数图象越靠近x轴 简记为指大图低 ;
在 1,+∞ 上,指数越大,幂函数图象越远离x轴 简记为指大图高 .
解决幂函数图象问题应把握的两个原则
②依据图象确定幂指数α与0,1的大小关系,即根据幂函数在第一象限内的图象 类似于y=x-1或y=或y=x3 来判断.
方法总结
2. (1)若四个幂函数y=xa,y=xb,y=xc,y=xd在同一坐标系中的图象如图,则a,b,c,d的大小关系是( )
A.d>c>b>a B.a>b>c>d
C.d>c>a>b D.a>b>d>c
跟踪训练
B
(2)函数y=-1的图象关于x轴对称的图象大致是( )
A B C D
B
y=的图象位于第一象限且为增函数,所以函数图象是上升的
y=-1的图象可看作由y=的图象向下平移一个单位得到的(如选项A中的图所示)
将y=-1的图象关于x轴对称后即为选项B
题型三 幂函数性质的综合应用
[探究问题]
1.幂函数y=xα在(0,+∞)上的单调性与α有什么关系?
提示:
当α>0时,幂函数y=xα在(0,+∞)上单调递增;当α<0时,幂函数y=xα在(0,+∞)上单调递减.
2.2.3-0.2和2.2-0.2可以看作哪一个函数的两个函数值?二者的大小关系如何?
提示:
2.3-0.2和2.2-0.2可以看作幂函数f(x)=x-0.2的两个函数值,因为函数f(x)=x-0.2在(0,+∞)上单调递减,所以2.3-0.2<2.2-0.2.
[探究问题]
[例3] 比较下列各组中幂值的大小:
(1) 0.213, 0.233; (2) , , .
∵函数y=x3是增函数,且0.21<0.23,
∴0.213<0.233.
[例3] 比较下列各组中幂值的大小:
(1) 0.213, 0.233; (2) , , .
= , = .
∵1.2> >1.1,且y=在[0,+∞)上单调递增,
∴ > > ,即> > .
把本例的各组数据更换如下,再比较其大小关系:
多维探究
(2) 与
幂函数y=x0.5在[0,+∞)上单调递增,
又> ,
所以> .
(1) 与
幂函数y=x-1在(-∞,0)上单调递减,
又-<-,
所以> .
比较幂的大小时
若指数相同,则利用幂函数的单调性比较大小;
若底数、指数均不同,则考虑用中间值法比较大小,这里的中间值可以是“0”或“1”.
方法总结
随堂检测
1.思考辨析
(1)幂函数的图象都过点(0,0),(1,1).( )
(2)幂函数的图象一定不能出现在第四象限.( )
(3)当幂指数α取1,3,时,幂函数y=xα是增函数.( )
(4)当幂指数α=-1时,幂函数y=xα在定义域上是减函数.( )
×
√
√
×
2.幂函数的图象过点(2,),则该幂函数的解析式是( )
A.y=x-1 B.y=
C.y=x2 D.y=x3
设f(x)=xα,则2α=,
∴α=,∴f(x)= .
B
3.函数y=的图象是( )
A B C D
C
4.比较下列各组数的大小:
(1) 与; (2) , , .
函数y= 在(0,+∞)上为减函数,
又3<3.1,
所以> .
> =1,
0< < =1
<0
所以> > .
1.判断一个函数是否为幂函数,其关键是判断其是否符合y=xα(α为常数)的形式.
2.幂函数的图象是幂函数性质的直观反映,会用类比的思想分析函数y=xα(α为常数)同五个函数(y=x,y=x2,y=x3,y=x-1,y= )图象与性质的关系.
3.幂函数的单调性是比较幂值大小关系的重要依据,要学会用幂函数的图象及性质处理幂值大小的比较问题.
本课小结
通过本节课,你学会了什么?
幂函数
1.了解幂函数的概念,会求幂函数的解析式.
2.结合y=x,y=x2,y=x3,y= ,y=x-1的图象,了解它们的变化情况.
3.能利用幂函数的单调性比较指数幂的大小.
本节目标
课前预习
(1)幂函数是如何定义的?
(2)幂函数的解析式具有什么特点?
(3)常见幂函数的图象是什么?它具有哪些性质?
预习课本P89~91,思考并完成以下问题
课前小测
1.下列函数中不是幂函数的是( )
A.y= B.y=x3
C.y=3x D.y=x-1
C
不符合幂函数y=xα的形式
2.已知f(x)=(m+1) 是幂函数,则m=( )
A.2 B.1 C.3 D.0
m+1=1,即m=0
D
3.已知幂函数f(x)=xα的图象过点,则f(4)=________.
f(2)=
2α=
α=-
f(4)= =
新知探究
1.幂函数的概念
一般地,函数_________叫做幂函数,其中____是自变量,_____是常数.
y=xα
x
α
2.幂函数的图象
在同一平面直角坐标系中,画出幂函数y=x,y=x2,y=x3,y=,y=x-1的图象如图所示:
3.幂函数的性质
y=x y=x2 y=x3 y= y=x-1
定义域 R R R [0,+∞) {x|x≠0}
值域 R [0,+∞) R [0,+∞) {y|y≠0}
奇偶性 奇 偶 奇 非奇非偶 奇
单调性 增函数 x∈[0,+∞) 时,增函数 x∈(-∞,0] 时,减函数 增函数 增函数 x∈(0,+∞)
时,减函数
x∈(-∞,0)
时,减函数
题型突破
典例深度剖析 重点多维探究
题型一 幂函数的概念
[例1] 已知y=(m2+2m-2) +2n-3是幂函数,求m,n的值.
所以m=-3,n= .
由题意得
解得
判断一个函数是否为幂函数的依据是该函数是否为y=xα α为常数 的形式,即函数的解析式为一个幂的形式,且需满足:
1 指数为常数;
2 底数为自变量;
3 系数为1.
判断一个函数是否为幂函数的方法
方法总结
1.在函数y=,y=2x2,y=x2+x,y=1中,幂函数的个数为( )
A.0 B.1
C.2 D.3
跟踪训练
B
√
×
×
×
题型二 幂函数的图象及应用
[例2] 点(,2)与点分别在幂函数f(x),g(x)的图象上,问当x为何值时,有:
(1)f(x)>g(x); (2)f(x)=g(x); (3)f(x)
(1)f(x)>g(x); (2)f(x)=g(x); (3)f(x)
∵()α=2,(-2)β=- ,
∴α=2,β=-1,
∴f(x)=x2,g(x)=x-1.
分别作出它们的图象,如图所示.
[例2] 点(,2)与点分别在幂函数f(x),g(x)的图象上,问当x为何值时,有:
(1)f(x)>g(x); (2)f(x)=g(x); (3)f(x)
(1) 当x∈(-∞,0)∪(1,+∞)时,f(x)>g(x);
(2) 当x=1时,f(x)=g(x);
(3) 当x∈(0,1)时,f(x)
在 0,1 上,指数越大,幂函数图象越靠近x轴 简记为指大图低 ;
在 1,+∞ 上,指数越大,幂函数图象越远离x轴 简记为指大图高 .
解决幂函数图象问题应把握的两个原则
②依据图象确定幂指数α与0,1的大小关系,即根据幂函数在第一象限内的图象 类似于y=x-1或y=或y=x3 来判断.
方法总结
2. (1)若四个幂函数y=xa,y=xb,y=xc,y=xd在同一坐标系中的图象如图,则a,b,c,d的大小关系是( )
A.d>c>b>a B.a>b>c>d
C.d>c>a>b D.a>b>d>c
跟踪训练
B
(2)函数y=-1的图象关于x轴对称的图象大致是( )
A B C D
B
y=的图象位于第一象限且为增函数,所以函数图象是上升的
y=-1的图象可看作由y=的图象向下平移一个单位得到的(如选项A中的图所示)
将y=-1的图象关于x轴对称后即为选项B
题型三 幂函数性质的综合应用
[探究问题]
1.幂函数y=xα在(0,+∞)上的单调性与α有什么关系?
提示:
当α>0时,幂函数y=xα在(0,+∞)上单调递增;当α<0时,幂函数y=xα在(0,+∞)上单调递减.
2.2.3-0.2和2.2-0.2可以看作哪一个函数的两个函数值?二者的大小关系如何?
提示:
2.3-0.2和2.2-0.2可以看作幂函数f(x)=x-0.2的两个函数值,因为函数f(x)=x-0.2在(0,+∞)上单调递减,所以2.3-0.2<2.2-0.2.
[探究问题]
[例3] 比较下列各组中幂值的大小:
(1) 0.213, 0.233; (2) , , .
∵函数y=x3是增函数,且0.21<0.23,
∴0.213<0.233.
[例3] 比较下列各组中幂值的大小:
(1) 0.213, 0.233; (2) , , .
= , = .
∵1.2> >1.1,且y=在[0,+∞)上单调递增,
∴ > > ,即> > .
把本例的各组数据更换如下,再比较其大小关系:
多维探究
(2) 与
幂函数y=x0.5在[0,+∞)上单调递增,
又> ,
所以> .
(1) 与
幂函数y=x-1在(-∞,0)上单调递减,
又-<-,
所以> .
比较幂的大小时
若指数相同,则利用幂函数的单调性比较大小;
若底数、指数均不同,则考虑用中间值法比较大小,这里的中间值可以是“0”或“1”.
方法总结
随堂检测
1.思考辨析
(1)幂函数的图象都过点(0,0),(1,1).( )
(2)幂函数的图象一定不能出现在第四象限.( )
(3)当幂指数α取1,3,时,幂函数y=xα是增函数.( )
(4)当幂指数α=-1时,幂函数y=xα在定义域上是减函数.( )
×
√
√
×
2.幂函数的图象过点(2,),则该幂函数的解析式是( )
A.y=x-1 B.y=
C.y=x2 D.y=x3
设f(x)=xα,则2α=,
∴α=,∴f(x)= .
B
3.函数y=的图象是( )
A B C D
C
4.比较下列各组数的大小:
(1) 与; (2) , , .
函数y= 在(0,+∞)上为减函数,
又3<3.1,
所以> .
> =1,
0< < =1
<0
所以> > .
1.判断一个函数是否为幂函数,其关键是判断其是否符合y=xα(α为常数)的形式.
2.幂函数的图象是幂函数性质的直观反映,会用类比的思想分析函数y=xα(α为常数)同五个函数(y=x,y=x2,y=x3,y=x-1,y= )图象与性质的关系.
3.幂函数的单调性是比较幂值大小关系的重要依据,要学会用幂函数的图象及性质处理幂值大小的比较问题.
本课小结
通过本节课,你学会了什么?
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
