人教A版(2019)数学必修第一册 4.1指数(1)课件(共34张PPT)
文档属性
| 名称 | 人教A版(2019)数学必修第一册 4.1指数(1)课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 00:00:00 | ||
图片预览











文档简介
(共34张PPT)
指数(1)
1.理解n次方根及根式的概念,掌握根式的性质.
2.能利用根式的性质对根式进行运算
本节目标
课前预习
(1) n次方根是怎样定义的?
(2) 根式的定义是什么?它有哪些性质?
预习课本P104~105,思考并完成以下问题
课前检测
1. 的运算结果是( )
A.3 B.-3
C.±3 D.±
= =3
A
2.m是实数,则下列式子中可能没有意义的是( )
A. B.
C. D.
C
当m<0时,没有意义
3.下列说法正确的个数是( )
①16的4次方根是2;
② 的运算结果是±2;
③当n为大于1的奇数时,对任意a∈R都有意义;
④当n为大于1的偶数时, 只有当a≥0时才有意义.
A.1 B.2 C.3 D.4
16的4次方根应是±2
=2
B
×
×
√
√
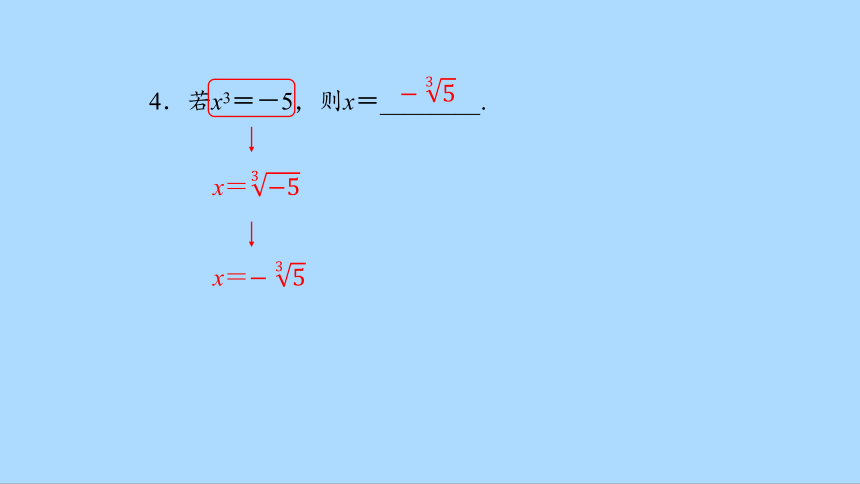
4.若x3=-5,则x=________.
x=
x=
新知探究
1.根式及相关概念
a的n次方根定义
如果______,那么x叫做a的n次方根,其中n>1,且n∈N*.
xn=a
a的n次方根的表示
n的奇偶性 a的n次方根的表示符号 a的取值范围
n为奇数 R
n为偶数 ± [0,+∞)
根式
式子叫做根式,这里n叫做_________,a叫做__________.
根指数
被开方数
2.根式的性质(n>1,且n∈N*)
(1)n为奇数时,=_______.
(2)n为偶数时, =______=____________.
(3) =_______.
(4)负数没有_________方根.
a
|a|
0
偶次
思考:()n中实数a的取值范围是任意实数吗?
提示:不一定,当n为大于1的奇数时,a∈R;
当n为大于1的偶数时,a≥0.
题型突破
典例深度剖析 重点多维探究
题型一 n次方根的概念问题
[例1] (1)27的立方根是________.
(2)已知x6=2019,则x=________.
(3)若有意义,则实数x的取值范围为__________.
3
x+3≥0
[-3,+∞)
x≥-3
1 n的奇偶性决定了n次方根的个数;
2 n为奇数时,a的正负决定着n次方根的符号.
方法总结
n次方根的个数及符号的确定
跟踪训练
1.已知a∈R,n∈N*,给出下列4个式子:
① ;② ;③ ;④ ,其中无意义的有( )
A.1个 B.2个 C.3个 D.0个
有意义
有意义
无意义
有意义
A
题型二 利用根式的性质化简求值
[例2] 化简下列各式
(1) +()5;
(2) +()6;
(3) .
原式=|x+2|=
原式=(-2)+(-2)=-4.
原式=|-2|+2=2+2=4.
① ()n已暗含了有意义,据n的奇偶性可知a的范围;
正确区分与()n
易错提示
②中的a可以是全体实数, 的值取决于n的奇偶性.
跟踪训练
2.若=3a-1,求a的取值范围.
∵ = =|3a-1|,
由|3a-1|=3a-1可知3a-1≥0,∴a≥ .
故a的取值范围为.
题型三 有限制条件的根式的运算
[探究问题]
1.当a>b时,等于多少?
提示:当a>b时, =a-b.
题型三 有限制条件的根式的运算
[探究问题]
2.|a|的代数意义是什么?
提示:|a|=
[例3] (1)若x<0,则x+|x|+ =________.
(2)若-3[例3] (1)若x<0,则x+|x|+ =________.
∵x<0
∴|x|=-x, =|x|=-x
∴x+|x|+=x-x-1=-1
-1
[例3] (2)若-3当-3当1因此,原式=
-
= - =|x-1|-|x+3|,
多维探究
变式1 (1)若x<0,则+ =________.
+ = x +
= x +1
x +1
多维探究
变式2 (2)若x≤-3,求- 的值.
原式= -=|x-1|-|x+3|.
因为x≤-3,所以x-1<0,x+3≤0,
所以原式=-(x-1)+(x+3)=4.
1 有条件根式的化简问题,是指被开方数或被开方的表达式可以通过配方、拆分等方式进行化简.
2 有条件根式的化简经常用到配方的方法.当根指数为偶数时,在利用公式化简时,要考虑被开方数或被开方的表达式的正负.
带条件根式的化简
技法点拨
随堂检测
1.思考辨析
(1)实数a的奇次方根只有一个.( )
(2)当n∈N*时,()n=-2.( )
(3) =π-4.( )
√
×
×
2.已知m10=2,则m等于( )
A. B.-
C. D.±
D
∵m10=2,∴m是2的10次方根.
又∵10是偶数,
∴2的10次方根有两个,且互为相反数.
∴m=±.
3. =________.
= 4-π+π-3=1
1
4.已知-1原式= - =|x-2|-|x+1|.
因为-1所以x+1>0,x-2<0,
所以原式=2-x-x-1=1-2x.
1.注意同()n的区别.前者求解时,要分n为奇数还是偶数,同时要注意实数a的正负,而后者()n=a是恒等式,只要()n有意义,其值恒等于a.
本课小结
2.一个数到底有没有n次方根,我们一定先考虑被开方数到底是正数还是负数,还要分清n为奇数或偶数这两种情况.
通过本节课,你学会了什么?
指数(1)
1.理解n次方根及根式的概念,掌握根式的性质.
2.能利用根式的性质对根式进行运算
本节目标
课前预习
(1) n次方根是怎样定义的?
(2) 根式的定义是什么?它有哪些性质?
预习课本P104~105,思考并完成以下问题
课前检测
1. 的运算结果是( )
A.3 B.-3
C.±3 D.±
= =3
A
2.m是实数,则下列式子中可能没有意义的是( )
A. B.
C. D.
C
当m<0时,没有意义
3.下列说法正确的个数是( )
①16的4次方根是2;
② 的运算结果是±2;
③当n为大于1的奇数时,对任意a∈R都有意义;
④当n为大于1的偶数时, 只有当a≥0时才有意义.
A.1 B.2 C.3 D.4
16的4次方根应是±2
=2
B
×
×
√
√
4.若x3=-5,则x=________.
x=
x=
新知探究
1.根式及相关概念
a的n次方根定义
如果______,那么x叫做a的n次方根,其中n>1,且n∈N*.
xn=a
a的n次方根的表示
n的奇偶性 a的n次方根的表示符号 a的取值范围
n为奇数 R
n为偶数 ± [0,+∞)
根式
式子叫做根式,这里n叫做_________,a叫做__________.
根指数
被开方数
2.根式的性质(n>1,且n∈N*)
(1)n为奇数时,=_______.
(2)n为偶数时, =______=____________.
(3) =_______.
(4)负数没有_________方根.
a
|a|
0
偶次
思考:()n中实数a的取值范围是任意实数吗?
提示:不一定,当n为大于1的奇数时,a∈R;
当n为大于1的偶数时,a≥0.
题型突破
典例深度剖析 重点多维探究
题型一 n次方根的概念问题
[例1] (1)27的立方根是________.
(2)已知x6=2019,则x=________.
(3)若有意义,则实数x的取值范围为__________.
3
x+3≥0
[-3,+∞)
x≥-3
1 n的奇偶性决定了n次方根的个数;
2 n为奇数时,a的正负决定着n次方根的符号.
方法总结
n次方根的个数及符号的确定
跟踪训练
1.已知a∈R,n∈N*,给出下列4个式子:
① ;② ;③ ;④ ,其中无意义的有( )
A.1个 B.2个 C.3个 D.0个
有意义
有意义
无意义
有意义
A
题型二 利用根式的性质化简求值
[例2] 化简下列各式
(1) +()5;
(2) +()6;
(3) .
原式=|x+2|=
原式=(-2)+(-2)=-4.
原式=|-2|+2=2+2=4.
① ()n已暗含了有意义,据n的奇偶性可知a的范围;
正确区分与()n
易错提示
②中的a可以是全体实数, 的值取决于n的奇偶性.
跟踪训练
2.若=3a-1,求a的取值范围.
∵ = =|3a-1|,
由|3a-1|=3a-1可知3a-1≥0,∴a≥ .
故a的取值范围为.
题型三 有限制条件的根式的运算
[探究问题]
1.当a>b时,等于多少?
提示:当a>b时, =a-b.
题型三 有限制条件的根式的运算
[探究问题]
2.|a|的代数意义是什么?
提示:|a|=
[例3] (1)若x<0,则x+|x|+ =________.
(2)若-3
∵x<0
∴|x|=-x, =|x|=-x
∴x+|x|+=x-x-1=-1
-1
[例3] (2)若-3
-
= - =|x-1|-|x+3|,
多维探究
变式1 (1)若x<0,则+ =________.
+ = x +
= x +1
x +1
多维探究
变式2 (2)若x≤-3,求- 的值.
原式= -=|x-1|-|x+3|.
因为x≤-3,所以x-1<0,x+3≤0,
所以原式=-(x-1)+(x+3)=4.
1 有条件根式的化简问题,是指被开方数或被开方的表达式可以通过配方、拆分等方式进行化简.
2 有条件根式的化简经常用到配方的方法.当根指数为偶数时,在利用公式化简时,要考虑被开方数或被开方的表达式的正负.
带条件根式的化简
技法点拨
随堂检测
1.思考辨析
(1)实数a的奇次方根只有一个.( )
(2)当n∈N*时,()n=-2.( )
(3) =π-4.( )
√
×
×
2.已知m10=2,则m等于( )
A. B.-
C. D.±
D
∵m10=2,∴m是2的10次方根.
又∵10是偶数,
∴2的10次方根有两个,且互为相反数.
∴m=±.
3. =________.
= 4-π+π-3=1
1
4.已知-1
因为-1
所以原式=2-x-x-1=1-2x.
1.注意同()n的区别.前者求解时,要分n为奇数还是偶数,同时要注意实数a的正负,而后者()n=a是恒等式,只要()n有意义,其值恒等于a.
本课小结
2.一个数到底有没有n次方根,我们一定先考虑被开方数到底是正数还是负数,还要分清n为奇数或偶数这两种情况.
通过本节课,你学会了什么?
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
