人教A版(2019)数学必修第一册 5.5.1两角和与差的正弦、余弦和正切公式(3)课件(共35张PPT)
文档属性
| 名称 | 人教A版(2019)数学必修第一册 5.5.1两角和与差的正弦、余弦和正切公式(3)课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 19:13:35 | ||
图片预览




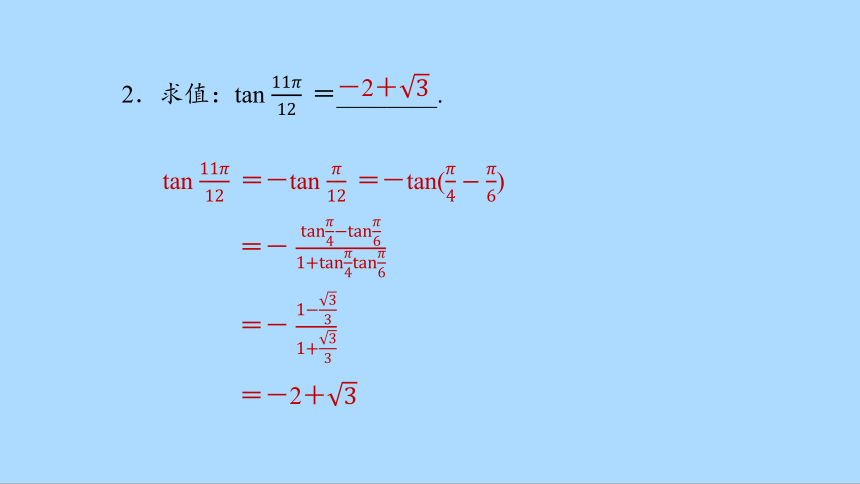
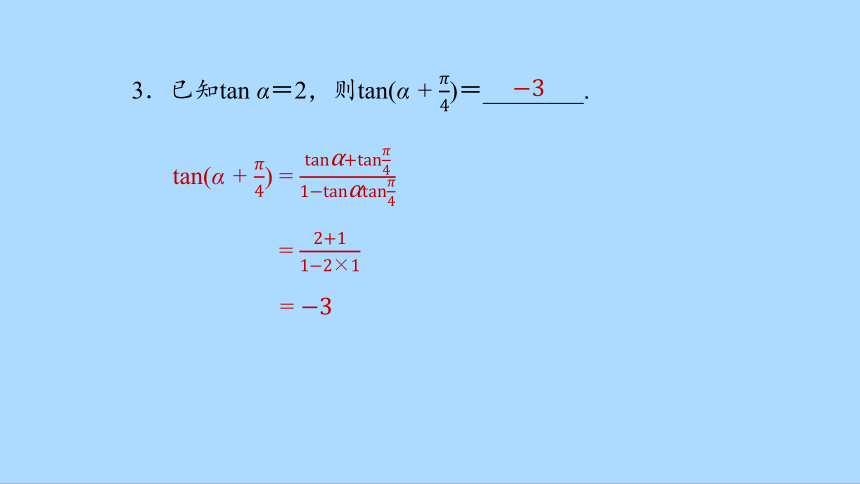
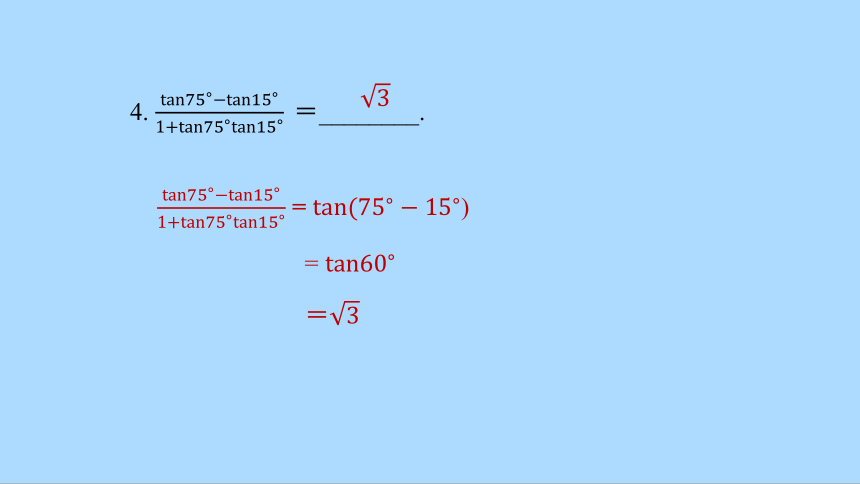





文档简介
(共35张PPT)
两角和与差的正切公式
高一必修第一册
1.能利用两角和与差的正弦、余弦公式推导出两角和与差的正切公式.
2.能利用两角和与差的正切公式进行化简、求值、证明.
本节目标
课前预习
1.tan α,sin α,cos α的关系怎样?利用该关系式及两角和的正、余弦公式,能把tan(α+β)用tan α,tan β表示吗?
预习课本P217~220,思考并完成以下问题
2.怎样用tan α,tan β表示tan(α-β)吗?
课前小测
1.已知tan α+tan β=2,tan(α+β)=4,则tan αtan β等于( )
A.2 B.1 C. D.4
C
∵tan(α+β)= =4,且tan α+tan β=2,
∴ =4,解得tan αtan β= .
2.求值:tan =________.
=-2+
tan =-tan =-tan()
=-
=-
-2+
3.已知tan α=2,则tan(α + )=________.
tan(α + ) =
=
=
4. =________.
= )
=
=
新知探究
cos(αβ)
sin(αβ)
cos(αβ)=cosαcosβ sinαsinβ
sin(αβ)=sinαcos βcosαsin β
两角和与差的正切
tan(αβ)=
=
sinαcos βcosαsin β
cosαcosβ sinαsinβ
=
sinαcosβ
cosαcosβ
cosαsinβ
cosαcosβ
cosαcosβ
cosαcosβ
sinαsinβ
cosαcosβ
=
tanα tanβ
1 tanαtanβ
两角和与差的正切
tan(αβ)=
tanα tanβ
1 tanαtanβ
tan(αβ)=
tan[αβ)]
tanα tan(β)
1 tanαtan (β)
=
tanα tanβ
1 tanαtanβ
=
两角和与差的正切公式
题型突破
典例深度剖析 重点多维探究
题型一 两角和与差的正切公式的正用
[例1] (1)已知α,β均为锐角,tan α= ,tan β= ,则α+β=________.
∵α,β均为锐角,
∵tan α= ,tan β=,
∴tan(α+β)= = =1.
∴α+β∈(0,π),
∴α+β= .
[例1] (2)如图,在△ABC中,AD⊥BC,D为垂足,AD在△ABC的外部,且BD∶CD∶AD=2∶3∶6,则tan∠BAC=________.
∴tan∠BAD= = ,tan∠CAD= = ,
tan∠BAC=tan(∠CAD-∠BAD)
=
=
=
∵AD⊥BC且BD∶CD∶AD=2∶3∶6,
(1)结构特征
公式T(α±β)的右侧为分式形式,其中分子为tan α与tan β的和或差,分母为1与tan αtan β的差或和.
公式T(α±β)的结构特征和符号规律
归纳总结
(2)符号规律
分子同,分母反.
(1)计算待求角的正切值.
(2)缩小待求角的范围,特别注意隐含的信息.
(3)根据角的范围及三角函数值确定角.
利用公式T(α+β)求角的步骤
归纳总结
跟踪训练
1.(1)已知tan(α- )= ,则tan α=________.
=
因为tan(α- )= ,
所以tan α=tan(α - + )
=
=
1.(2)已知角α,β均为锐角,且cos α= ,tan(α-β)=- ,则tan β=________.
所以tan β=tan[α-(α-β)]
因为cos α=,α为锐角,所以sin α= ,tan α= ,
=
=
=3
3
题型二 两角和与差的正切公式的逆用
[例2] (1) =________.
(2) =________.
原式=
=tan(45°+15°)
=tan 60°
=
原式=
=
=tan(-)
=-tan 45°
=-1
-1
要特别注意tan(+α)= , tan(α)= .
归纳总结
公式T α±β 的逆用
一方面要熟记公式的结构,另一方面要注意常值代换.
如 =1, = , =等.
跟踪训练
2.已知α、β均为锐角,且sin 2α=2sin 2β,则( )
A.tan(α+β)=3tan(α-β) B.tan(α+β)=2tan(α-β)
C.3tan(α+β)=tan(α-β) D.3tan(α+β)=2tan(α-β)
∴sin(α+β)cos(α-β)+cos(α+β)sin(α-β)
=2sin(α+β)cos(α-β)-2cos(α+β)sin(α-β),
∴sin(α+β)cos(α-β)=3cos(α+β)sin(α-β),
两边同除以cos(α-β)cos(α+β)得tan(α+β)=3tan(α-β).
∵sin 2α=2sin 2β,
∴sin[(α+β)+(α-β)]=2sin[(α+β)-(α-β)],
A
题型三 两角和与差的正切公式的变形运用
[探究问题]
1.两角和与差的正切公式揭示了tan αtan β与哪些式子的关系?
提示:揭示了tan αtan β与tan α+tan β,tan αtan β与tan α-tan β之间的关系.
2.若tan α、tan β是关于x的方程ax2+bx+c=0(a≠0,b2-4ac≥0)的两个根,则如何用a、b、c表示tan(α+β)
提示:tan(α+β)== =.
[例3] (1)tan 67°-tan 22°-tan 67°tan 22°=________.
∵tan 67°-tan 22°
=tan(67°-22°)(1+tan 67°tan 22°)
=tan 45°(1+tan 67°tan 22°)
=1+tan 67°tan 22°,
∴tan 67°-tan 22°-tan 67°tan 22°
=1+tan 67°tan 22°-tan 67°tan 22°
=1
1
[例3] (2)已知△ABC中,tan B+tan C+ tan Btan C=,且tan A+ tan B=tan Atan B-1,试判断△ABC的形状.
∵ tan A+ tan B=tan Atan B-1,
∴ (tan A+tan B)=tan Atan B-1,
∴ =-,∴tan(A+B)=-.
又0<A+B<π,∴A+B= ,∴C=.
∵tan B+tan C+ tan Btan C=,tan C=,
∴tan B++tan B=,tan B=,
∴B=,∴A= ,∴△ABC为等腰钝角三角形.
多维探究
变式1 tan 68°-tan 23°-tan 68°tan 23°=________.
即tan 68°-tan 23°-tan 68°tan 23°=1.
∵tan 45°=tan(68°-23°)= ,
∴1+tan 68°tan 23°=tan 68°-tan 23°,
1
变式2 能否为例3(1)和变式1归纳出一个一般结论?若能,试证明.
一般结论
若α-β=45°(α,β≠k×180°+90°,k∈Z),则tan α-tan β-tan αtan β=1.
证明
∵tan 45°=tan(α-β)= ,
∴1+tan αtan β=tan α-tan β,
即tan α-tan β-tan αtan β=1.
1.整体意识
若化简的式子中出现了“tan α±tan β”及“tan α·tan β”两个整体,常考虑tan(α±β)的变形公式.
2.熟知变形
两角和的正切公式的常见四种变形:
(1)tan α+tan β=tan(α+β)(1-tan αtan β);
(2)1-tan αtan β= ;
(3)tan α+tan β+tan α·tan β·tan(α+β)=tan(α+β);
(4)tan α·tan β=1-.
技法点拨
随堂检测
1.思考辨析
(1)存在α,β∈R,使tan(α+β)=tan α+tan β成立.( )
(2)对任意α,β∈R,tan(α+β)= 都成立.( )
(3)tan(α+β)=等价于tanα+tanβ=tan(α+β)·(1-tanαtanβ).( )
当α=0,β=时成立
√
α,β,α+β≠kπ+ (k∈Z)
×
√
2.若tan β=3,tan(α-β)=-2,则tan α=( )
A. B. - C.1 D.-1
tan α=tan[(α-β)+β]
=
=
=
A
3.若tan()=3,则tan α的值为________.
tan α=tan[]
=
=
=
4.已知cos α=,cos β= ,其中α,β都是锐角,求tan(α+β)的值.
因为α,β都是锐角,
所以sin α= = ,
sin β= = ,
tan α= =2,tan β= = ,
所以tan(α+β)= =-2.
2.注意公式的变形应用.
如:tan α+tan β=tan(α+β)(1-tan αtan β),
1-tan αtan β= ,
tan α-tan β=tan(α-β)(1+tan αtan β),
1+tan αtan β= 等.
1.公式T(α±β)与S(α±β)、C(α±β)的一个重要区别,就是前者角α、β、α±β都不能取kπ+(k∈Z),而后两者α、β∈R,应用时要特别注意这一点.
本课小结
通过本节课,你学会了什么?
两角和与差的正切公式
高一必修第一册
1.能利用两角和与差的正弦、余弦公式推导出两角和与差的正切公式.
2.能利用两角和与差的正切公式进行化简、求值、证明.
本节目标
课前预习
1.tan α,sin α,cos α的关系怎样?利用该关系式及两角和的正、余弦公式,能把tan(α+β)用tan α,tan β表示吗?
预习课本P217~220,思考并完成以下问题
2.怎样用tan α,tan β表示tan(α-β)吗?
课前小测
1.已知tan α+tan β=2,tan(α+β)=4,则tan αtan β等于( )
A.2 B.1 C. D.4
C
∵tan(α+β)= =4,且tan α+tan β=2,
∴ =4,解得tan αtan β= .
2.求值:tan =________.
=-2+
tan =-tan =-tan()
=-
=-
-2+
3.已知tan α=2,则tan(α + )=________.
tan(α + ) =
=
=
4. =________.
= )
=
=
新知探究
cos(αβ)
sin(αβ)
cos(αβ)=cosαcosβ sinαsinβ
sin(αβ)=sinαcos βcosαsin β
两角和与差的正切
tan(αβ)=
=
sinαcos βcosαsin β
cosαcosβ sinαsinβ
=
sinαcosβ
cosαcosβ
cosαsinβ
cosαcosβ
cosαcosβ
cosαcosβ
sinαsinβ
cosαcosβ
=
tanα tanβ
1 tanαtanβ
两角和与差的正切
tan(αβ)=
tanα tanβ
1 tanαtanβ
tan(αβ)=
tan[αβ)]
tanα tan(β)
1 tanαtan (β)
=
tanα tanβ
1 tanαtanβ
=
两角和与差的正切公式
题型突破
典例深度剖析 重点多维探究
题型一 两角和与差的正切公式的正用
[例1] (1)已知α,β均为锐角,tan α= ,tan β= ,则α+β=________.
∵α,β均为锐角,
∵tan α= ,tan β=,
∴tan(α+β)= = =1.
∴α+β∈(0,π),
∴α+β= .
[例1] (2)如图,在△ABC中,AD⊥BC,D为垂足,AD在△ABC的外部,且BD∶CD∶AD=2∶3∶6,则tan∠BAC=________.
∴tan∠BAD= = ,tan∠CAD= = ,
tan∠BAC=tan(∠CAD-∠BAD)
=
=
=
∵AD⊥BC且BD∶CD∶AD=2∶3∶6,
(1)结构特征
公式T(α±β)的右侧为分式形式,其中分子为tan α与tan β的和或差,分母为1与tan αtan β的差或和.
公式T(α±β)的结构特征和符号规律
归纳总结
(2)符号规律
分子同,分母反.
(1)计算待求角的正切值.
(2)缩小待求角的范围,特别注意隐含的信息.
(3)根据角的范围及三角函数值确定角.
利用公式T(α+β)求角的步骤
归纳总结
跟踪训练
1.(1)已知tan(α- )= ,则tan α=________.
=
因为tan(α- )= ,
所以tan α=tan(α - + )
=
=
1.(2)已知角α,β均为锐角,且cos α= ,tan(α-β)=- ,则tan β=________.
所以tan β=tan[α-(α-β)]
因为cos α=,α为锐角,所以sin α= ,tan α= ,
=
=
=3
3
题型二 两角和与差的正切公式的逆用
[例2] (1) =________.
(2) =________.
原式=
=tan(45°+15°)
=tan 60°
=
原式=
=
=tan(-)
=-tan 45°
=-1
-1
要特别注意tan(+α)= , tan(α)= .
归纳总结
公式T α±β 的逆用
一方面要熟记公式的结构,另一方面要注意常值代换.
如 =1, = , =等.
跟踪训练
2.已知α、β均为锐角,且sin 2α=2sin 2β,则( )
A.tan(α+β)=3tan(α-β) B.tan(α+β)=2tan(α-β)
C.3tan(α+β)=tan(α-β) D.3tan(α+β)=2tan(α-β)
∴sin(α+β)cos(α-β)+cos(α+β)sin(α-β)
=2sin(α+β)cos(α-β)-2cos(α+β)sin(α-β),
∴sin(α+β)cos(α-β)=3cos(α+β)sin(α-β),
两边同除以cos(α-β)cos(α+β)得tan(α+β)=3tan(α-β).
∵sin 2α=2sin 2β,
∴sin[(α+β)+(α-β)]=2sin[(α+β)-(α-β)],
A
题型三 两角和与差的正切公式的变形运用
[探究问题]
1.两角和与差的正切公式揭示了tan αtan β与哪些式子的关系?
提示:揭示了tan αtan β与tan α+tan β,tan αtan β与tan α-tan β之间的关系.
2.若tan α、tan β是关于x的方程ax2+bx+c=0(a≠0,b2-4ac≥0)的两个根,则如何用a、b、c表示tan(α+β)
提示:tan(α+β)== =.
[例3] (1)tan 67°-tan 22°-tan 67°tan 22°=________.
∵tan 67°-tan 22°
=tan(67°-22°)(1+tan 67°tan 22°)
=tan 45°(1+tan 67°tan 22°)
=1+tan 67°tan 22°,
∴tan 67°-tan 22°-tan 67°tan 22°
=1+tan 67°tan 22°-tan 67°tan 22°
=1
1
[例3] (2)已知△ABC中,tan B+tan C+ tan Btan C=,且tan A+ tan B=tan Atan B-1,试判断△ABC的形状.
∵ tan A+ tan B=tan Atan B-1,
∴ (tan A+tan B)=tan Atan B-1,
∴ =-,∴tan(A+B)=-.
又0<A+B<π,∴A+B= ,∴C=.
∵tan B+tan C+ tan Btan C=,tan C=,
∴tan B++tan B=,tan B=,
∴B=,∴A= ,∴△ABC为等腰钝角三角形.
多维探究
变式1 tan 68°-tan 23°-tan 68°tan 23°=________.
即tan 68°-tan 23°-tan 68°tan 23°=1.
∵tan 45°=tan(68°-23°)= ,
∴1+tan 68°tan 23°=tan 68°-tan 23°,
1
变式2 能否为例3(1)和变式1归纳出一个一般结论?若能,试证明.
一般结论
若α-β=45°(α,β≠k×180°+90°,k∈Z),则tan α-tan β-tan αtan β=1.
证明
∵tan 45°=tan(α-β)= ,
∴1+tan αtan β=tan α-tan β,
即tan α-tan β-tan αtan β=1.
1.整体意识
若化简的式子中出现了“tan α±tan β”及“tan α·tan β”两个整体,常考虑tan(α±β)的变形公式.
2.熟知变形
两角和的正切公式的常见四种变形:
(1)tan α+tan β=tan(α+β)(1-tan αtan β);
(2)1-tan αtan β= ;
(3)tan α+tan β+tan α·tan β·tan(α+β)=tan(α+β);
(4)tan α·tan β=1-.
技法点拨
随堂检测
1.思考辨析
(1)存在α,β∈R,使tan(α+β)=tan α+tan β成立.( )
(2)对任意α,β∈R,tan(α+β)= 都成立.( )
(3)tan(α+β)=等价于tanα+tanβ=tan(α+β)·(1-tanαtanβ).( )
当α=0,β=时成立
√
α,β,α+β≠kπ+ (k∈Z)
×
√
2.若tan β=3,tan(α-β)=-2,则tan α=( )
A. B. - C.1 D.-1
tan α=tan[(α-β)+β]
=
=
=
A
3.若tan()=3,则tan α的值为________.
tan α=tan[]
=
=
=
4.已知cos α=,cos β= ,其中α,β都是锐角,求tan(α+β)的值.
因为α,β都是锐角,
所以sin α= = ,
sin β= = ,
tan α= =2,tan β= = ,
所以tan(α+β)= =-2.
2.注意公式的变形应用.
如:tan α+tan β=tan(α+β)(1-tan αtan β),
1-tan αtan β= ,
tan α-tan β=tan(α-β)(1+tan αtan β),
1+tan αtan β= 等.
1.公式T(α±β)与S(α±β)、C(α±β)的一个重要区别,就是前者角α、β、α±β都不能取kπ+(k∈Z),而后两者α、β∈R,应用时要特别注意这一点.
本课小结
通过本节课,你学会了什么?
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
