初三数学(新人教版)27.2.3相似三角形的周长与面积[上学期]
文档属性
| 名称 | 初三数学(新人教版)27.2.3相似三角形的周长与面积[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 32.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-24 11:28:00 | ||
图片预览

文档简介
第二十七章 相似
27.2.3相似三角形的周长与面积
〔教学目标〕
1. 经历探索相似三角形性质的过程,并在探究过程中发展学生积极的情感、态度、价值观,体验解决问题策略的多样性。
2.理解并掌握相似三角形周长的比等于相似比、面积比等于相似比的平方,并能用来解决简单的问题。
3.探索相似多边形周长的比等于相似比、面积比等于相似比的平方,体验化归思想。
〔教学重点与难点〕
重点:理解并掌握相似三角形周长的比等于相似比、面积比等于相似比的平方。
难点:探索相似多边形周长的比等于相似比、面积比等于相似比的平方。
〔教学设计〕
教学过程 设计意图说明
新课引入:1.回顾相似三角形的概念及判定方法。2.复习相似多边形的定义及相似多边形对应边、对应角的性质。 以旧引新,帮助学生建立新旧知识间的联系。
提出问题: 如果两个三角形相似,它们的周长之间什么关系?两个相似多边形呢?(学生小组讨论) ↓ ABC∽ A1B1C1,相似比为kAB=kA1B1,BC=kB1C1,CA=kC1A1相似三角形周长的比等于相似比相似多边形周长的比等于相似比延伸问题: 探究:如图27.2-11(1), ABC∽ A1B1C1,相似比为k1 ,它们的面积比是多少?
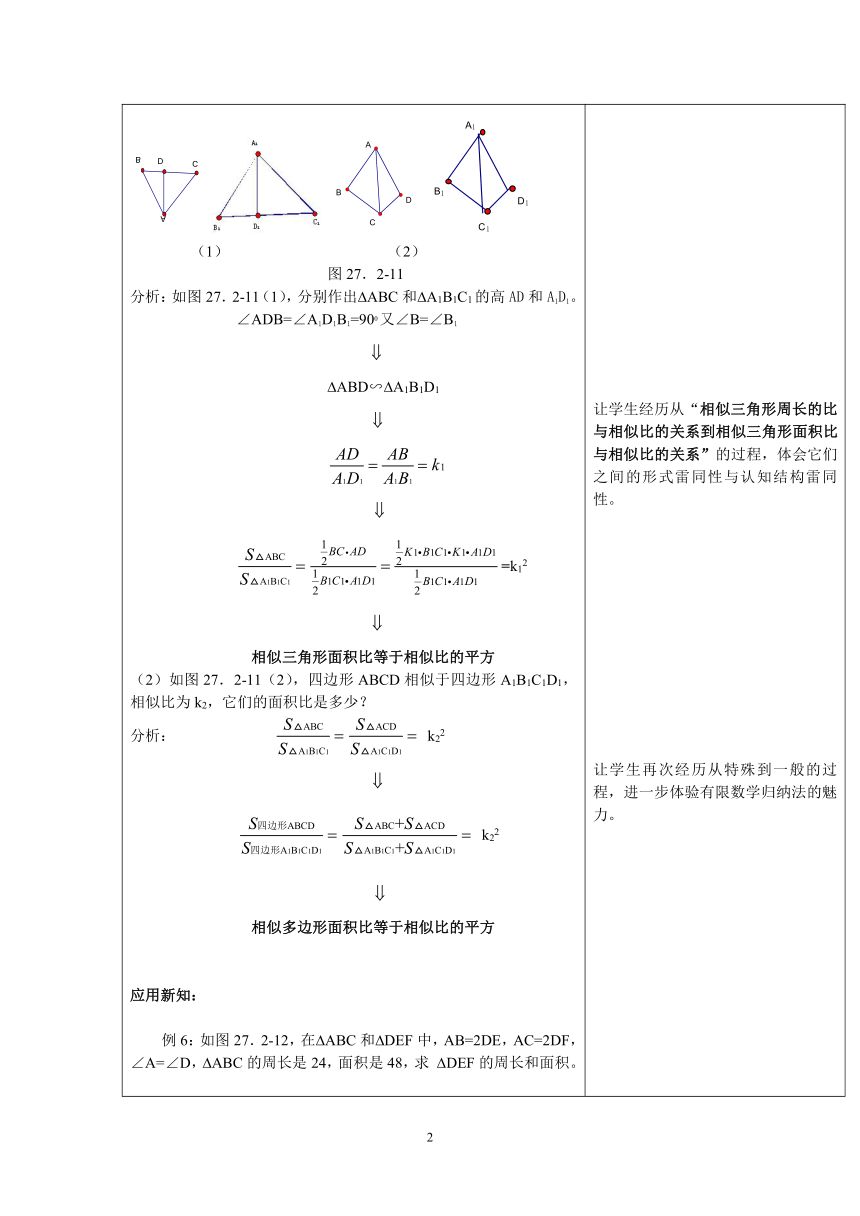
(1) (2)图27.2-11分析:如图27.2-11(1),分别作出 ABC和 A1B1C1的高AD和A1D1。∠ADB=∠A1D1B1=900又∠B=∠B1 ABD∽ A1B1D1=k12相似三角形面积比等于相似比的平方(2)如图27.2-11(2),四边形ABCD相似于四边形A1B1C1D1,相似比为k2,它们的面积比是多少?分析: k22 k22相似多边形面积比等于相似比的平方应用新知:例6:如图27.2-12,在 ABC和 DEF中,AB=2DE,AC=2DF,∠A=∠D, ABC的周长是24,面积是48,求 DEF的周长和面积。图27.2-12分析: ABC和 DEF中,AB=2DE,AC=2DF又∠A=∠D ABC∽ DEF,相似比为 DEF的周长=24=12,面积=248=12。 让学生经历从特殊到一般的过程,体会有限数学归纳法的魅力,学生以小组讨论的形式开展学习有利于丰富学生的探究经验。让学生经历从“相似三角形周长的比与相似比的关系到相似三角形面积比与相似比的关系”的过程,体会它们之间的形式雷同性与认知结构雷同性。让学生再次经历从特殊到一般的过程,进一步体验有限数学归纳法的魅力。让学生了解运用“相似三角形周长的比等于相似比、面积比等于相似比的平方”的常见解题思路。
运用提高:P54练习题1P54练习题2 让学生在练习中熟悉利用相似三角形周长的比等于相似比、面积比等于相似比的平方,解决简单的问题。
课堂小结:说说你在本节课的收获。 让学生及时回顾整理本节课所学的知识。
布置作业:必做题:P54练习题3,4选做题:P57习题27·2题12,13,14。3.备选题:如图,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点(P异于A、D),Q是BC边上的任意一点. 连AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.(1)求证:△APE∽△ADQ;(2)设AP的长为x,试求△PEF的面积S△PEF关于x的函数关系式,并求当P在何处时,S△PEF取得最大值?最大值为多少?(3)当Q在何处时,△ADQ的周长最小?(须给出确定Q在何处的过程或方法,不必给出证明) 分层次布置作业,让不同的学生在本节课中都有收获。备选题答案:(1)证∠APE=∠ADQ,∠AEP=∠AQD.注意到△APE∽△ADQ与△PDE∽△ADQ,及S△PEF=,得S△PEF==. ∴当,即P是AD的中点时,S△PEF取得最大值.(3)作A关于直线BC的对称点A′,连DA′交BC于Q,则这个点Q就是使△ADQ周长最小的点,此时Q是BC的中点.
设计思想:
本节课主要是让学生理解并掌握相似三角形周长的比等于相似比、面积比等于相似比的平方,通过探索相似多边形周长的比等于相似比、面积比等于相似比的平方,体验化归思想,学会应用相似三角形周长的比等于相似比、面积比等于相似比的平方来解决简单的问题。因此本教学设计突出了“相似比相似三角形周长的比相似多边形周长的比”、“相似比相似三角形面积的比相似多边形面积的比”等一系列从特殊到一般的过程,以让学生深刻体验到有限数学归纳法的魅力。
PAGE
4
27.2.3相似三角形的周长与面积
〔教学目标〕
1. 经历探索相似三角形性质的过程,并在探究过程中发展学生积极的情感、态度、价值观,体验解决问题策略的多样性。
2.理解并掌握相似三角形周长的比等于相似比、面积比等于相似比的平方,并能用来解决简单的问题。
3.探索相似多边形周长的比等于相似比、面积比等于相似比的平方,体验化归思想。
〔教学重点与难点〕
重点:理解并掌握相似三角形周长的比等于相似比、面积比等于相似比的平方。
难点:探索相似多边形周长的比等于相似比、面积比等于相似比的平方。
〔教学设计〕
教学过程 设计意图说明
新课引入:1.回顾相似三角形的概念及判定方法。2.复习相似多边形的定义及相似多边形对应边、对应角的性质。 以旧引新,帮助学生建立新旧知识间的联系。
提出问题: 如果两个三角形相似,它们的周长之间什么关系?两个相似多边形呢?(学生小组讨论) ↓ ABC∽ A1B1C1,相似比为kAB=kA1B1,BC=kB1C1,CA=kC1A1相似三角形周长的比等于相似比相似多边形周长的比等于相似比延伸问题: 探究:如图27.2-11(1), ABC∽ A1B1C1,相似比为k1 ,它们的面积比是多少?
(1) (2)图27.2-11分析:如图27.2-11(1),分别作出 ABC和 A1B1C1的高AD和A1D1。∠ADB=∠A1D1B1=900又∠B=∠B1 ABD∽ A1B1D1=k12相似三角形面积比等于相似比的平方(2)如图27.2-11(2),四边形ABCD相似于四边形A1B1C1D1,相似比为k2,它们的面积比是多少?分析: k22 k22相似多边形面积比等于相似比的平方应用新知:例6:如图27.2-12,在 ABC和 DEF中,AB=2DE,AC=2DF,∠A=∠D, ABC的周长是24,面积是48,求 DEF的周长和面积。图27.2-12分析: ABC和 DEF中,AB=2DE,AC=2DF又∠A=∠D ABC∽ DEF,相似比为 DEF的周长=24=12,面积=248=12。 让学生经历从特殊到一般的过程,体会有限数学归纳法的魅力,学生以小组讨论的形式开展学习有利于丰富学生的探究经验。让学生经历从“相似三角形周长的比与相似比的关系到相似三角形面积比与相似比的关系”的过程,体会它们之间的形式雷同性与认知结构雷同性。让学生再次经历从特殊到一般的过程,进一步体验有限数学归纳法的魅力。让学生了解运用“相似三角形周长的比等于相似比、面积比等于相似比的平方”的常见解题思路。
运用提高:P54练习题1P54练习题2 让学生在练习中熟悉利用相似三角形周长的比等于相似比、面积比等于相似比的平方,解决简单的问题。
课堂小结:说说你在本节课的收获。 让学生及时回顾整理本节课所学的知识。
布置作业:必做题:P54练习题3,4选做题:P57习题27·2题12,13,14。3.备选题:如图,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点(P异于A、D),Q是BC边上的任意一点. 连AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.(1)求证:△APE∽△ADQ;(2)设AP的长为x,试求△PEF的面积S△PEF关于x的函数关系式,并求当P在何处时,S△PEF取得最大值?最大值为多少?(3)当Q在何处时,△ADQ的周长最小?(须给出确定Q在何处的过程或方法,不必给出证明) 分层次布置作业,让不同的学生在本节课中都有收获。备选题答案:(1)证∠APE=∠ADQ,∠AEP=∠AQD.注意到△APE∽△ADQ与△PDE∽△ADQ,及S△PEF=,得S△PEF==. ∴当,即P是AD的中点时,S△PEF取得最大值.(3)作A关于直线BC的对称点A′,连DA′交BC于Q,则这个点Q就是使△ADQ周长最小的点,此时Q是BC的中点.
设计思想:
本节课主要是让学生理解并掌握相似三角形周长的比等于相似比、面积比等于相似比的平方,通过探索相似多边形周长的比等于相似比、面积比等于相似比的平方,体验化归思想,学会应用相似三角形周长的比等于相似比、面积比等于相似比的平方来解决简单的问题。因此本教学设计突出了“相似比相似三角形周长的比相似多边形周长的比”、“相似比相似三角形面积的比相似多边形面积的比”等一系列从特殊到一般的过程,以让学生深刻体验到有限数学归纳法的魅力。
PAGE
4
