人教版数学七年级上册 第一章 有理数 有理数的大小比较 第七课时 课件(共20张PPT)
文档属性
| 名称 | 人教版数学七年级上册 第一章 有理数 有理数的大小比较 第七课时 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 661.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 19:25:51 | ||
图片预览







文档简介
(共20张PPT)
第一章 有理数
第7课时 有理数的大小比较
目录
01
本课目标
02
课堂导练
本课目标
1. 会通过代数方法比较两个有理数的大小.
2. 会通过几何方法比较两个有理数的大小.
(1)正数______________0,0______________负数,正数______________负数;
(2)两个负数,绝对值大的______________.
知识点一 通过代数方法比较两个有理数的大小
大于
大于
大于
反而小
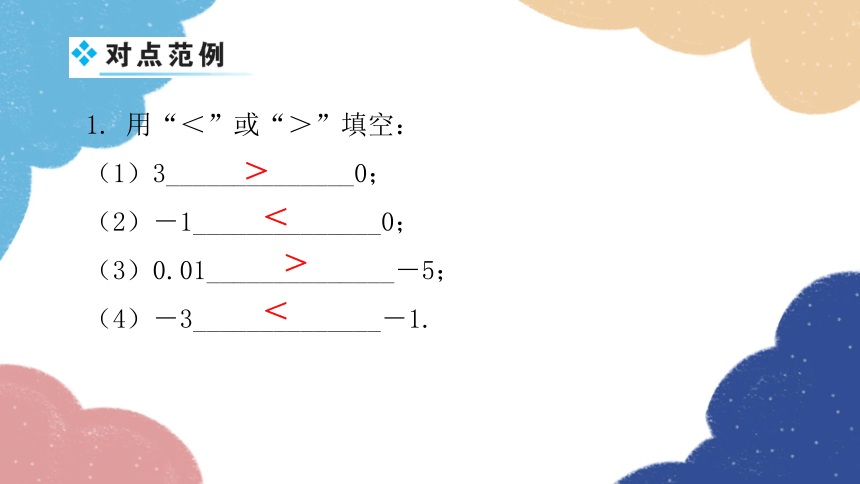
1. 用“<”或“>”填空:
(1)3______________0;
(2)-1______________0;
(3)0.01______________-5;
(4)-3______________-1.
>
<
>
<
知识点二 通过几何方法比较两个有理数的大小
数学上规定,数轴上的点,右边的点所表示的数总比左边的点所表示的数______________.
大
2. 如图1-7-1,数轴上有A,B,C,D四个点,其中表示最大的数的点是______________.
点D
课堂导练
>
>
=
=
思路点拨:(1)两个负数,绝对值大的反而小;(2)有分数时先通分,再比较大小;(3)(4)先化简,再比较大小.
<
<
>
>
<
思路点拨:先化简各数,再在数轴上表示出来,即可得出答案.
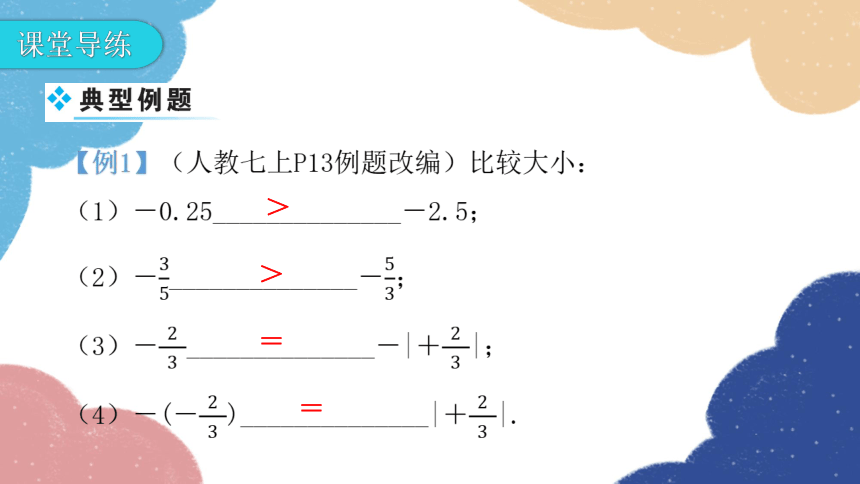
【例3】观察与归纳.
(1)比较下列各式的大小(填“>”“<”或“=”):
①|-2|+|3|______________|-2+3|;
②|-2|+|-3|______________|-2-3|;
③|-2|+|0|______________|-2+0|;
归纳:|a|+|b|______________|a+b|.
(2)根据(1)中得出的结论,若|m|+|n|=9,|m+n|=1,求m的值.
>
=
=
≥
解:由(1)的结论可知,因为|m|+|n|=9,|m+n|=1,|m|+|n|≠|m+n|,所以m,n异号.
当m为正数,n为负数时,m-n=9,则n=m-9,
|m+m-9|=1,m=5或4;
当m为负数,n为正数时,-m+n=9,则n=m+9,
|m+m+9|=1,m=-4或-5.
综上所述,m为±4或±5.
思路点拨:解题的关键是根据绝对值的知识分类讨论解决问题,(1)通过计算找出其中的规律即可得出答案;
(2)根据(1)中的结论分当m为正数,n为负数时和当m为负数,n为正数时两种情况讨论即可确定答案.
3. (1)根据绝对值的定义,利用数轴上两点间的距离比较大小(填“>”“<”或“=”):
①|2|+|6|______________|2-6|;
②|-2|+|3|______________|-2-3|;
③|3|+|-5|______________|3-(-5)|;
④|-2|+|-3|______________|-2-(-3)|;
⑤|0|+|-5|______________|0-(-5)|;
…
>
=
=
>
=
(2)通过(1)分析归纳出当a,b为有理数时,|a|+|b|与|a-b|的大小关系;
解:由(1)可知,
当a,b同号时,|a|+|b|>|a-b|;
当a,b异号时,|a|+|b|=|a-b|;
当a,b中有一个为0时,|a|+|b|=|a-b|.
所以|a|+|b|≥|a-b|.
(3)当|x|+2=|x-2|时,根据(2)中你得出的结论,求x的取值范围.
解:因为|x|+2=|x-2|,
由(2)可知x≤0.
谢 谢
第一章 有理数
第7课时 有理数的大小比较
目录
01
本课目标
02
课堂导练
本课目标
1. 会通过代数方法比较两个有理数的大小.
2. 会通过几何方法比较两个有理数的大小.
(1)正数______________0,0______________负数,正数______________负数;
(2)两个负数,绝对值大的______________.
知识点一 通过代数方法比较两个有理数的大小
大于
大于
大于
反而小
1. 用“<”或“>”填空:
(1)3______________0;
(2)-1______________0;
(3)0.01______________-5;
(4)-3______________-1.
>
<
>
<
知识点二 通过几何方法比较两个有理数的大小
数学上规定,数轴上的点,右边的点所表示的数总比左边的点所表示的数______________.
大
2. 如图1-7-1,数轴上有A,B,C,D四个点,其中表示最大的数的点是______________.
点D
课堂导练
>
>
=
=
思路点拨:(1)两个负数,绝对值大的反而小;(2)有分数时先通分,再比较大小;(3)(4)先化简,再比较大小.
<
<
>
>
<
思路点拨:先化简各数,再在数轴上表示出来,即可得出答案.
【例3】观察与归纳.
(1)比较下列各式的大小(填“>”“<”或“=”):
①|-2|+|3|______________|-2+3|;
②|-2|+|-3|______________|-2-3|;
③|-2|+|0|______________|-2+0|;
归纳:|a|+|b|______________|a+b|.
(2)根据(1)中得出的结论,若|m|+|n|=9,|m+n|=1,求m的值.
>
=
=
≥
解:由(1)的结论可知,因为|m|+|n|=9,|m+n|=1,|m|+|n|≠|m+n|,所以m,n异号.
当m为正数,n为负数时,m-n=9,则n=m-9,
|m+m-9|=1,m=5或4;
当m为负数,n为正数时,-m+n=9,则n=m+9,
|m+m+9|=1,m=-4或-5.
综上所述,m为±4或±5.
思路点拨:解题的关键是根据绝对值的知识分类讨论解决问题,(1)通过计算找出其中的规律即可得出答案;
(2)根据(1)中的结论分当m为正数,n为负数时和当m为负数,n为正数时两种情况讨论即可确定答案.
3. (1)根据绝对值的定义,利用数轴上两点间的距离比较大小(填“>”“<”或“=”):
①|2|+|6|______________|2-6|;
②|-2|+|3|______________|-2-3|;
③|3|+|-5|______________|3-(-5)|;
④|-2|+|-3|______________|-2-(-3)|;
⑤|0|+|-5|______________|0-(-5)|;
…
>
=
=
>
=
(2)通过(1)分析归纳出当a,b为有理数时,|a|+|b|与|a-b|的大小关系;
解:由(1)可知,
当a,b同号时,|a|+|b|>|a-b|;
当a,b异号时,|a|+|b|=|a-b|;
当a,b中有一个为0时,|a|+|b|=|a-b|.
所以|a|+|b|≥|a-b|.
(3)当|x|+2=|x-2|时,根据(2)中你得出的结论,求x的取值范围.
解:因为|x|+2=|x-2|,
由(2)可知x≤0.
谢 谢
